
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Ламинарное течение в трубах.Одномерное течение При движении жидкости по трубам основные изменения скорости и ускорения происходят вдоль оси трубопровода. Изменение параметров вдоль двух других координат можно считать пренебрежимо малыми. Рассмотрим установившееся ламинарное течение жидкости в прямой круглой цилиндрической трубе с внутренним диаметром d=2r0. Чтобы исключить влияние силы тяжести и этим упростить вывод, допустим, что труба расположена горизонтально. Достаточно далеко от входа в нее, где поток уже вполне стабилизировался, выделим отрезок длиной
Пусть в сечении 1-1 давление равно р1, а в сечении 2-2 – р2 . Ввиду постоянства диаметра трубы, скорость жидкости будет постоянной, а коэффициент где Отсюда что и показывают пьезометры, установленные в этих сечениях. В потоке жидкости выделим цилиндрический объем радиусом r, соосный с трубой и имеющий основания в выбранных сечениях. Запишем уравнение равномерного движения выделенного объема жидкости в трубе, т.е. равенство нулю суммы сил, действующих на объем: сил давления и сопротивления. Обозначая касательное напряжение на боковой поверхности цилиндра через Откуда Из формулы следует, что касательные напряжения в поперечном сечении изменяются по линейному закону в функции радиуса. Эпюра касательного напряжения показана на рис. 5.6 слева (эта эпюра не зависит от режима течения).  Выразим касательное напряжение Знак минус обусловлен тем, что направление отсчета r (от оси к стенке) противоположно направлению отсчета у (от стенки). Подставляя значение Найдем отсюда приращение скорости При положительном приращении радиуса получается отрицательное приращение (уменьшение) скорости, что соответствует профилю скоростей, показанному на рис. 5.6. Выполнив интегрирование, получим Постоянную интегрирования С найдем из условия, что на стенке при r = r0, Тогда Скорость по окружности радиусом r равна Это выражение является законом распределения скоростей по сечению круглой трубы при ламинарном течении. Кривая, изображающая эпюру скоростей – парабола второй степени. Максимальная скорость в центре сечения (при r=0) будет Применим полученный закон распределения скоростей, описываемый уравнением (5.5) для расчета расхода. Для этого выразим сначала элементарный расход через бесконечно малую площадку dS Здесь После интегрирования по всей площади поперечного сечения, т.е. от r = 0 до r = r0, получим Среднюю по сечению скорость найдем делением расхода на площадь. С учетом выражения (5.7) получим Сравнение этого выражения с формулой (5.6) показывает, что средняя скорость при ламинарном течении в 2 раза меньше максимальной: Для получения закона сопротивления, т.е. выражения потери напора Разделив это выражение на Полученный закон сопротивления показывает, что при ламинарном течении в трубке круглого сечения потеря напора на трение пропорциональна расходу, длине и вязкости в первой степени и обратно пропорциональна диаметру в четвертой степени. Этот закон (закон Пуазейля), используется для расчета трубопроводов с ламинарным течением. Ранее условились выражать потери напора на трение через среднюю скорость по формуле (5.2). Приведем закон сопротивления (5.9) к виду формулы Вейсбаха – Дарси. Для этого в формуле (5.9) заменим расход выражением или, приведя к виду формулы (5.2), окончательно найдем где Таким образом потеря напора на трение по длине при ламинарном течении пропорциональна скорости в первой степени, а коэффициент Зная закон распределения скоростей по сечению трубы, легко найти коэффициент Корнолиса Коэффициент Кориолиса определяется выражением Расчеты показывают, что Таким образом, кинетическая энергия ламинарного потока в двое больше кинетической энергии, подсчитанной по средней скорости. Изложенная теория ламинарного течения жидкости в круглой трубе хорошо подтверждается опытами.
Турбулентное течение При турбулентном движении осредненная скорость мало меняется по сечению трубопровода. Область, где скорости почти не меняются по сечению, называется ядром течения, а слой у стенок, характеризующийся быстрым уменьшением значения скорости – пристенным слоем, толщина которого весьма мала и составляет доли миллиметра. Равномерное распределение скоростей в ядре объясняется интенсивным перемешиванием масс жидкости, что характерно для турбулентного движения. Экспериментально получена формула для определения распределения скорости по сечению где
Показатель степени n зависит от числа Re для гидравлически гладких труб и от относительной шероховатости для труб вполне шероховатых. Природа касательных напряжений в турбулентном потоке существенно отличается от механизма возникновения касательных напряжений при ламинарном движении. В процессе турбулентного перемешивания массы жидкости из центральной области, обладающие большими скоростями, перемещаются к периферии и наоборот. Если при ламинарном течении потери напора на трение возрастают пропорционально скорости (расходу) в первой степени, то при переходе к турбулентному течению заметны некоторый скачок сопротивления и затем более крутое нарастание величины Ввиду сложности турбулентного течения и трудностей его аналитического исследования, отсутствия достаточно строгой и точной теории, в большинстве случаев для практических расчетов, связанных с турбулентным течением жидкости в трубах, пользуется экспериментальными данными.
Основной расчетной формулой для потерь напора при турбулентном течении в круглых трубах является известная уже формула Вейсбаха – Дарси, имеющая вид Эта основная формула применима как при турбулентном, так и при ламинарном течении; различие лишь заключается в значениях коэффициента Коэффициент где ( Когда шероховатость трубы не влияет на ее сопротивление (на Существует ряд имперических формул для определения применяемая при Re от Reкр до Re, равного нескольким миллионным. При 2300 < Re < 105 можно пользоваться формулой Блазиуса Трубы, в которых коэффициент гидравлического трения Область движения, в которой То есть Характер влияния этих двух параметров на сопротивление труб отчетливо виден из графика (Рис. 5.8), полученного Н.Н. Никурадзе. Никурадзе Н.Н. испытал на сопротивление ряд труб с искусственно созданной шероховатостью на их внутренней поверхности. Испытания были проведены, при широком диапазоне относительных шероховатостей
Штриховыми линиями показаны кривые для труб с различной относительной шероховатостью Рис.5.8.
Из рассмотрения графика можно сделать следующие основные выводы: 1. При ламинарном течении шероховатость на сопротивление не влияет; штриховые линии практически совпадают с прямой А. 2. Критическое число Re от шероховатости практически не зависит; штриховые кривые отклоняются от прямой А приблизительно при одном и том же Reкр ( 3. В области турбулентного течения, но при небольших Re и 4. При больших Re и больших относительных шероховатостях коэффициент Для расчетов
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 292. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 между сечениями 1-1 и 2-2 (рис. 5.6).
между сечениями 1-1 и 2-2 (рис. 5.6). Рис. 5.6. К теории ламинарного течения жидкости в трубе.
Рис. 5.6. К теории ламинарного течения жидкости в трубе. будет неизменным вдоль потока вследствие его стабильности, поэтому уравнение Бернулли для выбранных сечений примет вид
будет неизменным вдоль потока вследствие его стабильности, поэтому уравнение Бернулли для выбранных сечений примет вид ,
, - потеря напора на трение по длине.
- потеря напора на трение по длине. ,
, , получим
, получим .
. .
.
 .
. .
.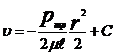 .
.
 .
.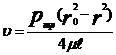 . (5.5)
. (5.5) (5.6)
(5.6) .
. есть функция радиуса, определяемая формулой (5.5), а площадку dS целесообразно взять в виде кольца радиуса r и шириной dr, тогда
есть функция радиуса, определяемая формулой (5.5), а площадку dS целесообразно взять в виде кольца радиуса r и шириной dr, тогда .
. (5.7)
(5.7) . (5.8)
. (5.8) .
. из формулы (5.7)
из формулы (5.7) .
.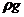 , заменив
, заменив  на
на  и
и  на
на  , а также перейдя от r0 к d = 2 r0, получим
, а также перейдя от r0 к d = 2 r0, получим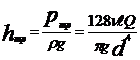 . (5.9)
. (5.9) .
. ; умножив и разделив на
; умножив и разделив на  и перегруппировав множители, после сокращения получим
и перегруппировав множители, после сокращения получим
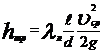 , (5.10)
, (5.10) - коэффициент потерь на трение для ламинарного течения:
- коэффициент потерь на трение для ламинарного течения: . (5.11)
. (5.11) .
. , (5.12)
, (5.12) - max скорость на оси трубопровода.
- max скорость на оси трубопровода. Рис. 5.7. Зависимость
Рис. 5.7. Зависимость  , где
, где  - коэффициент потерь на трение при турбулентном течении.
- коэффициент потерь на трение при турбулентном течении. .
.
 (к) – средняя высота бугорков шероховатости, d – диаметр трубы.
(к) – средняя высота бугорков шероховатости, d – диаметр трубы.
 , (5.13)
, (5.13) . (5.14)
. (5.14) . (5.15)
. (5.15) называют переходной (область смешанного трения)
называют переходной (область смешанного трения) , а также чисел Re
, а также чисел Re  . Результаты этих испытаний представлены на рис. 5.8.
. Результаты этих испытаний представлены на рис. 5.8. Наклонные прямые А и В соответствуют законам сопротивления гладких труб, т.е. формулам (5.11) и (5.14)
Наклонные прямые А и В соответствуют законам сопротивления гладких труб, т.е. формулам (5.11) и (5.14) .
. ).
). шероховатость на сопротивление не влияет; штриховые линии на некоторых участках совпадают и прямой В.
шероховатость на сопротивление не влияет; штриховые линии на некоторых участках совпадают и прямой В. в явном виде
в явном виде , (5.15а)
, (5.15а) - эквивалентная шероховатость, учитывает не только среднюю высоту выступов, но и их форму.
- эквивалентная шероховатость, учитывает не только среднюю высоту выступов, но и их форму.