
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Расчёт уставок линейных выключателей. Проверка тяговой сети на малые токи короткого замыканияМаксимальный ток линии (кабеля) при двухстороннем питании
где
Ток уставки ВАБа принимается равным (1,15-1,2)
где
для схемы выпрямления с нулем
где отношение общего числа вводов высокого напряжения на тяговой подстанции к наименьшему числу работающих вводов на ТП,
Далее проверяется неравенство
1160 А > 664,35 A, 
1028 A > 718,875 A,
923 A > 800,037 A. Таким образом, условие проверки на малый ток в пределах секций короткого замыкания в наиболее удалённых от ТП точках выполняется. Токи кз вблизи секционных изоляторов не являются малыми, и дополнительной защиты тяговой сети от малых токов короткого замыкания не требуется.
Исходные данные для статистического метода расчёта тяговой сети Исходными данными для расчёта являются тяговые нагрузки в положительной питающей линии в виде ряда случайных величин ПЛ, как показания амперметра, присоединённого через шунт в положительную питающую линию. IПЛ Таблица 2. Выборка
Таблица 3- Упорядоченный статистический ряд по возрастанию
Построение гистограммы и эмпирической функции распределения Для выборки объёмом n = 10 число интервалов, на которое разбивается статистический ряд от Iпл min = 80 до Iпл max = 200 q = 3.32lgn + 1 q = 3,32lg10+1 = 4,32 ≈ 4 Длина интервала
Подсчёт количества значений выборки, попавших в каждый интервал, учитывается так, что левая граница каждого интервала принадлежит этому интервалу, а правая – не принадлежит. Составляется таблица для построения гистограммы.
По данным таблицы 3 строится эмпирическая функция распределения
Рисунок 4 - Эмпирическая функция распределения Рисунок 5 - Гистограмма плотности относительных частот |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 383. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

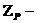 функция вероятности
функция вероятности  ;
; ,
, 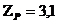 .
.
 А,
А,
 А,
А,
 А.
А.

 А,
А,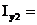
 А,
А,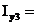
 А.
А. Минимальный ток короткого замыкания в удалённой от подстанции точке
Минимальный ток короткого замыкания в удалённой от подстанции точке
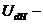 номинальное напряжение преобразовательного агрегата на тяговой подстанции,
номинальное напряжение преобразовательного агрегата на тяговой подстанции,  = 600 В;
= 600 В;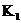 - коэффициент, учитывающий потери напряжения в трансформаторе преобразовательного агрегата
- коэффициент, учитывающий потери напряжения в трансформаторе преобразовательного агрегата 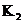 - коэффициент, учитывающий потери напряжения в высоковольтной сети,
- коэффициент, учитывающий потери напряжения в высоковольтной сети, 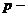 допустимое отклонение питающего ТП напряжения, р = ± 0,05;
допустимое отклонение питающего ТП напряжения, р = ± 0,05; потери напряжения в вентилях выпрямителя,
потери напряжения в вентилях выпрямителя,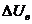 = 5 В;
= 5 В;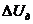 - потери напряжения в электрической дуге,
- потери напряжения в электрической дуге, 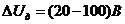 ;
; номинальный ток преобразовательного агрегата на тяговой подстанции;
номинальный ток преобразовательного агрегата на тяговой подстанции;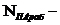 число параллельно работающих преобразовательных агрегатов на тяговой подстанции;
число параллельно работающих преобразовательных агрегатов на тяговой подстанции;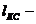 расстояние от положительного питающего пункта на секции контактной сети до наиболее удалённой точки кз в той же секции контактной сети;
расстояние от положительного питающего пункта на секции контактной сети до наиболее удалённой точки кз в той же секции контактной сети;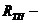 приведённое сопротивление тяговой подстанции, рассчитывается по формуле
приведённое сопротивление тяговой подстанции, рассчитывается по формуле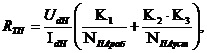
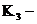 коэффициент, учитывающий число одновременно работающих вводов на тяговой подстанции в момент кз, рассчитывается как
коэффициент, учитывающий число одновременно работающих вводов на тяговой подстанции в момент кз, рассчитывается как для ТП децентрализованного внутреннего электроснабжения;
для ТП децентрализованного внутреннего электроснабжения;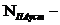 число преобразовательных агрегатов, установленных на тяговой подстанции;
число преобразовательных агрегатов, установленных на тяговой подстанции; ,
, Ом.
Ом.

 А,
А,
 А,
А,
 А.
А. > 1,5
> 1,5 
 > 1,5
> 1,5 
 > 1,5
> 1,5 
 > 1,5
> 1,5 
 3Статистический метод расчёта электрических нагрузок в тяговой сети
3Статистический метод расчёта электрических нагрузок в тяговой сети

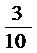



 ,
, .
. Таблица 4- Построение гистограммы
Таблица 4- Построение гистограммы

