
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Эквиваленция (равнозначность)Результатом операции эквиваленции для высказывания А ~ В будет истинна тогда, когда истинны или ложны одновременно оба высказывания. Отличие эквиваленции от конъюнкции состоит в том, что вне зависимости от смысла, равнозначными являются как истинные, так и ложные высказывания. Пример 14. Высказывания А = «2 + 2 = 7» и В = «1 – 8 = 5». Сложное высказывание А º В (А ~ В) истинно, так как оба высказывания ложны.
Импликация Результатом операции импликации для высказывания А ® В будет ложь только тогда, когда первое высказывание (А) истинно, а второе (В) ложно. При этом А – предпосылка, а В – следствие. Пример 15. Высказывания А = «2 + 2 = 4» и В = «1 – 8 = 5». Сложное высказывание А ® В (А Þ В) ложно, так как высказывание А истинно, а В – ложно. Антиконъюнкция Результатом операции антиконъюнкции для высказывания А ½ В будет ложь только тогда, когда оба высказывания истинны. Пример 16. Высказывания А= «Москва – столица России» и В= «Рим – столица Италии». Сложное высказывание А ½ В ложно, так как истинны оба высказывания. Антидизъюнкция Результатом операции антидизъюнкции для высказывания А ¯ В будет истинна только тогда, когда оба высказывания ложны. Пример 17. Высказывания А= «Рим – столица России» и В= «Москва – столица Италии». Сложное высказывание А ¯ В истинно, так как ложны оба высказывания. Основными символами алгебры логики являются:
Переменная, значениями которой являются высказывания, называется пропозициональной переменной. Далее индуктивно вводится понятие формулы, являющееся формализацией понятия «сложного» высказывания. К формуле алгебры логики относят: 
Правила сокращения записей в пропозициональных формулах:
~ ® Ú Ù Ø
Пример 18.
Для преобразований формул в равные формулы важную роль в алгебре логики играют следующие равенства:
Эти равенства позволяют существенно упростить запись формул освобождением от лишних скобок.
Нормальные формы Элементарной конъюнкцией называется конъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причём среди переменных могут быть одинаковые. Элементарной дизъюнкцией называется дизъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причём среди переменных могут быть одинаковые.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 712. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ;
;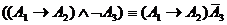 ;
; .
. (закон коммутативности).
(закон коммутативности). (закон ассоциативности).
(закон ассоциативности). (закон поглощения).
(закон поглощения). (закон дистрибутивности).
(закон дистрибутивности).
 (закон противоречия).
(закон противоречия). (закон исключенного третьего);
(закон исключенного третьего); (закон снятия двойного отрицания);
(закон снятия двойного отрицания); (закон склеивания);
(закон склеивания); (закон де Моргана);
(закон де Моргана); (закон свертки).
(закон свертки).