
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Методические указания для выполнения практического задания №1. «Системы счисления»Цель работы: Ознакомиться с системами счислений. Рассмотреть систему представления чисел в памяти ЭВМ. Задание:
Приложение 1. Таблица вариантов заданий
 2. Алгебра логики Логика – одна из древнейших наук. Ее основателем считается древнегреческий мыслитель Аристотель (384 – 322гг. до н. э.), который первым систематизировал формы и правила мышления, обстоятельно исследовал категории понятие и суждение, подробно разработал теорию умозаключений и доказательств, описал ряд логических операций, сформулировал основные законы мышления. Он подвергал анализу человеческое мышление, его формы – понятие, суждение, умозаключение, и рассмотрел со стороны строения, структуры. Логика Аристотеля носит название формальной логики. Это название происходит из принципа: правильность рассуждения определяется только его логической формой или структурой и не зависит от конкретного содержания входящих в него высказываний. Продолжение развития логики связано математической логикой. Основоположником математической логики считается великий математик и философ Готфрид Вильгельм Лейбниц (1646-1716). Он попытался построить первые логические исчисления: арифметические и буквенно-алгебраические. Но Лейбниц высказал только идею, а развил ее окончательно англичанин Джордж Буль (1815-1864). Он вывел для логических построений особую алгебру (алгебру логики). В отличии от обычной логики, в ней символами обозначаются не числа, а высказывания. Алгебра логики (булева алгебра) изучает высказывания, рассматриваемые со стороны их логических значений (истинности или ложности), и логические операции над ними. Создание алгебры логики представляло собой попытку решать традиционные логические задачи алгебраическими методами. С появлением теории множеств (70-е гг. 19 в.), поглотившей часть первоначального предмета алгебры логики, и дальнейшим развитием математической логики (последняя четверть 19 в. – 1-я половина 20 в.) предмет алгебр логики значительно изменился. Основным предметом алгебры логики стали высказывания. Под высказыванием понимается имеющее смысл языковое выражение, относительно которого можно утверждать, что оно либо истинно, либо ложно. Пример 1.
Высказывание считается простым, если никакая его часть не является суждением. Сложное высказывание характеризуется тем, что оно образованно из нескольких высказываний с помощью определенных способов соединения. Пример 2.
Частные высказывания выражают конкретные факты. Общие высказывания характеризуют свойства групп объектов или явлений. Пример 3.
Рассуждение - это цепочка взаимосвязанных высказываний, фактов и общих положений, полученных из других высказываний по определенным правилам вывода. Пример 4.
Умозаключение – прием мышления, посредством которого из исходного знания получается новое знание; из одного или нескольких истинных высказываний, называемых предпосылками, по определенным правилам вывода можно получить заключение. Пример 5. «Все металлы – простые вещества». «Литий – металл». Следовательно «Литий – простое вещество». Любое правило вывода умозаключений состоит из двух высказываний (простых или сложных). Одно из них называется предпосылкой или условием, а второе – следствием, заключением или выводом. Пример 6. «Если треугольник равносторонний, то у него все углы 60 градусов». Высказывание «У него все углы равны 60 градусов» – это заключение, а высказывание «Треугольник равносторонний» – это предпосылка. Существуют умозаключения, осуществляемые по схемам аналогии, индукции и дедукции. Умозаключение по аналогии – это правило полученное из рассмотрения какого-либо объекта, переносимое на менее изученный, сходный по существенным свойствам и качествам объекта. Пример 7. Из высказывания «Солнечная система – это планеты, вращающиеся по орбитам, в центре которых находится Солнце» можно получить умозаключение по аналогии: «Атом – это электроны, вращающиеся по орбитам, в центре которых находится ядро». Индукция – это правило вывода умозаключений при переходе от частных высказываний к общим. Пример 8. Высказывания: «кошки имеют хвост», «собаки имеют хвост», «обезьяны имеют хвост», «кошки, собаки, обезьяна – млекопитающие». Следовательно, «все млекопитающие имеют хвост». Это умозаключение ложно. Индуктивный вывод умозаключений позволяет формулировать различные гипотезы, догадки, но иногда он может приводить и к ошибочным умозаключениям. Дедукция – это правило вывода умозаключений при переходе от общих суждений к частным. Пример 9. «Умные люди не делают ошибки». «Я – умный человек». Следовательно: «Я не делаю ошибок». В математической логике не рассматривается конкретное содержание высказывания, важно только, истинно оно или ложно. Поэтому высказывания можно представить некоторой переменной величиной, значением которой может быть только «0» или «1». Если высказывание истинно, то его значение равно «1», если ложно, то равно «0». Из заданных простых высказываний можно строить более сложные высказывания, используя частицу «не», а также союзы «и», «или», «если..., то...», «тогда и только тогда, когда» и т.п..
Логические операции Истинностные значения новых высказываний определяются при этом только истинностными значениями входящих в них высказываний. Построение из данных высказываний (или из данного высказывания) нового высказывания называется логической операцией. Знаки логических операций называются логическими связками. Логические связки бывают одноместными (унарными), двухместными (бинарные), трехместными (тернарными) и т.д. Пример 10.
Истинность или ложность получаемых таким образом высказываний зависит от истинности и ложности исходных высказываний и соответствующей трактовки связок как операций над высказываниями. В алгебре логики логические операции чаще всего описываются при помощи таблиц истинности. В таблице 1 представлена таблица истинности для операции «отрицание» («инверсия»).
Таблица истинности для операции «отрицания» Таблица 1
В таблице 2 приведены основные бинарные логические операции и связки. Основные бинарные логические операции и связки Таблица 2
Примечание: А1 и А2 являются высказываниями. Связки и частица «не» рассматриваются в алгебре логики как операции над величинами, принимающими значения 0 (ложь/false) и 1 (истина/true), и результатом применения этих операций также являются числа 0 или 1. В таблице 3 представлены все наборы значений переменных А1 и А2 и значения функций на этих наборах. Таблица истинности для основных бинарных логических операций Таблица 3
Инверсия Отрицание высказывания А (т.е. не А) обозначается Пример 11. Высказывание А=<Киев-столица Франции>, тогда сложное высказывание НЕ А означает: не верно, что А, т.е. не верно, что <Киев-столица Франции>.
Результатом операции конъюнкции для высказывания А Ù В будет истинна только тогда, когда истинны одновременно оба высказывания. Пример 12. Высказывания А= «Москва – столица России» и В= «Рим – столица Италии». Сложное высказывание А Ù В (А & В) истинно, так как истинны оба высказывания. Дизъюнкция Результатом операции дизъюнкции для высказывания А Ú В будет истинна тогда, когда истинно хотя бы одно высказывание, входящее в него. Пример 13. Высказывания А = «2 + 3 = 5» и В = «3 + 3 = 5». Сложное высказывание: А Ú В (А + В) истинно, так как истинно высказывание А.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 568. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
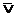 А2
А2
 , или
, или  , или
, или  и часто читается: «отрицание А», «не А» или «А с чертой».
и часто читается: «отрицание А», «не А» или «А с чертой». Конъюнкция
Конъюнкция