Задание 1.  Создание контекстной диаграммы

1. На панели инструментов выберите пиктограмму функции и мышью укажите месторасположение на рабочем пространстве.

2. Дайте данному функциональному блоку имя «Описать деятельность гостиницы».

3. Используя пиктограмму панели инструментов , создайте стрелки на контекстной диаграмме согласно Таблица 1.

Таблица 1. Контекстная диаграмма

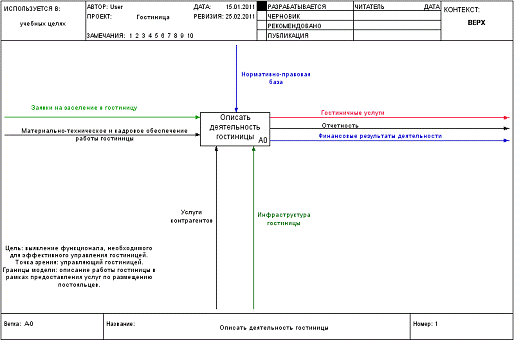
 4. В результате должна получиться контекстная диаграмма, показанная на рисунке

   Контекстная диаграмма предметной области «Гостиница»

Заданеие 2. Создание диаграммы декомпозиции

1. Выберите в палитре инструментов кнопку перехода на нижний уровень , в диалоговом окне «Создание новой диаграммы». Установите количество функциональных блоков 3, укажите тип диаграммы (IDEF0) и нажмите кнопку ОК.

2. Автоматически будет создана диаграмма первого уровня декомпозиции   с перенесенными в нее потоками родительской диаграммы.

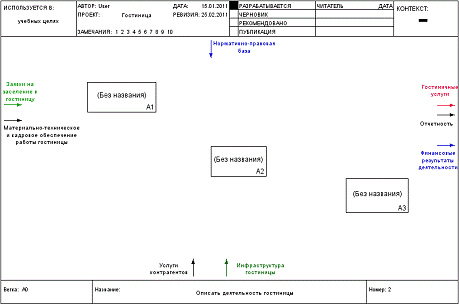
  Рабочее пространство детализирующей диаграммы

  Детализированная диаграмма первого уровня

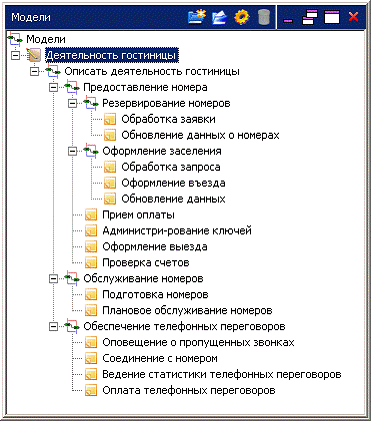
3. Осуществите построение детализирующих диаграмм для функциональных блоков согласно представленной иерархии.

  Иерархия функциональных блоков модели

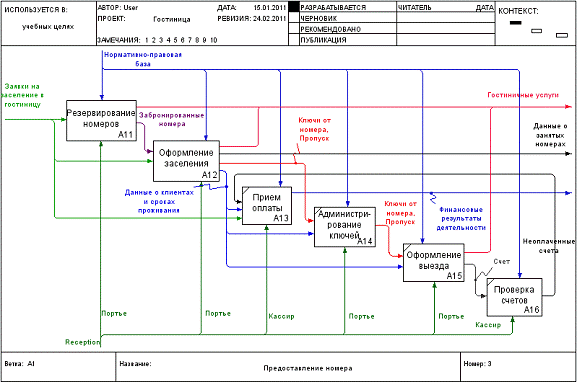
4. В результате должны быть разработаны IDEF0-диаграммы, представленные на рисунках.

  Детализированная диаграмма работы «Предоставление номера»  

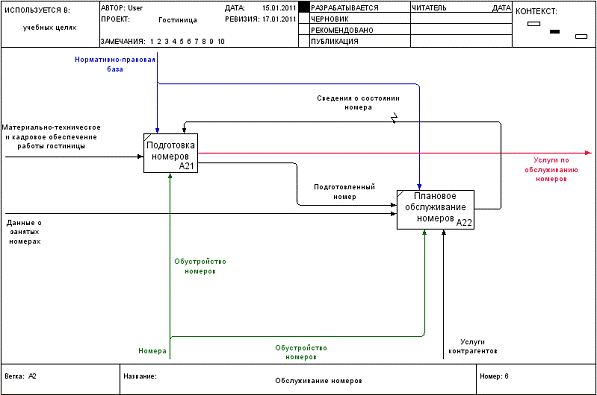
  Детализированная диаграмма работы «Обслуживание номеров»

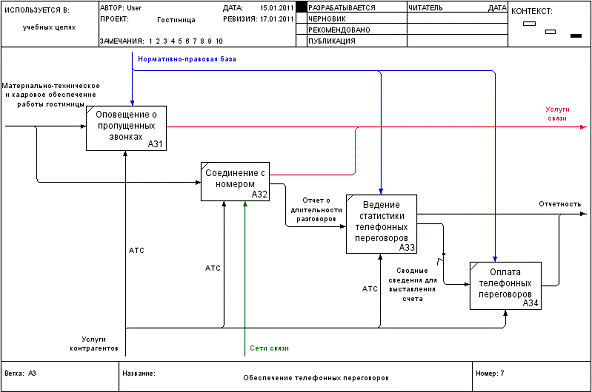
  Детализированная диаграмма работы «Обеспечение телефонных переговоров»

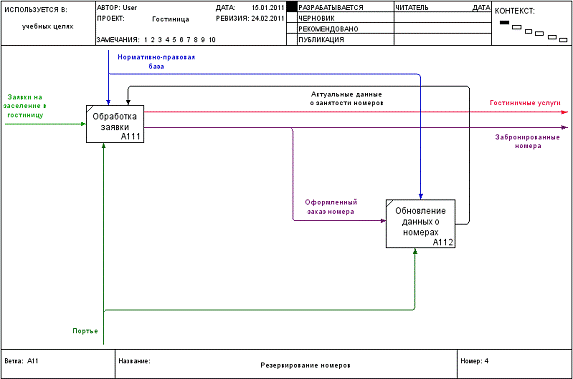
Детализированная диаграмма работы «Резервирование номеров»

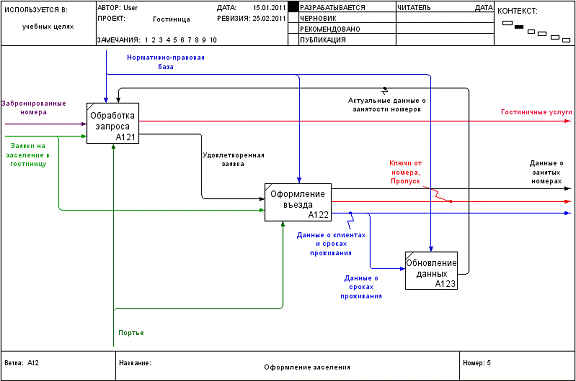
  Детализированная диаграмма работы «Оформление заселения»

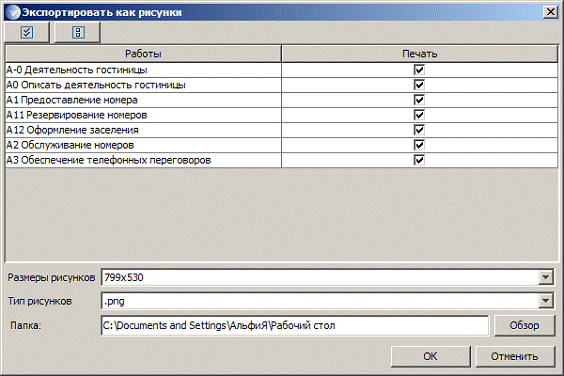
5. В программе Ramus Educational предусмотрена возможность экспорта разработанных диаграмм в виде рисунков формата *.png, *.bmp или *.jpeg.

Для этого в главном меню необходимо выбрать команду «Диаграммы»  «Экспортировать как рисунки». В появившемся окне указывается список экспортируемых рисунков, выбирается их формат и размер, а также путь для сохранения.

  Диалоговое окно экспорта диаграмм

Варианты заданий для самостоятельной работы

Вариант задания выбирается по сумме двух последних цифр зачетной книжки.

1. Автострахование.

2. Агентство по сдаче автомобилей в аренду.

3. Аренда коньков, роликов, велосипедов, лыж.

4. Аэропорт – пассажирское расписание и перевозки.

5. Банковская система вкладов (физических и юридических лиц) .

6. Банковская система кредитования (физических и юридических лиц).

7. Биллинг сотовой компании.

8. Ветеринарная лечебница.

9. Клуб обучения танцам.

10. Магазин косметики.

11. Машиностроительное предприятие: система по разработке и модификации изделий (ведение архива, стандартов и пр.).

12. Нефтеперерабатывающая компания.

13. Парикмахерская.

14. Поставка вин.

15. Приемная комиссия ВУЗа.

16. Производство мебели (прием индивидуальных и типовых заказов и изготовление).

17. Рекламное агентство.

18. Риэлторская компания: аренда; продажа первичного и вторичного жилья.

19. Санаторий.

20. Система управления проектом для IT-компании.

21. Складская логистика.

22. Спа-салон (услуги, обслуживающий персонал и пр.).

23. Страховая компания.

24. Такси.

25. Транспортная логистика.

26. Туристическое агентство (путешествия за рубеж).

27. Туристическое агентство (путешествия по России).

28. Учет оборудования на крупном промышленном предприятии.

29. Филармония.

30. Электронный проездной.

 2 Системы массового обсЛуживания

Задание 1.

  В систему массового обслуживания (СМО) поступает в среднем λ заявок [1/час]. Найти вероятность того, что за время t [мин] в СМО поступит:

а) ровно k заявок;

б) менее k заявок;

в) более k заявок.

Варианты задания:

1.    λ = 60;   t = 5;   k = 4.

2.    λ = 120;  t = 2;   k = 3.

3.    λ = 40;    t = 6;   k = 5.

4.   λ = 30;   t = 4;  k = 4.

5.   λ = 150;  t = 3;  k = 3.

6. λ = 80;   t = 2;   k = 5.

7.    λ = 40;   t = 3;   k = 4.

8.    λ = 100;  t = 2;   k = 3.

9.    λ = 60;   t = 5;   k = 4.

10. λ = 40;   t = 4;   k = 5.

Задание 2.

  Испытывают три элемента, работающих независимо друг от друга. Длительность времени безотказной работы элементов распределена по показательному закону и равна t₁, t₂, t₃ [час]. Найти вероятность того, что в интервале времени [0, t_отк] откажут:

а) только один элемент;

б) не более 2-х элементов;

в) все три элемента.

Варианты задания:

1.    t₁ = 20;    t₂ = 50;      t₃ = 40;    t_отк = 18.

2.  t₁ = 10;    t₂ = 20;      t₃ = 25;    t_отк = 15.

3.    t₁ = 20;    t₂ = 8;        t₃ = 10;    t_отк = 6.

4.    t₁ = 8;      t₂ = 4;        t₃ = 5;    t_отк = 3.

5.   t₁ = 10;   t₂ = 5;        t₃ = 4;      t_отк = 5.

6.  t₁ = 12;   t₂ = 9;        t₃ = 12;    t_отк = 8.

7.  t₁ = 16;    t₂ = 12;      t₃ = 26;    t_отк = 12.

8.  t₁ = 14;  t₂ = 10;      t₃ = 18;    t_отк = 18.

9.  t₁ = 10;  t₂ = 25;      t₃ = 14;    t_отк = 16.

10.  t₁ = 22;   t₂ = 16;      t₃ = 18;    t_отк = 15.

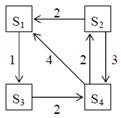
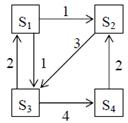
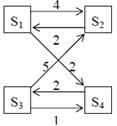
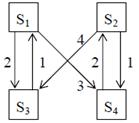
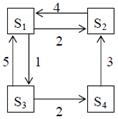
Задание 3.

  Рассматривается система с дискретными состояниями и дискретным временем (цепь Маркова). Задана матрица вероятностей перехода за один шаг. Требуется:

а) построить размеченный граф состояний;

б) найти распределение вероятностей для первых 3-х шагов, если известно, что в начальный момент времени (t₀ = 0) система находилась в j-ом состоянии с вероятностью p_j(0).

Варианты задания:

1
2
3
4
5
6
7
8
9
10

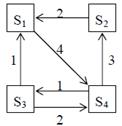
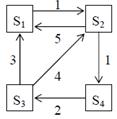
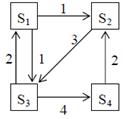
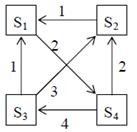
Задание 4.

  Рассматривается система с дискретными состояниями и непрерывным временем. Заданы размеченный граф состояний и интенсивности переходов. Все потоки событий простейшие. Требуется:

а) составить матрицу интенсивностей переходов;

б) составить систему дифференциальных уравнений Колмогорова для вероятностей состояний;

в) найти предельное распределение вероятностей.

Варианты задания:

1		6
2		7
3		8
4		9
5		10

Задание 5.

  Рассматривается n-канальная система массового обслуживания (СМО) с отказами. Поток заявок, поступающих в СМО, простейший с интенсивностью λ [1/час]. Среднее время обслуживания заявки равно t_об [мин]. Время обслуживания распределено по показательному закону. Определить:

а) число каналов, при котором вероятность того, что заявка получит отказ, не больше α;

б) абсолютную пропускную способность СМО;

в) среднее число каналов, занятых обслуживанием заявок;

г) среднее время пребывания заявки в СМО;

д) среднее время простоя одного (произвольно взятого) канала.

Варианты задания:

 1.  λ = 12;    t_об = 12;     α = 0,07.   6.λ = 6;    t_об = 15;   α = 0,02.

2.  λ = 13;    t_об = 12;     α = 0,08.        7.λ = 7;      t_об = 15;   α = 0,03.

3.   λ = 19;    t_об = 6;       α = 0,04.        8.λ = 11;    t_об = 12;   α = 0,05.

4.   λ = 9;      t_об = 15;     α = 0,06.        9.λ = 5;      t_об = 30;   α = 0,07.

5.   λ = 9;      t_об = 12;     α = 0,03.       10.λ = 11;   t_об = 15;   α = 0,09.

Задание 6.

  Рассматривается n-канальная система массового обслуживания (СМО) с ожиданием. Поток заявок, поступающих в СМО, простейший с интенсивностью λ [1/час]. Среднее время обслуживания заявки равно t_об [мин]. Время обслуживания распределено по показательному закону. Определить:

а) существует ли стационарный режим работы СМО;

б) среднее число заявок, находящихся в СМО;

в) среднее время пребывания заявки в СМО;

г) вероятность того, что все каналы заняты;

д) среднее время простоя одного (произвольно взятого) канала.

Задание 7.

  Рассматривается n-канальная система массового обслуживания (СМО) с ожиданием и ограничением на длину очереди. Число мест в очереди равно m. Поток заявок, поступающих в СМО, простейший с интенсивностью λ [1/час]. Среднее время обслуживания заявки равно t_об [мин]. Время обслуживания распределено по показательному закону.

Варианты задания:

 1.n = 4; m = 3; λ = 6; t_об = 40. Определить:

а) среднее число заявок, находящихся под обслуживанием;

б) вероятность того, что заявка сразу же будет принята к обслуживанию;

в) вероятность того, что в СМО будет не более 2-х заявок.

 2.n = 3; m = 4; λ = 8; t_об = 15. Определить:

а) вероятность того, что заявка получит отказ в обслуживании;

б) среднее число каналов, не занятых обслуживанием;

в) среднее время пребывания заявки в СМО;

3.n = 4; m = 2; λ = 4; t_об = 60. Определить:

а) среднее число заявок в СМО;

б) среднее время пребывания заявки в очереди;

в) вероятность того, что будет простаивать не более одного канала.

4. n = 3; m = 3; λ = 6; t_об = 20. Определить:

а) относительную пропускную способность СМО;

б) среднее число каналов, занятых обслуживанием заявок;

в) среднее время пребывания заявки в СМО.

5.n = 3; m = 4; λ = 9; t_об = 20. Определить:

а) абсолютную пропускную способность СМО;

б) среднее число заявок в очереди;

в) вероятность того, что не более 2-х каналов будут заняты обслуживанием заявок.

6.n = 3; m= 3; λ = 5; t_об = 30. Определить:

а) вероятность того, что заявка получит отказ в обслуживании;

б) среднее число заявок, находящихся под обслуживанием;

в) вероятность того, что менее 2-х заявок будут находиться в очереди на обслуживание.

 7.n = 2; m = 4; λ = 6; t_об = 15. Определить:

а) среднее число свободных каналов;

б) вероятность того, что заявка будет принята в СМО;

в) вероятность того, что заявка, поступившая в СМО, встанет в очередь на

обслуживание.

 8. n = 4; m = 3; λ = 5; t_об = 30. Определить:

а) среднее число заявок, находящихся в СМО;

б) вероятность того, что заявка сразу же будет принята к обслуживанию;

в) вероятность того, что не более 2-х каналов будет занято обслуживанием заявок.

 9.n = 4; m= 3; λ = 9; t_об = 20 . Определить:

а) абсолютную пропускную способность;

б) среднее время пребывания заявки в СМО;

в) среднее число заявок в очереди.

10.n = 3; m= 4; λ = 6; t_об = 15 . Определить:

а) относительную пропускную способность СМО;

б) среднее время ожидания заявки в очереди;

в) среднее число занятых каналов.

Задание 8.

  Рассматривается n-канальная система массового обслуживания (СМО) без ограничения на длину очереди, но с ограничением на время ожидания. Заявка ожидает обслуживания в среднем t_ож [мин], а затем покидает СМО. Поток заявок, поступающих в СМО, простейший с интенсивностью λ [1/час], среднее время обслуживания заявки равно t_об [мин].

Варианты задания:

 1.n = 4; λ = 8; t_об = 15; t_ож = 5. Определить:

а) абсолютную пропускную способность СМО;

б) среднее число заявок в очереди;

в) вероятность того, что в очереди будут находиться не более 2-х заявок.

2.n = 3; λ = 6; t_об = 30; t_ож = 15. Определить:

а) среднее число заявок, находящихся под обслуживанием;

б) вероятность того, что заявка уйдет из очереди не обслуженной;

в) вероятность того, что менее 3-х заявок будут находиться в очереди на обслуживание.

3.n = 4; λ = 9; t_об = 20; t_ож = 10. Определить:

а) вероятность того, что заявка будет обслужена;

б) среднее время пребывания заявки в СМО;

в) среднее число свободных каналов.

4.n = 3; λ = 10; t_об = 15; t_ож = 12. Определить:

а) среднее число заявок, находящихся в СМО;

б) вероятность того, что заявка сразу же будет принята к обслуживанию;

в) среднее время простоя канала.

5.n = 3; λ = 8; t_об = 30; t_ож = 10. Определить:

а) среднее число заявок в очереди;

б) абсолютную пропускную способность СМО;

в) среднее время пребывания заявки в СМО.

6.n = 4; λ = 10; t_об = 15; t_ож = 6. Определить:

а) среднее число занятых каналов;

б) относительную пропускную способность СМО;

в) среднее время ожидания заявки в очереди.

7.n = 3; λ = 6; t_об = 20; t_ож = 12. Определить:

а) вероятность  того, что заявка сразу же будет принята к обслуживанию;

б) среднее число заявок, находящихся под обслуживанием;

в) вероятность того, что в СМО будет не более 4-х заявок.

8.n = 4; λ = 12; t_об = 12; t_ож = 6. Определить:

а) вероятность того, что заявка уйдет из СМО не обслуженной;

б) среднее время пребывания заявки в СМО;

в) среднее число каналов, не занятых обслуживанием.

9.n = 3; λ = 15; t_об = 12; t_ож = 3. Определить:

 а) среднее число заявок в СМО;

б) среднее время простоя канала;

в) вероятность того, что будет простаивать не более одного канала.

10.n = 4; λ = 10; t_об = 12; t_ож = 3. Определить:

а) относительную пропускную способность СМО;

б) среднее время пребывания заявки в СМО;

в) среднее число каналов, занятых обслуживанием заявок.

Задание 9.

  Рассматривается n-канальная система массового обслуживания (СМО) замкнутого типа с m источниками заявок. Поток заявок, поступающих в СМО, простейший с интенсивностью λ [1/час], среднее время обслуживания заявки равно t_об [мин].

Варианты задания:

 1.n = 2; m = 7; λ = 3; t_об = 15. Определить:

а) среднее число заявок, находящихся под обслуживанием;

б) среднее время ожидания заявки в очереди;

в) вероятность того, что не менее 4-х источников будут находиться в активном

состоянии.

 2.n = 3; m= 8; λ= 2; t_об = 20. Определить:

а) среднее число заявок в очереди;

б) среднее время простоя источника;

в) вероятность того, что не более 5-ти источников будут находиться в пассивном

состоянии.

3.n = 2; m = 8; λ = 1; t_об = 30. Определить:

а) среднее число заявок в СМО;

б) вероятность того, что поступившая заявка сразу же будет принята к обслуживанию;

в) вероятность того, что не менее 4-х заявок будут ожидать в очереди на обслуживание.

 4.n = 3; m = 7; λ= 2; t_об = 15. Определить:

а) среднее число простаивающих каналов;

б) вероятность того, что поступившая заявка встанет в очередь для ожидания начала

обслуживания;

в) вероятность того, что будет простаивать не более одного канала.

 5.n = 4; m = 8; λ = 3; t_об = 12. Определить:

а) среднее число занятых каналов;

б) среднее время простоя канала;

в) вероятность того, что более 2-х источников будут находиться в активном состоянии.

 6.n = 3; m = 7; λ= 4; t_об = 10. Определить:

а) вероятность того, что произвольный источник находится в активном состоянии

(коэффициент готовности);

б) среднее время пребывания заявки в СМО;

в) вероятность того, что в очереди на обслуживание будет более 2-х заявок.

7.n = 3; m = 8; λ = 3; t_об = 10. Определить:

а) среднее число заявок в очереди;

б) вероятность того, что поступившая заявка немедленно будет принята к

обслуживанию;

в) вероятность того, что заняты все каналы.

 8.n = 2; m = 8; λ = 2; t_об = 12. Определить:

а) среднее число источников, находящихся в пассивном состоянии;

б) вероятность того, что поступившая заявка встанет в очередь для ожидания начала

обслуживания;

в) вероятность того, что в очереди на обслуживание окажется не более 3-х заявок.

 9.n = 4; m = 7; λ = 6; t_об = 7,5. Определить:

а) вероятность того, что произвольный источник находится в активном состоянии

(коэффициент готовности);

б) среднее число простаивающих каналов;

в) среднее время ожидания заявки в очереди.

10.n = 3; m= 8; λ= 9; t_об = 4. Определить:

а) среднее число занятых каналов;

б) среднее время простоя канала;

в) вероятность того, что в СМО будет менее 6-ти заявок.

Формулы для вычислений

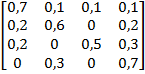
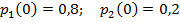
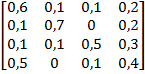
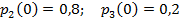
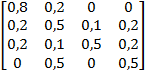
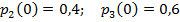
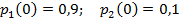
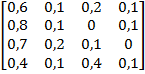
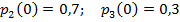
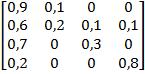
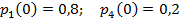
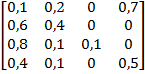
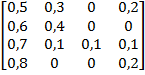
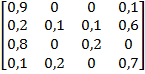
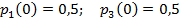
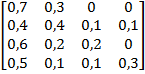
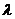 -интенсивность потока заявок

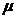 -интенсивность потока обслуживания

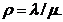- интенсивность нагрузки

T -интервал времени между двумя заявками (случайная величина)

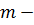 длина очереди (число мест)

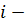 количество заявок, поступающих в СМО