Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
СЕТЕВЫЕ МЕТОДЫ МОДЕЛИРОВАНИЯ
Алгоритмы решения задач на сетях
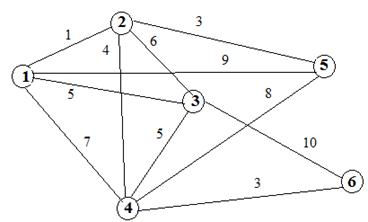
Алгоритм нахождения минимального остовного дерева Обозначим черезх N множество вершин сети N={1,2,...n} Ck - множество вершин включенных в остовное дерево на k- ом шаге. ШАГ 1. Выбираем любую вершину графа i из множества ШАГ 2. В множестве ШАГ 3. В множестве Процесс продолжается до включения всех вершин в остовное дерево. Пример:
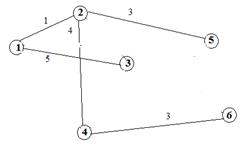
Начнем с вершины1. Ребро 1-2 самое короткое, поэтому включаем в остовное дерево вершину 2. Анализируем длины всех ребер соединяемых (инцидентных_ вершинам 1 и 2. Выбираем вершину 5. Следующей вершиой выбиаем 4. Далее 6 вершиа. Следующая и последняя вершина 3. Подсчитаем общее растояние: 1+3+4+3+5=16 Дерево будет иметь вид:
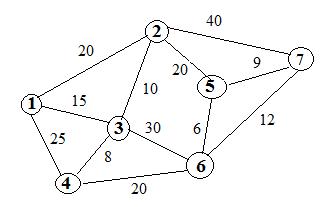
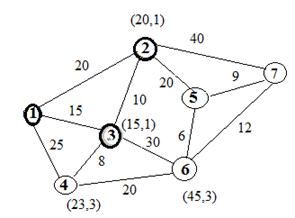
Алгоритм нахождения кратчайшего пути Алгоритм Дейкстры Рассмотрим работу алгоритма на примере. Найдем кратчайший путь между вешинами 1-7.
Шаг. Выделяем узел 1. Помечем все узлы связые с 1 метками.
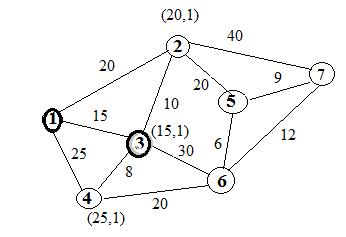
Эти метки (вреенные) указывают на номер узла , связанного с данным узлом. На этом шаге это первый узел. Первая цифра метки указывает расстояние до первого узла. Ребро, связывающее узел 3 с узлом 1 самое короткое. Поэтому 3 узел помечаем постоянной меткой. Шаг. Отбираем все узлы, которые соединяются с 3 одним ребром и не имеют постоянных меток. Это узлы 2, 4,6. Срниаем маршрты 1-2 и 1-3-2 замечаем, что длина перого 20 меньше второго 25. Следоателно метка узла 2 не меняется (мы не идем от 3 к 2).  Сравниваем маршуты 1-4 и 1-3-4. Последни короче. Поэтому временная метка узла 4 менется на (23,3). Аналогичные рассуждения для узла 6. Его метка будет (15+30,3)=(45,3) Ребро соединяющее 2 и 1 самое короткое. Любой маршрут от 1 к узлу 2 будет длиннее. Поэтому узлу 2 приписывается постоянная метка.
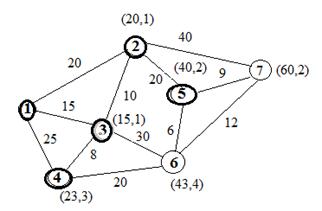
Шаг. Отбраем все узлы, которые соединены с узлом 2 одним ребром и не имеют постоянных меток. Это узел 6. Узел 5 получает метку (40,2) Узел 7 получает метку (60,2) Путь 1-3-4 кратчайший к узлу 4. Поэтому делаем ему постоянную метку.
Шаг. Отбраем все узлы, которые соединены с узлом 4 одним ребром и не имеют постоянных меток. Это узлы 5 и 7. Сравниваем маршруты 1-3-6 и 1-3-4-6 Получаем 45 и 43. Второй короче. Меняем узлу 6 метку на (43,4). Маршрут 1-2-5 кратчайший к узлу 5. Поэтому делаем узлу 5 постоянную метку (40,2).
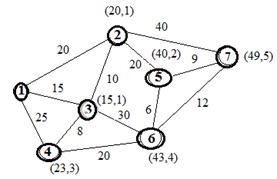
Следующие шаги приводят к постоянной метке узла 6 (43,4) и (49,5) для узла 7. Таким образом кратчайший путь 49.
Кратчаий путь отконца 7-5-2-1 Замечание: На каждом шаге временная метка одного из узлов меняется на постоянную по следующему правилу: рассматриваются все узлы с временными метками и выбирается тот из них, длина маршрута которого до1 является минимальной. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 369. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

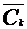 - оставшиеся вершины.
- оставшиеся вершины.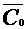
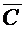 выбираем вершину j , которая соединена самой короткой дугой с выбранной начальной вершиной.
выбираем вершину j , которая соединена самой короткой дугой с выбранной начальной вершиной.