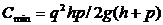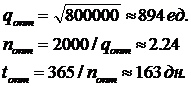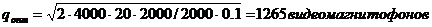Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
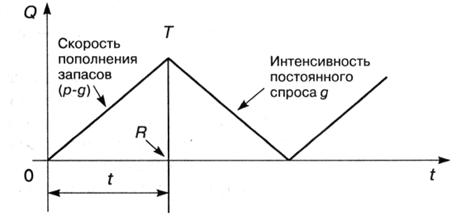
Модель производственных поставокВ основной рассмотренной выше модели предполагалось, что поступление товаров на склад происходит мгновенно, например в течение одного дня. Рассмотрим случай, когда готовые товары поступают на склад непосредственно с производственной линии. Будем считать, что поступление товаров происходит непрерывно. Модель задачи в этом случае называют моделью производственных поставок. Обозначим через р скорость поступающего на склад товара. Эта величина равна количеству товаров, выпускаемых производственной линией за год. Остальные обозначения и предположения те же, что и для основной модели управления запасами. Определим оптимальный размер партии, минимизирующий общие затраты. График изменения модели производственных поставок представлен на рисунке 3.4.
Рисунок 3.4- График изменения модели производственных поставок Общие издержки в течение года, как и для основной модели, составляют Для получения среднего уровня запасов следует учесть, что RT=(p-g)t – максимальный уровень запасов; q=pt – количество товаров в одной производственной поставке. Тогда средний уровень запасов составляет половину максимального и равен В итоге Решая уравнение
Модель запасов, включающая штрафы
Рассмотрим основную модель, допускающую возможность существования периодов дефицита, который покрывается при последующих поставках, и штрафов за несвоевременную поставку.  Пусть предприятие должно поставить q ед. товара в течение каждого промежутка времени L, за единицу времени поставляется g ед. товара (q = Lg). Предположим, что в начале каждого периода L предприятие делает запас, равный k. Это означает, что в течение периода будет наблюдаться дефицит товара и некоторое время поставки не будут осуществляться. Невыполненные заявки будут накапливаться до максимальной величины q- k и будут удовлетворены, как только поступит следующая партия товаров в количестве q. За то, что товары доставляются предприятием позже необходимого срока, на предприятие налагается штраф, который зависит от того, насколько была задержана поставка. Такая модель целесообразна, поскольку иногда выгоднее заплатить штраф, чем расходовать дополнительные средства на хранение запасов, превышающих величину k. Задача управления запасами состоит в том, чтобы выбрать такое значение k, которое ведет к минимизации всех затрат, включая затраты на хранение и штрафы. График изменения запасов представлен на рисунке 3.5.
Рисунок 3.5 – Управление запасами со штрафами Для определения оптимального значения k обозначим: h- издержки хранения единицы товара за единицу времени; p – затраты на штраф в расчете на единицу товара за один день отсрочки. Найдем издержки одного цикла: С=С1+С2, Где С1- общие издержки содержания запасов; С2- общие затраты на штраф. Так как товары находятся на складе в течение периода ОА, средний уровень запасов за этот период равен k/2 . Если продолжительность периода равна k/g, то Так как штраф выплачивается в течение периода АВ= (q-k)/g, общее число «товаро-дней», на которые налагается штраф, равно площади треугольника АВС. Площадь составляет: Откуда Решив уравнение Тогда минимальные расходы будут равны:
Примеры решения задач Пример 1. Интенсивность равномерного спроса составляет 200 телевизоров в год. Организационные издержки для одной партии составляют 20 тыс. . Цена единицы товара составляет 1 тыс. , а издержки содержания телевизоров составляют 0.1 тыс. за один телевизор в год. Найти оптимальный размер партии, число поставок и продолжительность цикла. Решение: По условию задачи g=2000, b=20, s=1, h=0.1 Общие издержки в течение года:
С=С1+С2+С3=40000/q + 2000 + q/20 dC/dq =-40000/q =1/20
Ответ: Оптимальный размер партии составляет 894 телевизора, число поставок – 2.24, продолжительность цикла 163 дня.
Пример 2. Интенсивность равномерного спроса выпускаемых фирмой видеомагнитофонов составляет 2000 шт. в год. Организационные издержки равны 20 тыс. . Цена видеомагнитофона составляет 1 тыс., издержки хранения равны 0,1 тыс. в расчете на один видеомагнитофон в год. Запасы на складе пополняются со скоростью 4000 видеомагнитофонов в год. Производственная линия начинает действовать, как только уровень запасов на складе становится равным нулю, и продолжает работу до тех пор, пока не будет произведено q видеомагнитофонов. Найти размер партии, который минимизирует все затраты. Определить число поставок в течение года, время, в течение которого продолжается поставка, продолжительность цикла, максимальный уровень запасов и средний уровень запасов при условии, что размер поставки оптимален.
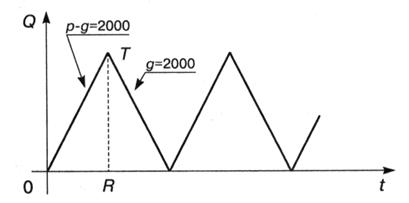
Решение: Данная модель задачи является моделью производственных поставок со следующими параметрами: g = 2000, b = 20, h = 0,1, s = 1, р = 4000. График изменения запасов имеет следующий вид:
Число партий в течение года n=g/q =2000/q Продолжительность поставки: T=q/p = q/4000 Продолжительность цикла: L=1/n=q/g=q/2000 Максимальный уровень запасов: RT = (p-g)t = 2000q/4000 =q/2 Средний уровень запасов: RT/2 = q/4 Уровень издержек: С=С1+С2+С3= bn +sg + qh/4 Ответ: За каждую поставку необходимо доставлять на склад 1265 видеомагнитофонов, оптимальное число поставок 1.6, продолжительность поставки – 115 дней, продолжительность цикла – 230 дней. Варианты заданий Вариант 1. В течение 10 дней наблюдалось следующее изменение запасов: · Первоначальный запас равен нулю, в следующие двое суток товары поступали на склад непрерывно и равномерно по 500 шт. в день, расходования запасов не происходило. · В следующие четыре дня спрос на имеющиеся в запасе товары был непрерывным и равномерным и равнялся 250 шт. в день, пополнения запасов не происходило; · В следующие четыре дня потребность в товарах изменилась до 200 шт. в день, с целью удовлетворения спроса и пополнения запасов ежедневно на склад доставлялось 300 шт. (поставки на склад и со склада происходили равномерно и непрерывно). Постройте график изменения запасов для 10-дневного периода, определите величину запасов на складе к концу периода. Вычислите средний уровень запасов для всего периода.
Вариант 2. Фирме по строительству судов требуется 20000 заклепок в год, расходуемых с постоянной интенсивностью. Организационные издержки составляют 0,5 тыс. р. за партию, цена одной заклепки — 10 р. Издержки на хранение одной заклепки оценены в 12,5% ее стоимости. Найти оптимальный размер партии поставки, оптимальную продолжительность цикла и оптимальное число поставок за год.
Вариант 3. Известно, что издержки выполнения заказа — 2 ден. ед., количество товара, реализованного за год, — 10000 шт., закупочная цена единицы товара — 5 ден. ед., издержки хранения — 20% от закупочной цены. Определить наиболее оптимальный размер заказа.
Вариант 4. Система управления запасами некоторого товара подчиняется основной модели. Каждый год с постоянной интенсивностью спрос составляет 15 000 ед. товара, издержки на организацию поставки составляют 10 р. на партию, цена единицы товара — 30 р., а издержки на ее хранение — 7,5 р. в год. Найти оптимальный размер партии и число поставок.
Вариант 5. Интенсивность равномерного спроса — 20000 ед. товара в год. Организационные издержки для одной партии —20 тыс. р., цена единицы товара — 1 тыс. р., издержки содержания запаса — 200 р. за единицу товара в год. Найти оптимальный размер партии, предполагая, что система описывается основной моделью.
Вариант 6. Предприниматель имеет стабильный месячный спрос на товар в количестве 500 ед. Товар он покупает у поставщика по цене 5 ден. ед. за штуку, причем издержки на оформление поставки и другие подготовительные операции составляют в каждом случае 10 ден. ед. Как часто предприниматель должен пополнять свой запас товаров, если затраты на хранение равны 20% цены товара?
Вариант 7. Фирма вместо оптимального значения партии товара q в основной модели поставок заказала на 50% больше. На сколько изменятся общие издержки на содержание запасов и организацию поставок по сравнению с оптимальным вариантом поставок товара?
Вариант 8. Известно, что издержки выполнения заказа равны 10 ден. ед., годовой спрос на товар -1470 т, оптимальный размер партии поставки -35 т. Определить годовые затраты на выполнение заказа.
Вариант 9. Пользующийся спросом товар продается со средней скоростью 45 ед. в день, а производится со скоростью 450 ед. в день. Затраты на организацию и доставку товара составляют 5 тыс. р. за партию, издержки хранения запасов равны 20% стоимости товара. Стоимость товара складывается следующим образом: заработная плата обслуживающего персонала составляет 0,4, расходы на материалы — 0,5, накладные расходы — 0,6 (р. за единицу товара, для каждой единицы товара эти значения суммируются). Найти оптимальный размер партии и минимальные общие затраты, связанные с образованием запаса. В году — 300 рабочих дней.
Вариант 10. Интенсивность спроса в модели производственных поставок составляет четверть скорости производства, которая равна 20000 ед. товара в год. Организационные издержки для одной партии равны 150 р., а издержки хранения единицы товара в течение года — 5р. Определить оптимальный размер партии.
Вариант 11. Система управления запасами описывается моделью производственных запасов. Спрос товара — 1500 шт. в год, цена — 200 р., издержки хранения товара в течение года — 20 р., организационные издержки — 1000 р. В течение года может быть произведено 4500 шт. товара при полной загрузке производственной линии. В году — 300 рабочих дней. Нарисуйте график изменения запасов, вычислите оптимальный размер партии, продолжительность поставки, продолжительность цикла и средний уровень запасов.
Вариант 12. Фирма, выступающая в качестве посредника, обязуется поставлять заводу по производству двигателей 5 коленчатых валов в день. Руководство фирмы решает доставлять коленчатые валы на свой склад партиями, причем в каждой содержится 150 шт. и они рассчитаны на 30-дневный срок. За один просроченный день в поставке коленчатого вала заводу фирма выплачивает штраф 200 р. Издержки хранения одного коленчатого вала были оценены в 250 р. в день, организационными затратами можно пренебречь. Найти оптимальный уровень запасов и продолжительность соответствующего ему периода дефицита. Вычислите уменьшение затрат при оптимальной политике управления запасами по сравнению с политикой, когда в начале каждого периода на склад поступает 150 коленчатых валов.
Вариант 13. Магазин «Лада» закупает духи «Ландыш» на одной из парфюмерных фабрик. Годовой спрос на этот продукт составляет 600 шт. Издержки заказа равны 850 руб., издержки хранения — 500 руб. за одну упаковку (20 шт.) в год. Магазин заключил договор на поставку с фиксированным интервалом времени. Количество рабочих дней в году — 300. Время поставки товара 6 дней. Стоимость одного флакона 135 руб. Требуется определить оптимальное число заказов в течение года, точку восстановления запаса, минимальные совокупные издержки.
Вариант 14. При строительстве моста длиной 500 м через крупную водную преграду расходуется большое количество специальных тяжей из высокопрочной стали (130 кг/пог.м), изготавливаемых на одном из местных предприятий и систематически доставляемых на приобъектный склад партиями по q тяжей. Среднесуточный расход тяжей на строительстве постоянен. Нехватка тяжей недопустима, так как из-за этого будут нарушены сроки строительства. Срок строительства моста равен 50 суткам. Завод, изготавливающий тяжи, доставляет их своим транспортом, причем грузоподъемность автомобиля, выделенного для этих целей, используется, как правило, не полностью. Поэтому стоимость доставки партии из q тяжей является постоянной s = 6 у.е., не зависящей от q. Суточные затраты на хранение тяжей, исчисленные для одной детали, равны h = 1,33 у.е. (на 1 т тяжей в течение суток). Эти затраты обусловлены необходимостью строительства склада и его эксплуатации в течение времени строительства моста. Требуется найти оптимальное число тяжей qопт в партии, при котором суммарные затраты на создание и хранение запаса были бы минимальными. Необходимо также найти период пополнения запаса.
Вариант 15. Хлебозаводу для нормальной работы требуется 200 тыс.т муки в год. Затраты на оформление одного заказа составляют 400 рублей. Стоимость транспортировки составляет 1200 руб за 1 т. Стоимость хранения муки на арендуемом складе – 600 руб. в год за 1 т. Определить совокупные затраты при объемах заказа 5, 10, 15, 20, 30, 50 и 100 тыс.т. Выбрать оптимальный размер заказа, исходя из минимума совокупных затрат. Построить графики зависимости годовой стоимости хранения запасов, оформления заказов и совокупных затрат от объема заказа. Рассчитать оптимальный размер заказа.
Вариант 16. Заводу, производящему лакокрасочные материалы для производства белил требуется в год 200 м3 двуокиси титана, который закупается у зарубежного поставщика. Затраты на оформление таможенных документов составляют 5000 рублей за один заказ. Прочие затраты, связанные с оформлением заказа(командировка сотрудника, проверка качества сырья, телефонные переговоры), равны 20000 руб. товар перевозится в специальных грузовиках емкостью 10 м3, стоимость рейса одной машины – 3000 руб., при этом предприятие получает сразу весь заказ. Издержки на хранение двуокиси титана на складе составляют 2500 руб в год за 1 м3. Определить совокупные затраты при объеме заказа 10, 20, 30, 40, 60, 80, 100 и 200 м3. Выбрать оптимальный размер заказа, исходя из минимума совокупных затрат. Построить графики зависимости годовой стоимости хранения запасов, оформления заказов и совокупных затрат от объема заказа. Рассчитать оптимальный размер заказа.
Вариант 17. Оптово-розничная торговая база реализует сахарный песок. Спрос на данный товар составляет 16 т в месяц. Затраты на оффшор – 1 машина, вместимостью 40 мешков по 50 кг каждый, стоимость перевозки равна 1200 руб. за машину. Стоимость хранения на арендуемом складе – 50 руб. в месяц за 1 мешок. Определить совокупные затраты при объеме заказа 40, 80, 120, 160, 200 и 320 мешков. Выбрать оптимальный размер заказа, исходя из минимума совокупных затрат. Построить графики зависимости годовой стоимости хранения запасов, оформления заказов и совокупных затрат от объема заказа. Рассчитать оптимальный размер заказа. Вариант 18. Бензозаправочной станции для нормальной работы требуется 420 т бензина в месяц. Затраты на оформление одного заказа составляют 1200 рублей. Минимальный размер заказа – 1 бензовоз вместимостью 5 т, стоимость перевозки равна 5000 руб. за машину. Издержки по хранению бензина в резервуарах равны 600 руб. в месяц за 1 т. Определить совокупные затраты при объеме заказа 5, 10, 20, 40, 80 и 160 т. Выбрать оптимальный размер заказа, исходя из минимума совокупных затрат. Построить графики зависимости годовой стоимости хранения запасов, оформления заказов и совокупных затрат от объема заказа. Рассчитать оптимальный размер заказа.
Вариант 19. Для керамического завода расход глиносодержащих руд составляет 250 т в год. Затраты на оформление одного заказа равны 2000 руб. Минимальный размер заказа – 1 машина грузоподъемностью 5 т, стоимость перевозки – 3000 руб. за машину. Издержки по хранению глиносодержащих руд на собственном складе предприятия – 1200 руб. в год за 1 т. Определить совокупные затраты при объеме заказа 5, 10, 20, 30, 40, 50 и 100 т. Выбрать оптимальный размер заказа, исходя из минимума совокупных затрат. Построить графики зависимости годовой стоимости хранения запасов, оформления заказов и совокупных затрат от объема заказа. Рассчитать оптимальный размер заказа.
Вариант 20. Деревообрабатывающему комбинату для нормальной работы требуется 1200 м3 древесины в год. Затраты на оформление одного заказа составляют 500 руб. Минимальный размер заказа – 1 машина вместимостью 20 м3, стоимость перевозки равна 750 руб. за машину. Стоимость хранения товара на арендуемом складе – 300 руб. в год за 1 м3. Определить совокупные затраты при объеме заказа 20, 40, 60, 80, 160, 300 и 600 м3. Выбрать оптимальный размер заказа, исходя из минимума совокупных затрат. Построить графики зависимости годовой стоимости хранения запасов, оформления заказов и совокупных затрат от объема заказа. Рассчитать оптимальный размер заказа.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 593. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
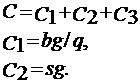
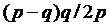
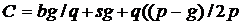 .
.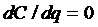 , найдем оптимальный размер партии модели производственных поставок:
, найдем оптимальный размер партии модели производственных поставок: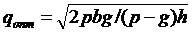 (3.4)
(3.4)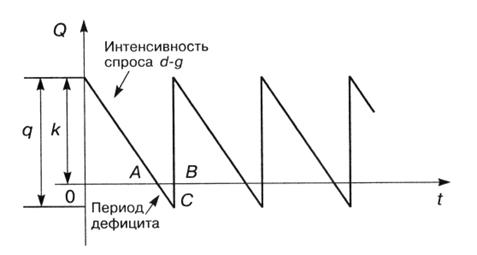
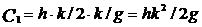
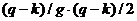
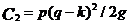 . Окончательно
. Окончательно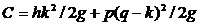 (3.5)
(3.5)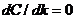 , получим оптимальное значение:
, получим оптимальное значение: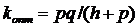 (3.6)
(3.6)