Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Прямая геодезическая задачаВ геодезии часто встречается задача, состоящая в том, что по прямоугольным координатам одной точки находят прямоугольные координаты другой точки, если известны расстояния между этими точками и дирекционный угол линии, их соединяющей.
Рисунок 5.2 По этим данным надо найти прямоугольные координаты хВ и уВ точки В. Из чертежа (рисунок 5.2) мы имеем: хВ = хА +∆ х уВ = уВ +∆ у Следовательно, чтобы найти координаты хВ и уВ , нужно к известным координатам хА и уА прибавить приращение ∆ х и ∆ у Приращением называют разности ∆ х и ∆ у координат последующей и предыдущей точек. Из прямоугольного треугольника (рисунок 5.2) АаВ имеем: ∆ х = s ∙ cos αАВ ∆ у = s ∙ sin αАВ Так как линия может быть направлена под любым (0˚-360˚) углом α, то в расчете угол α заменяют румбом r, поэтому ∆ х = s ∙ cos rАВ ∆ у = s ∙ sin rАВ В зависимости от направления линии АВ меняются знаки координат точек А и В, следовательно приращения координат тоже могут иметь разные знаки. Таблица 5.1 – Зависимость знаков приращений от направления линий
Поэтому формулы для определения прямоугольных координат последующей точки можно записать:
Обратная геодезическая задача Обратная геодезическая задача состоит в том, что по данным прямоугольным координатам начала и конца отрезка прямой определяют дирекционный угол и длину этого отрезка.  Пусть даны координаты точек А и В (рисунок 5.2). необходимо определить длину отрезка АВ – s и величину дирекционного угла αАВ этого отрезка. Из прямоугольного треугольника АаВ имеем: tg αАВ = Принимаем: Ва= ∆ у = уВ – уА Аа = ∆ х = хВ – хА Получим: tg αАВ = Значение длины отрезка АВ может быть вычислено из прямоугольного треугольника АаВ по теореме Пифагора s = При решении обратной задачи для вычисления дирекционного угла пользуются формулой
Примеры решения задач Пример 1.Пусть даны хА = 50,0м, уА = 80,0м, s = 100м, αАВ = 120˚30'. Необходимо вычислить координаты точки В: хВ и уВ. Решение. Вычисления выполняют по следующей схеме. Так как дирекционный угол αАВ больше 90˚, а именно 90˚-180˚, то данный отрезок находится во второй координационной четверти. В расчетах угол αАВ заменяем на румб r. Для второй четверти румб будет равен rAB = 180˚- αАВ = 180˚-120˚30' = 59˚30':ЮВ rAB = 59˚30':ЮВ Так как отрезок АВ находится во второй четверти, знаки приращений будут ∆х (-); ∆у(+), поэтому формулы для вычисления координат точки В хВ и уВ.: хВ = хА - ∆х = хА – s ∙ cos rAB yВ = yА + ∆y = yА – s ∙ sin rAB хВ = 50 – 100 ∙ cos 59˚30' = 50 – 100 ∙ 0,507538 = - 0,754 yВ = yА + ∆y = yА – s ∙ sin 59˚30' = 80 + 100 ∙ 0,861629 = 166,163 Правильность решения задачи можно подтвердить чертежом, выполнив его в масштабе.
Пример 2.Пусть даны прямоугольные координаты точек А и В. Необходимо найти дирекционный угол αАВ и длину линии АВ – s. хА = 20,0м, уА = 30,0м хВ = - 40,0м, уВ = - 60,0м Решение. Приращение координат вычислим по формуле: ∆ у = уВ – уА = - 60 - 30 = -90,0 ∆ х = хВ – хА = - 40 – 20 = - 60,0 Так как знаки приращений отрицательные, то линия лежит в III четверти, где дирекционный угол будет равен: rAB = αАВ - 180˚ => αАВ = 180+ rAB Румб линии rAB находим по формуле: tg rАВ = По таблице находим значение угла для tg rАВ =1,5 => rАВ =56˚19', тогда αАВ = 180˚ + 56˚19' = 236˚19' Длину отрезка АВ находим по формуле: sАВ =
Задачи для самоконтроля: 1. Определить координаты точки В: хВ и уВ., если длина линии АВ sAB = 120м, координаты точки А хА = - 10,5м, уА = - 22,0м. дирекционный угол линии АВ αАВ = 225˚35'.
2. Определить длину линии DС sDC и ее дирекционный угол αDC, если координаты начальной и конечной точек равны: хD = 22,5м, уD = - 20,0м хC = 10,0м, уC = 30,0м свои решения подтвердить чертежами в масштабе 1:1000
ЛЕКЦИЯ №6 |
||||||||||||||||||||||||||||||
|
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 3003. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||
Пусть (рисунок 5.2) даны прямоугольные координаты хА и уА точки А и полярные координаты s и αАВ точки В
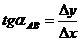, причем в результате вычислений будет найден острый угол (румб). Чтобы по румбу определить величину дирекционного угла нужно сначала выяснить, к какой четверти относится этот угол, что зависит от знаков приращений ∆х и ∆у (см. табл.5.1)
