Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задание 5. Определение устойчивости откоса методомКруглоцилиндрических поверхностей скольжения Определить коэффициент устойчивости откоса, сложенного однородным грунтом с характеристиками g, j, с при заданном положении кривой скольжения в виде дуги окружности с центром в т. О1. Крутизна откоса 1:m, где Исходные данные – по табл. 5.1.
Рис. 5.1. Схема к задаче 3
Таблица 5.1. Исходные данные к задаче 5
Пример

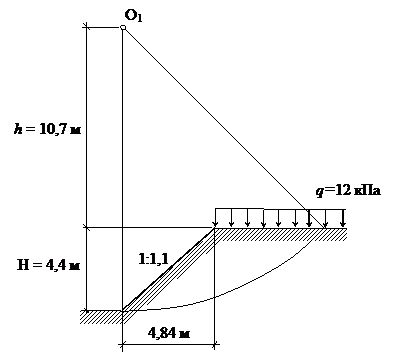
Рис. 5.2. Схема откоса и положение дуги скольжения
Решение
Примем координатную систему xz; радиусом R=(h+H), проводим дугу окружности, выделив массив грунта DAB (рис. 5.3) Координаты точек: О1 (0;-10,7); D (0;4,4); А (m×H;0) или А (4,84;0). Из Δ ОО1В имеем
Тогда
Рис. 5.3. Схема деления массива на отсеки
Решение проводим по алгоритму: 1. Делим массив DAB на 6 отсеков, нумеруя их снизу вверх: 2. Записываем уравнение окружности с центром в т. О1 (0;-10,7) x2+(z+10,7)2=R2 или x2+z2+21,4z – 113,52=0. 3. Вычисляем правые высоты отсеков. Для отсека №1, используя уравнение окружности, при x1=1,6 м, получаем z1=4,32 м. Тогда
Аналогично для отсека № 2 при x2=3,2 м получаем z2=4,06. Правая высота отсека
Для отсека №3 x3=4,84 м, z3=3,6 м и
Для 4 – 6 отсеков соответственно имеем: x4=6,74 м, z4 = h4=2,81 м; x5=8,64 м, z5 = h5 =1,68 м; x6=10,65 м, z6 = h5 = 0 м. 4. Определяем площади отсеков, пренебрегая кривизной поверхности скольжения в силу незначительной разницы в длине между хордой и дугой в пределах одного отсека:
5. Определяем вес отсеков (l = 1 м); для № 4, № 5 и № 6 учитываем Q1=S1×g = 1·17,5=19,25 кН/м; Q2 = S2×g = 3,15·17,5=55,13 кН/м; Q3 = S3×g = 5,06·17,5=88,55 кН/м; Q4 = S4×g +q×b4 = 6,09·17,5+12·1,9=129,38 кН/м; Q5 = S5×g +q×b5 = 4,27·17,5+12·1,9=97,53 кН/м; Q6 = S6×g +q×b6 =1,69·17,5+12·2,01=53,70 кН/м. Равнодействующие Qi считаем приложенными в точках пересечения соответствующего участка дуги скольжения и вертикальной линии, проходящей через центр тяжести отсека, т.е. в точках с абсциссами:
6. Определяем центральные углы ai между вертикалью и радиусом в точке приложения веса отсека по формуле
7. Центральный угол, соответствующий дуге DB:
Длина дуги кривой скольжения определяется из соотношения
Силы Qi раскладываем на две составляющие: нормальную Ni к заданной поверхности и касательную Ti, учитывая также сцепление грунта по всей поверхности скольжения. Составляем таблицу для расчета коэффициента устойчивости.
Таблица 5.2. Определение составляющих сил от веса отсеков
Рассчитываем коэффициент устойчивости для принятого очертания поверхности скольжения как отношение момента удерживающих сил (к которым относится сила трения и сцепление) к моменту сил сдвигающих (касательная составляющая веса отсеков):
Вывод. Для заданного положения поверхности скольжения откос устойчив, т. к. Kуст=2,83 > 1. На практике условие устойчивости должно выполняться для минимального значения коэффициента устойчивости, рассчитанного для наиболее опасной возможной поверхности скольжения.
Задание 6. Определение активного и пассивного давлений грунта На подпорную стенку Построить эпюры активного и пассивного давлений грунта на подпорную стенку с гладкими вертикальными гранями и горизонтальной поверхности засыпки (рис 6.1). Определить равнодействующие давлений, указать точки их приложения и ширину призм обрушения и выпора. Исходные данные – по табл. 6.1.
Рис 6.1. Схема к задаче 4
Таблица 6.1. Исходные данные к задаче 6
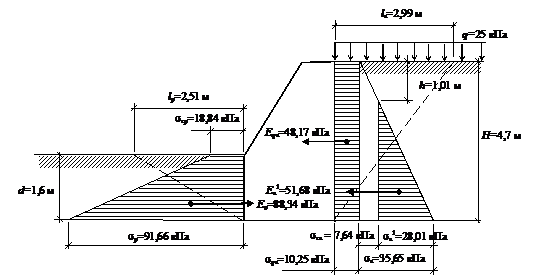
Пример Грунт имеет характеристики: γ = 18,5 кН/м3, φ=25 °, с = 6 кПа. Передняя и задняя грани стенки гладкие вертикальные. Высота задней грани Н=4,7 м, передней – d=1,6 м. На горизонтальной поверхности засыпки приложена равномерно распределенная нагрузка q = 25 кПа. Построить эпюры активного и пассивного давлений грунта на подпорную стенку и определить равнодействующие давлений, указав точки их приложения и ширину призм обрушения и выпора (рис. 6.2).
Рис 6.2. Схема подпорной стенки Решение Подпорная стенка, поддерживая грунт от обрушения, испытывает с его стороны давление, которое принято называть активным. Активное давление, воздействуя на стенку, вызывает ее смещение, что приводит к возникновению сопротивления грунта с другой стороны. Это сопротивление называется пассивным давлением. В первом случае вертикальное напряжение sz = s1 = max, а горизонтальное напряжение sx = sa = min– активное давление, во втором sz = s3 = min, а sx = sp = max – пассивное давление. Активное давление грунта на абсолютно гладкую (отсутствует трение) подпорную стенку без учета сцепления грунта определяется по формуле
где g - удельный вес грунта; z – глубина точки, в которой определяется давление;
Активное давление грунта на нижней грани подпорной стенки, т.е. на глубине z = H: σa = γ·H·λа = 18,5·4,7·0,41 = 35,65 кПа. Наличие сцепления уменьшает активное давления на величину
В этом случае эпюра активного давления начинается на глубине
При действии по поверхности засыпки сплошной равномерно распределённой нагрузки q активное давление грунта
Равнодействующая активного давления
Равнодействующая от давления Пассивное давление на нижней грани подпорной стенки определяется по формуле:
где
Равнодействующая пассивного давления
Точка приложения пассивного давления находится на расстоянии Определяем размеры призм обрушения и выпора:
Строим эпюры активного и пассивного давлений грунта на подпорную стенку.
Рис 6.3. Эпюра активного и пассивного давлений грунта на подпорную стенку
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 573. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
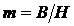 ; откос нагружен равномерно распределенной нагрузкой q.
; откос нагружен равномерно распределенной нагрузкой q.
 Откос сложен однородным грунтом с характеристиками:
Откос сложен однородным грунтом с характеристиками: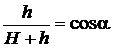 , откуда
, откуда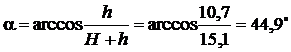 .
.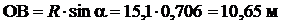 , а т. В имеет координаты (10,65;0).
, а т. В имеет координаты (10,65;0).
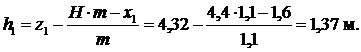
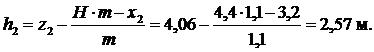
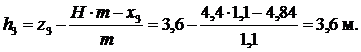
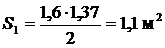 ;
; 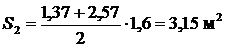 ;
; 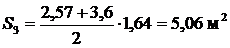 ;
; 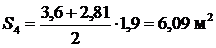 ;
;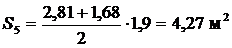 ;
; 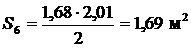 .
.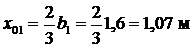 ;
; 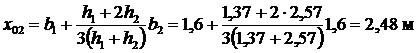 ;
;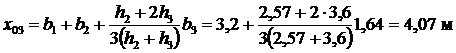 ;
;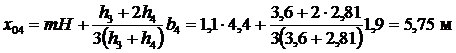 ;
;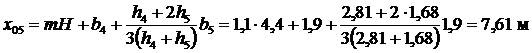 ;
;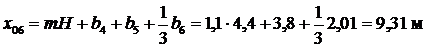 .
. :
: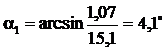 ;
; 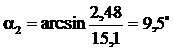 ;
; 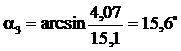 ;
; 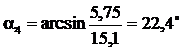 ;
;  ;
; 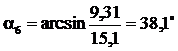 .
. .
.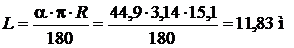 .
.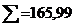
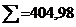
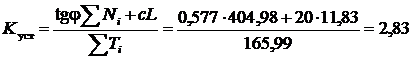 .
.

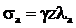 ,
,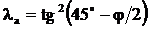 – коэффициент активного давления:
– коэффициент активного давления: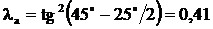 .
.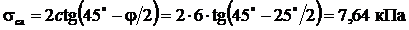 .
.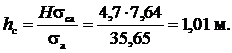
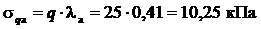 .
.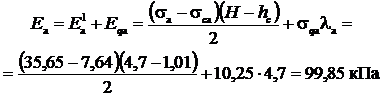
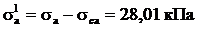 приложена в центре тяжести эпюры , т.е. на расстоянии H/3 = 1,57 м, равнодействующая от давления sqa – на расстоянии H/2 = 2,35 м от нижней грани подпорной стенки.
приложена в центре тяжести эпюры , т.е. на расстоянии H/3 = 1,57 м, равнодействующая от давления sqa – на расстоянии H/2 = 2,35 м от нижней грани подпорной стенки.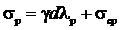 ,
, – коэффициент пассивного давления;
– коэффициент пассивного давления; 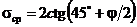 .
.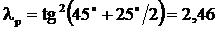 ;
;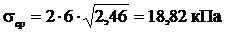 ;
;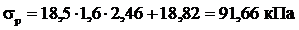 .
.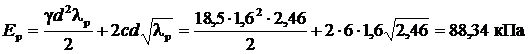 .
. от нижней грани подпорной стенки.
от нижней грани подпорной стенки.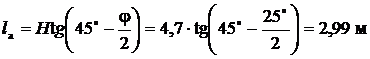 ,
,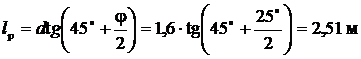 .
.