
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Тема 3. Линейные функционалы и операторы
Глава 1. Линейные функционалы. § 1. Непрерывные линейные функционалы. 1.1. Определение линейного функционала. Def Пусть Def Функционал называется линейным, если 1) аддитивности: 2) Однородности:
1.2. Примеры линейных функционалов № 1. Пусть № 2 В № 3. В № 4. В
№ 5.
1.3. Определение непрерывного функционала. Def В нормированном пространстве функционал Def Функционал Если
§ 2 Связь между непрерывностью и ограниченностью. Лемма. Если линейный функционал непрерывен в одной точке, то он непрерывен всюду на Таки образом, проверять непрерывность линейного функционала достаточно в одной точке, например в 0.  Нет определения ограниченного функционала
Теорема 1. Для того, чтобы линейный функционал Теорема 2. Линейный функционал непрерывен тогда и только тогда когда он ограничен.
§ 3. Норма функционала. 3.1. Определение нормы Def Нормой линейного непрерывного функционала Равносильные определения Из последнего определения следует очевидное свойство
3.2. Примеры вычисления нормы. Вычислим нормы функционалов из п.1.2. № 1. (План 1) оцениваем 2) делим на 3) подбираем элемент
№2
Т.е. № 3 Наш оператор линеен, непрерывен
Если
§ 4 Продолжение линейного функционала. 4.1. Продолжение по непрерывности. Если в линейном пространстве Данный вопрос решается легко, если Заметим, что данное продолжение, является продолжением с сохранением нормы.
4.2. Продолжение функционала, заданного на подпространстве. Теорема Хана-Банаха. Более сложный случай возникает, если функционал задан на подмножестве Теорема Хана-Банаха. Пусть 2)
4.3. Следствие из теоремы Хана-Банаха. Следствие 1. Следствие 1 утверждает существование в любом линейном нормированном пространстве линейного непрерывного функционала, не равного тождественно нулю.. Следствие 3. Пусть Следствие 4. (Об отделимости элемента и подпространства) Пусть Тогда 1) 2) 3) Следствие 5 (Критерий замкнутости системы). Для того чтобы система элементов
§ 5. Сопряженное пространство. Пусть
Примем за норму элемента Т.к. Def Те пространства для которых В этом случае Вложение
§ 6. Сильная и слабая сходимости. 6.1. Сильная сходимость Def Последовательность функционалов Теорема. Сопряженное пространство
6.2. Теорема Банаха-Штейнгауза (Критерий слабой сходимости) Теорема. Если последовательность
6.3. Слабая сходимость. Def Последовательность Теорема 1 (Критерий слабой сходимости для функционалов) Для того, чтобы последовательность 1о. Последовательность 2о. Заметим, что из теоремы Банаха-Штейнгауза следует важный результат. Теорема 2. Пространство
6.4. Связь между сильной и слабой сходимостью. Из сильной сходимости последовательности функционалов следует ее слабая сходимость
Из слабой сходимости последовательности функционалов следует сильная только в случае конечномерных пространств. В общем случае это неверно.
§ 7. Общий вид линейных функционалов. 7.1. Общий вид линейного функционала в гильбертовом пространстве. Теорема Рисса. Теорема Рисса. Всякий линейный непрерывный функционал Теорема Рисса означает, что сопряженное пространство 7.2. Общий вид линейного функционала в № 1
№ 2.
№ 3
№ 4
№ 5.
Заметим, что при
7.3. Общий вид линейного функционала в Теорема (Ф.Рисса) всякий линейный непрерывный функционал
При этом Эта теорема устанавливает изоморфизм
Глава II. Линейные операторы. § 1. Непрерывные линейные операторы 1.1. Определение линейного оператора. Def оператор 1) аддитивен, т.е. 2) Однороден, т.е. В дальнейшем будем писать также
1.2. Определение непрерывного оператора Def Оператор Def Если оператор непрерывен в каждой точке Теорема. Если линейный оператор
1.3. Примеры линейных операторов № 1. Пусть Такой оператор, переводящий каждый элемент пространства в себя, называется единичным оператором. № 2. Пусть № 3. Пусть № 4. Общий вид линейного оператора, переводящего конечномерное пространство в конечномерное. Пусть
§ 2. Связь между непрерывностью и ограниченностью Def Оператор Теорема. Для того чтобы линейный оператор был непрерывен
§ 3. Норма оператора. 3.1. Определение нормы оператора. Def Пусть Равносильные определения
3.2. Примеры вычисления нормы Вычислим нормы операторов из п. 1.3. №1. №2. Так как
Равенство достигается при №3
Единица не достигается, но
§ 4. Продолжение линейного оператора В отличие от линейного функционала, линейный оператор может продолжаться только по непрерывности, т.е. теорем Хана-Банаха места не имеет. Если линейный ограниченный оператор Данное продолжение единственно.
§ 5. Пространство линейных ограниченных операторов. 5.1. Полнота пространства операторов. Пусть Действуя по аналогии с функционалами, введем в
Каждому элементу этой совокупности Теорема. Множество Если же
5.2. Сходимость последовательности операторов. Def Последовательность Def Сходимость по норме называют также равномерной сходимостью. Если Def Последовательность Def Последовательность Заметим, что сходимости связаны следующими соотношениями
В обратную сторону неверно. Теорема 1. Пространство Основную роль в доказательстве этого факта играет Теорема 2 (Банаха-Штейнгауза; принцип равномерной ограниченности). Пусть
5.3. Функции операторов Вначале введем произведение операторов Если Тогда В случае, если Учтем, что операция умножения свойством коммутативности не обладает, т.е. Теперь в
Тогда, чтобы определить функции операторов воспользуемся стандартными разложениями
(Ряды сходятся, так как сходятся ряды из норм, а пространство
§ 6. Обратный оператор. 6.1. Понятие обратного оператора. Решение систем линейных алгебраических уравнений, линейных интегральных уравнений, а также некоторых задач для обыкновенных дифференциальных уравнений и уравнений с частными производными сводится к вопросу о существовании и единственности решения линейных операторных уравнений вида Пусть задан линейный оператор Обратное отображение, обозначаемое Предположим, что оператор Def Множество тех Теорема. Линейный оператор
6.2. Односторонние обратные операторы Def Линейный оператор В этом случае решение Def Линейный оператор Def Если линейный оператор
6.3. Теорема 1. Линейный оператор
Теорема 2. Пусть Теорема 3. Множество обратимых операторов
6.4. Теорема Банаха об обратном операторе. Теорема. Если Следствие 1. (Теорема об открытом отображении) Линейное непрерывное отображение Следствие 2. (Лемма о тройке). Пусть
§ 7. Сопряженный оператор. 7.1. Определение сопряженного оператора. Рассмотрим непрерывный линейный оператор Обозначив
Def Это соотношение и примем за определение сопряженного оператора.
7.2. Свойства сопряженного оператора. 1. Оператор 2. 3. 4. 5. 6.
7.3. Унитарный оператор. Def Пусть Свойства унитарного оператора 1о. Унитарный оператор линеен и ограничен. 2о. Унитарный оператор имеет обратный, который также унитарен. 3о. Произведение двух унитарных операторов есть унитарный оператор. 4о. Оператор 5о. Унитарный оператор отображает Точка 1) 2) Тогда из теоремы об обратном операторе существует обратный оператор
7.4. Понятие сопряженного оператора.
Теорема 1. Если Теорема 2. Пусть Теорема 3. Если
§ 8. Спектр оператора. Резольвента. 8.1. Конечномерный случай. Пусть Итак, в конечномерном пространстве существуют две возможности: 1) Уравнение 2) существует ограниченный оператор
8.2. Резольвентное множество Определение Комплексное число (точка комплексной плоскости) называется регулярной точкой оператора Совокупность всех регулярных точек оператора Если |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 269. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
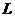 - линейное нормированное пространство. Числовую функцию
- линейное нормированное пространство. Числовую функцию  , определенную на
, определенную на  .
. .
. .
. есть
есть  -мерное пространство с элементами
-мерное пространство с элементами  и
и  - произвольный набор из
- произвольный набор из  - линейный функционал в
- линейный функционал в 

 , где
, где  некоторая фиксированная непрерывная функция на
некоторая фиксированная непрерывная функция на  . Линейность следует из основных свойств операции интегрирования.
. Линейность следует из основных свойств операции интегрирования. , т.е. фиксируем точку
, т.е. фиксируем точку  и для каждой функции
и для каждой функции  функционал равен значению этой функции в данной точке. Этот функционал обычно записывают через
функционал равен значению этой функции в данной точке. Этот функционал обычно записывают через  -функцию Дирака
-функцию Дирака , где
, где  всюду, кроме
всюду, кроме  , и интеграл от которой равен 1.
, и интеграл от которой равен 1. Пусть
Пусть 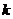 - фиксированное число: Для каждого
- фиксированное число: Для каждого  положим
положим  .
. называется непрерывным, если из условия
называется непрерывным, если из условия  следует
следует 
 и
и 
 такая окрестность
такая окрестность  , что
, что  при
при  .
.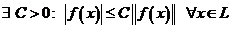
 , на которой функционал
, на которой функционал  ,
, .
. .
. , где
, где  .
. , пытаясь выделить
, пытаясь выделить 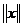
 , на котором это значение достигается)
, на котором это значение достигается)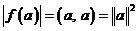 , т.е.
, т.е.  , т.е.
, т.е.  .
.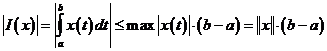 .
. причем при
причем при  достигается равенство
достигается равенство  .
. .
. ограничен
ограничен .
. знакопостоянна на
знакопостоянна на  . Если
. Если  . Но эта функция не принадлежит
. Но эта функция не принадлежит  .
. , то естественно возникает вопрос о его продолжении на все пространство с сохранением определенных свойств. Т.е. требуется построить новый функционал, определенный уже на всем пространстве, обладающий определенными свойствами и совпадающий на
, то естественно возникает вопрос о его продолжении на все пространство с сохранением определенных свойств. Т.е. требуется построить новый функционал, определенный уже на всем пространстве, обладающий определенными свойствами и совпадающий на  с ранее заданным.
с ранее заданным.
 ,
,  . Положим
. Положим  .
. , если
, если 
 .
. ,
,  ,
,  .
. , то
, то  .
. и
и  .
.

 .
. была замкнутой необходимо и достаточно, чтобы из того, что функционал
была замкнутой необходимо и достаточно, чтобы из того, что функционал 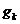 следовало, что
следовало, что  .
. - множество всех линейных непрерывных функционалов, определенных на
- множество всех линейных непрерывных функционалов, определенных на  ;
; 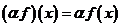 .
. норму
норму  соответствующего функционала. Поскольку она также удовлетворяет всем аксиомам нормированного пространства, то
соответствующего функционала. Поскольку она также удовлетворяет всем аксиомам нормированного пространства, то  , непрерывных линейных функционалов на
, непрерывных линейных функционалов на  называются рефлексивными.
называются рефлексивными. и
и 
 (
(  )
) желательно определять равенством
желательно определять равенством  сходится к элементу
сходится к элементу  при
при  .
. , то последовательность норм
, то последовательность норм  этих функционалов, также ограничена.
этих функционалов, также ограничена. называется слабо сходящейся к элементу
называется слабо сходящейся к элементу  .
. линейных функционалов слабо сходилась к линейному функционалу
линейных функционалов слабо сходилась к линейному функционалу  для любого
для любого  из некоторого множества
из некоторого множества 

 имеет вид
имеет вид  , где
, где  - некоторый элемент из
- некоторый элемент из  изоморфно самому
изоморфно самому  и
и  (
(  ).
).
 изоморфно
изоморфно 

 , где
, где 
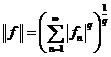 или
или  .
. ,
,  изоморфно пространству
изоморфно пространству  всех ограниченных последовательностей с нормой
всех ограниченных последовательностей с нормой 

 .
. - пространство стремящихся к нулю последовательностей
- пространство стремящихся к нулю последовательностей  с нормой
с нормой 
 изоморфно пространству
изоморфно пространству 
 ,
,  изоморфно
изоморфно 
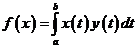 , где
, где 
 .
.
 изоморфно пространству
изоморфно пространству  - ограниченных на
- ограниченных на  - почти всюду на
- почти всюду на  .
.
 и
и  т.е.
т.е.  и
и  , где
, где  - некоторая функция ограниченной вариации на
- некоторая функция ограниченной вариации на  .
. и
и  - пространства функций с ограниченным изменением.
- пространства функций с ограниченным изменением. , определенный на пространстве
, определенный на пространстве  и принимающий значения в пространстве
и принимающий значения в пространстве  , называется линейным, если этот оператор
, называется линейным, если этот оператор
 .
. ,
, 
 .
.
 называется непрерывным в точке
называется непрерывным в точке  , если
, если  при
при  (здесь
(здесь  ) или, что равносильно: если
) или, что равносильно: если 
 .
. , где
, где  - линейное нормированное пространство.
- линейное нормированное пространство.
 , где
, где  непрерывная фиксированная функция, такой оператор называется оператором умножения на функцию
непрерывная фиксированная функция, такой оператор называется оператором умножения на функцию  - оператор дифференцирования
- оператор дифференцирования 
 , где
, где  -пространство непрерывно дифференцируемых функций на
-пространство непрерывно дифференцируемых функций на  .
.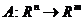 , тогда
, тогда 
 , такой что
, такой что  . Ясно, что оператор
. Ясно, что оператор 

 .
.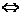 чтобы он был ограничен.
чтобы он был ограничен. называется нормой оператора
называется нормой оператора 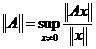 .
. .
. .
. .
. , то
, то 

 .
.
 .
. , т.к. к ней можно сколь угодно приблизиться, например, на последовательности
, т.к. к ней можно сколь угодно приблизиться, например, на последовательности 
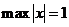 ,
,  , поэтому
, поэтому  - плотном множестве линейного нормированного пространства
- плотном множестве линейного нормированного пространства  можно продолжить по непрерывности на все пространство
можно продолжить по непрерывности на все пространство  совокупность всех линейных непрерывных операторов, действующих из
совокупность всех линейных непрерывных операторов, действующих из 
 ,
,  .
. .
. назовем сходящейся по норме к оператору
назовем сходящейся по норме к оператору  .
. .
. , если
, если  .
. .
. ограничена.
ограничена. ,
,  , то
, то  .
. - линейный ограниченный оператор из
- линейный ограниченный оператор из  .
. , то здесь можно определить операторы и
, то здесь можно определить операторы и  .
. .
. можно ввести любую степень оператора
можно ввести любую степень оператора ,
, 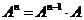 ,
,  .
. ,
,  ,
,  , …
, … .
. , причем, его область определения
, причем, его область определения  , а область значений
, а область значений  .
. , называется обратным оператором.
, называется обратным оператором. на
на  взаимно однозначно. В этом случае существует обратный оператор
взаимно однозначно. В этом случае существует обратный оператор  , называется ядром линейного оператора
, называется ядром линейного оператора  .
. .
. такой, что
такой, что 
 единственно однако вопрос о существовании решения остается открытым.
единственно однако вопрос о существовании решения остается открытым. такой, что
такой, что  ,
,  .
. и
и  такая, что
такая, что 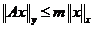
 , то оператор
, то оператор  непрерывно обратим, справедливо равенство
непрерывно обратим, справедливо равенство  , где ряд сходится равномерно, и справедлива оценка
, где ряд сходится равномерно, и справедлива оценка  .
. открыто.
открыто. - банаховы пространства и
- банаховы пространства и  - непрерывные линейные операторы из
- непрерывные линейные операторы из  , соответственно, причем
, соответственно, причем  ). Если при этом
). Если при этом  , то
, то 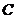 , отображающий
, отображающий  .
. - линейный функционал, определенный на
- линейный функционал, определенный на  .
. через
через  получим
получим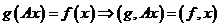 или
или  .
. линеен
линеен



 .
. отображает
отображает  выполняется равенство
выполняется равенство  (т.е. унитарный оператор сохраняет скалярное произведение).
(т.е. унитарный оператор сохраняет скалярное произведение). [это следует из
[это следует из  ].
]. с сохранением нормы, т.е.
с сохранением нормы, т.е.  . [это следует из определения, т.к.
. [это следует из определения, т.к.  ].
]. называется регулярной, если
называется регулярной, если

 называемый резольвентой.
называемый резольвентой. пусть
пусть  . т.е.
. т.е.  выполняется равенство
выполняется равенство  .
. обозначается
обозначается  .
. ,
,  , то
, то 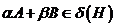
 .
. , то
, то  .
. . Число
. Число  называется собственным значением оператора
называется собственным значением оператора  имеет ненулевые решения
имеет ненулевые решения  . Совокупность всех собственных значений называется спектром оператора
. Совокупность всех собственных значений называется спектром оператора  обратим. При этом
обратим. При этом  .
. , то оператор
, то оператор  из
из  называется резольвентой оператора
называется резольвентой оператора