
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Тема 1. Метрические пространстваГЛАВА 1. МНОЖЕСТВА
§ 1. Операции над множествами Под множеством мы будем понимать какую-либо совокупность элементов. Любое множество содержит Подмножества, отличные от самого множества и от
Аналогично определяется объединение и пересечение любого (конечного или бес конечного) числа множеств.
Операции сложения и пересечения коммутативны и ассоциативны
§ 2. Мощность множеств 2.1. Конечные и счетные множества Среди множеств есть такие, в которых мы знаем количество элементов. Эти множества содержат конечное, хотя, может быть, и неизвестное нам число. Простейшим бесконечным множеством является множество натуральных чисел. Назовем счетным множеством всякое множество, элементы которого можно биективно сопоставить с натуральным рядом. Бесконечное множество, не являющееся счетным, называется несчетным множеством. Свойства счетных множеств. 1) Всякое подмножество счетного множества конечно или счетно. 2) Сумма любого конечного или счетного числа множества счетных множеств есть снова счетное множество  3) Всякое бесконечное множество содержит счетное подмножество. DEF Два множества DEF Множество называется счетным, если оно эквивалентно множеству натуральных чисел. Ясно, что два множества, эквивалентны третьему, эквивалентны между собой. В частности, любые два счетных множества эквивалентны между собой.
2.2. Несчетные множества Теорема 1. Множество действительных чисел, заключенных между нулем и единицей несчетно. Приведем примеры несчетных множеств, эквивалентных отрезку 1) Множество всех точек любого отрезка 2) Множество всех точек на прямой 3) Множество всех точек на плоскости 4) Множество всех непрерывных функций одного или нескольких переменных.
2.3. Мощность множества Эквивалентные множества имеют одинаковую мощность. Для конечных множеств мощность равна числу элементов множеств. Мощность любого счетного множества равна мощности множества натуральных чисел. Отрезок Мощностей, промежуточных между счетным и континуумом нет.
Глава 2. Метрические, нормированные и гильбертовы пространства
§ 1. Метрические пространства. Def: Метрическим пространством называется пара 1) 2) 3) Обычно метрическое пространство обозначают 1.2. Непрерывные отображения Пусть Def. Это отображение называется непрерывным в точке ( Если отображение непрерывно во всех точках пространства В случае если Если отображение Если В этом случае пространства Если же Изометрия пространств
1.3. Предельные точки. Замыкание. Введем некоторые понятия теории метрических пространств. Открытый шар Аналогично Замкнутый шар Точка Предельная точка может принадлежать, а может и не принадлежать Точка Операция замыкания представляет собой присоединение к
1.4. Сходимость в метрических пространствах. Пусть
1.5. Сепарабельность Пусть Множество Множество Пример: множество рациональных чисел всюду плотно на числовой прямой. Множество Пространства, в которых имеется счетное, всюду плотное подножество называются сепарабельными.
1.5. Открытые и замкнутые множества Def. Множество Теорема 1. Пересечение любого числа и сумма (объединение) любого конечного числа замкнутых множеств есть замкнутое множество. Def. Def. Множество все точки которого внутренние, называется открытым. Теорема 2. Для того, чтобы множество Следствие. Т.к. Из теоремы 1 и из принципа двойственности (пересечение дополнений равно дополнению объединений; объединение дополнений равно дополнению пересечения) следует Теорема 3. Объединение любого и пересечение любого конечного числа открытых множеств есть открытое множество. Def: Класс Def: Борелевской
1.6. Открытые и замкнутые множества на прямой. Структура открытых и замкнутых множеств в том или ином метрическом пространстве может быть весьма сложной. Даже в Однако на прямой, описание всех открытых множеств (а значит и замкнутых) можно проделать теоремой. Теорема. Всякое открытое множество на числовой прямой представляет собой объединение конечного и счетного числа попарно непересекающихся интервалов.
1.8. Полные метрические пространства Def: Последовательность Def: Последовательность Def: Если в метрическом пространстве
1.9. Теорема о вложенных шарах и теорема Бэра. В анализе широко используется лемма о вложенных отрезках. В теории метрических пространств аналогичную роль играет теорема. Теорема о вложенных шарах. Для того, чтобы метрическое пространство было полным, необходимо и достаточно, чтобы в нем всякая последовательность вложенных друг в друга замкнутых шаров, радиусы которых стремятся к 0 имела непустое пересечение. Теорема Бэра. Полное метрическое пространство
1.10. Пополнение метрического пространства Если пространство Теорема. Для любого метрического пространства 1) 2) 3) Пространство
§ 2. Нормированные пространства. 2.1. Линейные пространства. Определение и примеры. Def Непустое множество 1о. 2о. 3о. 4о. 5о. 6о. 7о. 8о. Примеры линейных пространств 1) Def Элементы Def Бесконечная система элементов линейно независима, если любая ее конечная подсистема линейно независима. Def Базисом в Def Если в
2.2. Подпространства Def Непустое множество Def Подпространство, 1) отличное от
2.3. Фактор- пространства (по подпространству). Пусть Совокупность всех таких классов смежности мы назовем фактор-пространства При этом линейные операции в фактор-пространстве Т.е. каждое фактор-пространство Заметим, что если размерность
2.4. Нормированные пространства. Определения и примеры Def Отображение 1) 2) 3) Как правило, вместо Def Линейное пространство с заданной нормой называется нормированным пространством. Каждое нормированное пространство становится метрическим, если в нем ввести расстояние Def Полное нормированное пространство называется банаховым пространством.
§ 3. Гильбертово пространство. 3.1. Предгильбертово пространство. Def Говорят, что в комплексном линейном пространстве 1) 2) 3) Def Линейное пространство со скалярным произведением называется предгильбертовым. Def Конечномерное вещественное предгильбертово пространство называют евклидовым, а комплексное – унитарным. Предгильбертово пространство становится линейным нормированным, если в нем ввести норму Для того, чтобы нормированное пространство было предгильбертовым, необходимо и достаточно, чтобы выполнялось тождество параллелограмма
3.2. Гильбертово пространство. Поскольку предгильбертово пространство является линейным нормированным пространством, то в нем можно рассматривать понятие полноты по норме, определенной скалярным произведением. Def Предгильбертово пространство, полное относительно нормы Теорема. Любые два сепарабельных гильбертовых пространства изоморфны между собой.
3.3. Подпространства гильбертова пространства, ортогональные дополнения. Def Линейным многообразием в гильбертовом пространстве Def Замкнутое линейное многообразие называется подпространством. Всякое подпространство гильбертова пространства либо является конечномерным евклидовым пространством либо евклидовым пространством. Теорема. В каждом подпространстве Пусть Def Подпространство Из предыдущей теоремы легко следует Теорема. Если Следствие 1. Ортогональное дополнение к ортогональному дополнению линейного пространства Следствие 2. каждая ортогональная нормированная система может быть расширена до системы, полной в Def Если каждый вектор Понятие прямой суммы может быть обобщено на любое конечное или даже счетное число подпространств. Def говорят, что
если 1) подпространства 2) каждый элемент
если число подпространств бесконечно, Если такое представление
Глава 3. Принцип сжимающих отображений § 1. Принцип сжимающих отображений Def Отображение
При этом точка Теорема (Принцип сжимающих отображений). Всякое сжимающее отображение в полно метрическом пространстве имеет одну и только одну неподвижную точку. Неподвижная точка
§ 2. Применение к интегральным уравнениям. 2.1. Уравнения Фредгольма. Этот материал (интегральные уравнения) будет изучаться на IV курсе, но применять метод последовательных приближений к решению интегральных уравнений мы можем сейчас, на практике.
(если слева 0, где Из принципа сжимающих отображений имеем, что для любого
2.2. Уравнение Вольтерра. Интегральное уравнение типа Вольтерра
(в отличие от Фредгольма верхний предел в интеграле переменный). Можно считать его частным случаем уравнения Фредгольма, если доопределить
Глава 4. Компактность в метрических пространствах. § 1. Понятие компактности. Фундаментальную роль в анализе играет следующий факт, известный под названием Лемма Гейне-Бореля. Из любого покрытия отрезка Def Метрическое пространство Теорема. Замкнутое подмножество компактного пространства компактно. Def Множество
§ 2. Компактность в метрических пространствах 2.1. Полная ограниченность. Def Пусть Def Множество Заметим, что полная ограниченность есть необходимое условие компактности метрического пространства. Однако имеет место следующая теорема. Теорема 1. (Хаусдорфа) Для того, чтобы метрическое пространство 1) вполне ограниченным 2) полным. Следствие: Компактное пространство Укажем на связь между полной ограниченностью и предкомпактностью. Теорема 2. Для того, чтобы множество 2.2. Теорема Арцела-Асколи. Вопрос о компактности множества В В пространстве Теорема Арцела-Асколи. Для того, чтобы множество 1) равномерно ограничено 2) равностепенно непрерывно. Def. Множество Def. Множество
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 326. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 в качестве подмножества.
в качестве подмножества. - объединение множеств – множество, состоящее из элементов, принадлежащих хотя бы одному из множеств
- объединение множеств – множество, состоящее из элементов, принадлежащих хотя бы одному из множеств  и
и  .
.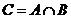 - пересечение множеств – множество, состоящее из всех элементов, принадлежащих как
- пересечение множеств – множество, состоящее из всех элементов, принадлежащих как 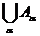 - совокупность элементов, каждый из которых принадлежит хотя бы одному из множеств
- совокупность элементов, каждый из которых принадлежит хотя бы одному из множеств 
 - совокупность элементов, каждый из которых принадлежит каждому из множеств
- совокупность элементов, каждый из которых принадлежит каждому из множеств 



 Разность множеств – множество, состоящее из элементов
Разность множеств – множество, состоящее из элементов  Симметрическая разность – объединение двух разностей.
Симметрическая разность – объединение двух разностей. и
и  называются эквивалентными, если между их элементами можно установить взаимно однозначное соответствие (биекцию)
называются эквивалентными, если между их элементами можно установить взаимно однозначное соответствие (биекцию)
 или интервала
или интервала 
 .
. , состоящая из некоторого множества (пространства)
, состоящая из некоторого множества (пространства)  элементов (точек) и расстояния, т.е. однозначной неотрицательной действительной функции
элементов (точек) и расстояния, т.е. однозначной неотрицательной действительной функции 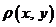 и определенной для любых
и определенной для любых  и
и  из
из  .
. (симметрия).
(симметрия). (неравенство треугольника)
(неравенство треугольника) два метрических пространства и
два метрических пространства и  - отображение пространства
- отображение пространства  , если
, если 
 -расстояние в
-расстояние в 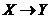 взаимно однозначно, то
взаимно однозначно, то  обратное отображение
обратное отображение  .
. непрерывны), то она называется гомеоморфным отображением является гомеоморфизмом.
непрерывны), то она называется гомеоморфным отображением является гомеоморфизмом. (одна функция для
(одна функция для  - метрические пространства.
- метрические пространства. 

 -окрестности точки
-окрестности точки 
 . Множество
. Множество  ограничено, если
ограничено, если  .
. называется предельной точкой множества
называется предельной точкой множества  много точек из
много точек из  нет точек из
нет точек из  .
. ,
,  ,… - последовательность точек в метрическом пространстве
,… - последовательность точек в метрическом пространстве 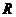 . Говорят, что
. Говорят, что  сходится к точке
сходится к точке 
 такое, что
такое, что  содержит все
содержит все  с
с  . Точка
. Точка  , если
, если 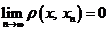 .
. .
. .
. содержится другой шар
содержится другой шар  , такой что
, такой что  .
. , т.е
, т.е  (целиком содержащаяся)
(целиком содержащаяся) (до всего пространства
(до всего пространства  - подмножеств пространства
- подмножеств пространства  .
. называется фундаментальной, если
называется фундаментальной, если  .
. .
. существует полное метрическое пространство
существует полное метрическое пространство  такое, что
такое, что

 .
.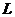 называется линейным (или векторным) пространством, если в нем определены операции сложения и умножения на число, обладающие следующими свойствами
называется линейным (или векторным) пространством, если в нем определены операции сложения и умножения на число, обладающие следующими свойствами  ,
,  (действительное линейное ) (или
(действительное линейное ) (или  (коммутативность)
(коммутативность) (ассоциативность)
(ассоциативность) (существование нуля)
(существование нуля) (существование противоположного элемента)
(существование противоположного элемента)



 ; 2)
; 2)  3)
3)  4)
4) 
 называются линейно зависимыми, если существуют такие числа
называются линейно зависимыми, если существуют такие числа  , не все равные 0, что
, не все равные 0, что  (1).
(1). -мерном пространстве называется любая система из
-мерном пространстве называется любая система из  линейного пространства
линейного пространства  .
. .
. .
. ,
,  , а
, а  ,
,  , то классы смежности
, то классы смежности  и
и  определяются как классы, которым принадлежат
определяются как классы, которым принадлежат  и
и  , соответственно).
, соответственно). , а размерность
, а размерность 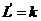 , то размерность
, то размерность  .
. линейного пространства
линейного пространства  называется нормой, если
называется нормой, если  выполнено
выполнено

 (неравенство треугольника)
(неравенство треугольника) пишут
пишут 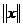 . (Эта величина аналогична длине отрезка).
. (Эта величина аналогична длине отрезка). .
. поставлено в соответствие комплексное число
поставлено в соответствие комплексное число  так, что выполнены следующие аксиомы:
так, что выполнены следующие аксиомы: , причем
, причем 
 (линейность)
(линейность) (эрмитовость).
(эрмитовость).
 .
. назовем совокупность
назовем совокупность 
 , то
, то  .
. , линейное замыкание которой совпадает с
, линейное замыкание которой совпадает с  - множество элементов
- множество элементов  , ортогональных по всем элементам
, ортогональных по всем элементам 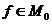
 называется ортогональным дополнением пространства
называется ортогональным дополнением пространства  единственным образом представим в виде
единственным образом представим в виде 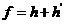 , где
, где  ,
,  .
. .
.

 попарно ортогональны, т.е. любой вектор из
попарно ортогональны, т.е. любой вектор из  , при
, при 
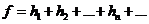
 (*)
(*) - сходится.
- сходится. .
. метрического пространства в себя называется сжимающим, если существует такое число
метрического пространства в себя называется сжимающим, если существует такое число  , что
, что 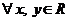
 .
.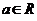 называется неподвижной точкой отображения
называется неподвижной точкой отображения 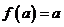 .
. может быть найдена методом последовательных приближений
может быть найдена методом последовательных приближений , где
, где  .
. решения неоднородного линейного интегрального уравнения Фредгольма второго рода, т.е. уравнения
решения неоднородного линейного интегрального уравнения Фредгольма второго рода, т.е. уравнения
 , то однородное)
, то однородное) - ядро, и
- ядро, и  - данные функции, а
- данные функции, а  ,
,  уравнение имеет единственное непрерывное решение. Последовательные приближения к этому решению имеют вид
уравнение имеет единственное непрерывное решение. Последовательные приближения к этому решению имеют вид ,
,  , где в качестве
, где в качестве  можно взять любую непрерывную функцию.
можно взять любую непрерывную функцию.
 при
при  . Но в отличие от Фредгольма, к уравнениям Вольтерра принцип сжимающих отображений (и метод последовательных приближений) применим при всех значениях
. Но в отличие от Фредгольма, к уравнениям Вольтерра принцип сжимающих отображений (и метод последовательных приближений) применим при всех значениях  .
. такая, что
такая, что  . (Множество
. (Множество  существует конечная
существует конечная  критерий компактности имеет вид
критерий компактности имеет вид , такое, что
, такое, что 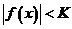
 , для всех
, для всех  .
. , такое, что как только
, такое, что как только 
 сразу
сразу 
 .
.