
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Особенности и нежелательные эффекты
Частота дискретизации и наложение. Выполнению спектрального анализа должна предшествовать передача аналоговых сигналов через фильтр защиты от наложения спектров, задача которого – предотвратить наложение дискретного сигнала после последующего этапа аналого-цифрового преобразования. Наложением называется искажение спектра сигнала при вводе паразитных (побочных) низкочастотных компонентов вследствие объединения недостаточного фильтра защиты от наложения спектров и слишком низкой частоты дискретизации.
Рис. 1. Спектральная плотность амплитуды сигнала с равномерной спектральной плотностью
«Гребешковое искажение», или «эффект частокола». Дискретное преобразование Фурье (ДПФ) выдает гармонические амплитудные и фазовые компоненты, равномерно размещенные по шкале частот. Густота размещения спектральных линий уменьшается с увеличением длины дискретизованного сигнала. Следовательно, если компонент сигнала расположен между двумя соседними частотными гармониками спектра, представить его надлежащим образом нельзя. Энергия такого компонента будет распределена между соседними гармониками, что приведет к искажению близлежащих спектральных «амплитуд». Спектральная плотность амплитуды равномерно распределенного сигнала показана на рис.1. Отметим конечную ширину основных лепестков, центрированных на гармонических частотах, и то, что компонент сигнала на такой негармонической частоте, как fnh, нельзя представить надлежащим образом. Для решения этой проблемы гармонические компоненты должны размещаться более тесно и совмещаться с частотами сигнала. Этого можно достичь, введя в реальные данные дополнительные нули. Эти нули называются дополняющими и нужны для увеличения точности – приближения оцененного спектра к истинному спектру без использования дополнительной информации. Итак, к N данным требуется добавить такое количество нулей N’, чтобы удовлетворялось условие: 
N+N’=2m
в алгоритме двоичного быстрого преобразования Фурье (БПФ), где m – целое. Кроме того, гармоники частоты l/(N+N’–1)Т, где T представляет интервал дискретизации, должны совпадать с частотами сигнала. Чтобы представить максимальное снижение выигрыша от обработки, которое возникает на частотах, расположенных посредине между гармонически связанными частотами, определяется гребешковое искажение (scalloping loss) (ГИ):
где W представляет ДПФ-образ весовой функции, Как уже отмечалось, конечная длина данных ограничивает возможное разрешение по частоте до l/(N – 1)T (Гц). В результате получается грубый спектр, который можно сгладить и сделать непрерывным, используя дополнительные нули. Данный процесс является просто интерполяцией спектральной кривой между соседними гармониками. Действительного улучшения разрешения можно добиться только за счет более длительной реализации. После дополнения N' нулями интервал частот между линиями спектра становится равным l/(N + N' – 1)T (Гц). Исключение тренда. Перед вычислением спектра нужно удалить все тренды в данных, поскольку вектор ошибок, из-за которого к данным добавляются тренды, будет интегрироваться и может породить большие ошибки в оцененном спектре. Просачивание спектральных составляющих и размывание спектра. БПФ, которое применяется к набору дискретных данных, – это не совсем истинное БПФ процесса, из которого получены данные. Это объясняется тем, что процесс непрерывен, тогда как данные имеют начало и конец, которые определяются выбранной реализацией. Для эффективного получения данных, которые представляют сигнал длительностью Ts(s), все дискретные значения в интервале Ts умножаются на единицу, а все данные вне этого интервала умножаются на нуль. Это эквивалентно умножению (или взвешиванию) сигнала на прямоугольный импульс (взвешивающую, или весовую, функцию) ширины Ts и высоты 1. В этом случае выборки данных v(n) равны произведению элементов данных s(n) и значений весовой функции
v(n) =
Произведение во временной области эквивалентно свертке в частотной. Следовательно, БПФ-образ n-й гармоники равен
где Из уравнения следует, что рассчитанный спектр состоит из истинного спектра данных, свернутого со спектром весовой функции. Амплитудный спектр прямоугольного импульса
Здесь Чтобы минимизировать просачивание спектральных составляющих, форма весовой функции выбирается с минимальными уровнями боковых лепестков. К сожалению, это приводит к увеличению ширины основного лепестка, так что он расширяется на соседние боковые лепестки (происходит наложение). Данный эффект имеет место для всех гармоник, а общий результат – наложение спектра сигнала, или размывание. Таким образом, весовые функции и их параметры надлежит выбирать тщательно, чтобы добиться оптимального баланса между разрешением по частоте и статистической точностью оценки спектра.
Рис. 2. Спектральная плотность амплитуды синусоидального сигнала, свернутого с дискретизующей функцией
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 352. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


 – циклическая частота дискретизации,
– циклическая частота дискретизации, 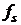 – частота дискретизации, N – число элементов данных, n – номер элемента данных,
– частота дискретизации, N – число элементов данных, n – номер элемента данных, 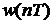 – весовая функция, дискретизованная во временной области.
– весовая функция, дискретизованная во временной области. :
:
 – циклическая частота n-й гармоники,
– циклическая частота n-й гармоники,  – комплексный ДПФ-компонент на частоте
– комплексный ДПФ-компонент на частоте  – ДПФ-образ функции на частоте
– ДПФ-образ функции на частоте  – действительный ДПФ-компонент сигнала на частоте
– действительный ДПФ-компонент сигнала на частоте  записывается следующим образом (данное выражение называется также ядром Дирихле):
записывается следующим образом (данное выражение называется также ядром Дирихле):
 – функция выборки с частотой
– функция выборки с частотой  . Она состоит их основного лепестка и бесконечного числа боковых лепестков с максимумами на 0 Гц и (n+0,5)/Ts Гц соответственно. Теперь амплитудный спектр отдельного синусоидального компонента сигнала на частоте fn включает в себя два импульса на частотах ±fn. Свертка с дискретизирующей функцией дает спектр, изображенный на рис.2. Два импульса преобразовались в две перекрывающиеся выборочные функции. Влияние прямоугольной весовой функции проявилось во введении в вычисленный спектр побочных максимумов (из-за влияния боковых лепестков). Такой эффект будет иметь место для каждого частотного компонента сигнала, так что амплитудный спектр сигнала будет искажен из-за перекрестного сложения и вычитания большого числа боковых и главных лепестков весовых функций. Вследствие этого могут появиться ложные или скрыться истинные максимумы спектра. Данный эффект называется просачиванием спектральных составляющих. Для того чтобы избежать его, данные следует модифицировать – умножить на весовую функцию, форма которой предназначена для снижения влияния боковых лепестков. Подходящая функция равна 1 в центральной точке и сходит на нуль в точках n = 0 и n = N – l. На настоящий момент разработано по крайней мере 23 такие функции.
. Она состоит их основного лепестка и бесконечного числа боковых лепестков с максимумами на 0 Гц и (n+0,5)/Ts Гц соответственно. Теперь амплитудный спектр отдельного синусоидального компонента сигнала на частоте fn включает в себя два импульса на частотах ±fn. Свертка с дискретизирующей функцией дает спектр, изображенный на рис.2. Два импульса преобразовались в две перекрывающиеся выборочные функции. Влияние прямоугольной весовой функции проявилось во введении в вычисленный спектр побочных максимумов (из-за влияния боковых лепестков). Такой эффект будет иметь место для каждого частотного компонента сигнала, так что амплитудный спектр сигнала будет искажен из-за перекрестного сложения и вычитания большого числа боковых и главных лепестков весовых функций. Вследствие этого могут появиться ложные или скрыться истинные максимумы спектра. Данный эффект называется просачиванием спектральных составляющих. Для того чтобы избежать его, данные следует модифицировать – умножить на весовую функцию, форма которой предназначена для снижения влияния боковых лепестков. Подходящая функция равна 1 в центральной точке и сходит на нуль в точках n = 0 и n = N – l. На настоящий момент разработано по крайней мере 23 такие функции.