
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Сила давления на плоскую поверхность
Гидростатический парадокс: давление жидкости не зависит от формы сосуда, а зависит от глубины погружения площади (Г. Галилей). Сила избыточного гидростатического давления на плоскую поверхность дна сосуда площадью
На рис. 13 представлены три сосуда произвольной формы, но имеющие одинаковую площадь дна
Рис 13. Давление на плоскую горизонтальную поверхность
Давление жидкости на наклонную поверхность
Как и любой вектор, сила гидростатического давления, действующая на смоченную часть поверхности S плоской стенки произвольной формы, характеризуется величиной (модулем), направлением и точкой приложения. Предположим, что жидкость действует на наклоненную под углом Определим величину силы

Рис. 14. К вопросу давления жидкости на плоские стенки
На рис. 14 линия АВ – проекция плоской фигуры площадью
Интеграл 
Подставляем значения в выражение силы Р, имеем:
Таким образом, величина абсолютного гидростатического давления равна произведению площади смоченной части плоской стенки на гидростатическое давление в центре тяжести. Центр давления – точка приложения равнодействующей избыточного гидростатического давления, необходима для определения размеров щитов, затворов и других сооружений. Для определения координат
Момент равнодействующей
Сумму моментов
В выражении (31)
Из условия (29) видно, что
тогда координата центра давления
Из рисунка 14: заменим выражение
Известно также, что
где Подставив (34) и (35) в (33), получим
или
где Глубина погружения центра давления может быть определена по формуле:
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 695. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
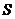 может быть определена по формуле:
может быть определена по формуле: (27)
(27)


 к горизонту стенку ОС (рис. 14).
к горизонту стенку ОС (рис. 14). абсолютного давления на плоскую фигуру АВ, расположенную на стенке ОС (рис. 14) /4/.
абсолютного давления на плоскую фигуру АВ, расположенную на стенке ОС (рис. 14) /4/.
 . Для определения силы гидростатического давления выделим на смоченной поверхности элементарную площадку
. Для определения силы гидростатического давления выделим на смоченной поверхности элементарную площадку  , на которую действует сила
, на которую действует сила



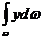 здесь выражает статический момент площади фигуры АВ относительно оси Х, т.е.
здесь выражает статический момент площади фигуры АВ относительно оси Х, т.е.

 ;
;

 (28)
(28) ,
,  центра давления гидростатической силы воспользуемся теоремой Вариньона: если произвольная система сил имеет равнодействующую, то момент этой равнодействующей относительно любой оси равен алгебраической сумме моментов всех сил этой системы относительно той же оси, или
центра давления гидростатической силы воспользуемся теоремой Вариньона: если произвольная система сил имеет равнодействующую, то момент этой равнодействующей относительно любой оси равен алгебраической сумме моментов всех сил этой системы относительно той же оси, или (29)
(29)


 .
.
 относительно оси Х
относительно оси Х (30)
(30) (31)
(31)
 относительно оси Х.
относительно оси Х.
 - момент инерции плоской фигуры АВ относительно оси Х , следовательно
- момент инерции плоской фигуры АВ относительно оси Х , следовательно  (32)
(32) ,
, (33)
(33) (34)
(34) , (35)
, (35)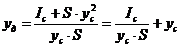 ;
; , (36)
, (36) (37)
(37)