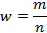Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Построение линейной однофакторной регрессионной модели зависимости результативногопризнакаYот фактораХ.Линейноеоднофакторное уравнениерегрессииимеет вид:
Для расчета коэффициентов строится вспомогательная табл.2.2 (расчетыпроведены с применением пакета MS Excel): Таблица 2.2.
Расчетная таблица для построения и анализалинейной модели парной регрессии.
Расчет коэффициентов уравнения регрессии на основе данных табл.2.2: 
Проверка правильности расчётов (сумма фактических значений результативного признака Y (гр.3) должна совпадать с суммой теоретических значений (гр.7) или незначительно расходиться с ней.) В расчетах наблюдаетсясовпадениесумм: 8505 = 8505.
Вывод. Линейная регрессионная модель связи изучаемых признаков имеет вид уравнения:
Коэффициент регрессии
3. Проверка уравнения регрессии наадекватность 1. Оценка практической пригодности построенной моделисвязи Расчет
Вывод: Критерий практическойпригодности модели связи
2. Оценка статистической значимости (неслучайности) коэффициента
Расчет значения F при n=30, m=2:
Табличное (критическое) значение F-критерия Fтаблимеет общий вид𝐹𝛼; 𝑚−1;𝑛−2, где 𝛼- уровень значимости, m– число коэффициентов уравнения регрессии. Приуровнезначимости 𝛼 =0,05 иm=2: 𝐹𝛼;𝑚−1;𝑛−2=𝐹0,05;1;28=4,2
Таккак Fрасч>Fтабл, то величинанайденногокоэффициентдетерминации
Вывод.Построенное уравнениерегрессии
Расчет коэффициента эластичности
Вывод.Величина коэффициента эластичности𝐾Э= 1.465показывает, чтопри увеличении факторного признака Выручка от продажи продукции на 1% значение результативного признака Прибыль от продажи продукции увеличивается всреднем на1.47 %.
Задание 3. По результатам выполнения задания 1 с вероятностью 0,954 определите: 1) ошибку выборки средней величины выручки от продажи продукции и границы, в которых будет находиться средняя величина выручки предприятий генеральнойсовокупности. 2) ошибку выборки доли предприятий с выручкой от продажи продукции более 𝐱̃ млн. руб. и границы, в которых будет находиться генеральнаядоля.
В решениях используются общепринятые обозначения параметров генеральной и выборочной совокупностей (табл.3.1). Таблица 3.1
Значения параметров, необходимых для решения задачи и рассчитанных в задании 1, представлены в табл. 3.2: Таблица 3.2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 287. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |







 показывает, что при увеличении факторного признака Выручка от продажи продукции на 1 млн руб. значение результативного признака Прибыль от продажи продукции увеличивается всреднем на 0,98825 млн руб.
показывает, что при увеличении факторного признака Выручка от продажи продукции на 1 млн руб. значение результативного признака Прибыль от продажи продукции увеличивается всреднем на 0,98825 млн руб.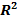 .
. повеличине коэффициента детерминации
повеличине коэффициента детерминации  .
.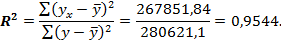
 > 0,5 выполняется. Так как значение
> 0,5 выполняется. Так как значение 
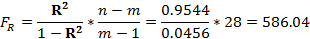
 .признается неслучайной с вероятностью0,95.
.признается неслучайной с вероятностью0,95. можно считать адекватным с надежностью95%.
можно считать адекватным с надежностью95%.