Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Вычисление дирекционных углов и румбов сторон ходаДирекционный угол начального направления (VI-I) вычислить, используя начальный дирекционный угол αо и примычный угол у на пункте I, и заносят его в графу 4 таблицы 2 α6-1 = α0 +180° - γ1 (12) Последующие дирекционные углы вычисляются по правилу: Дирекционный угол стороны теодолитного хода равен дирекционному углу предыдущей стороны плюс левый угол поворота минус (плюс) 180°, т.е. αi = αi-1, +βЛИСПР ±180°. (13) Для правых углов поворота справедлива формула: αi = αi-1 – βПИСП ± 180о (14) В нашем случае правые углы, поэтому вычисляем дирекционные углы всех остальных сторон, руководствуясь следующим правилом: дирекционный угол следующей стороны равен дирекционному углу предыдущей стороны плюс 180о и минус горизонтальный угол, справа по ходу лежащий.
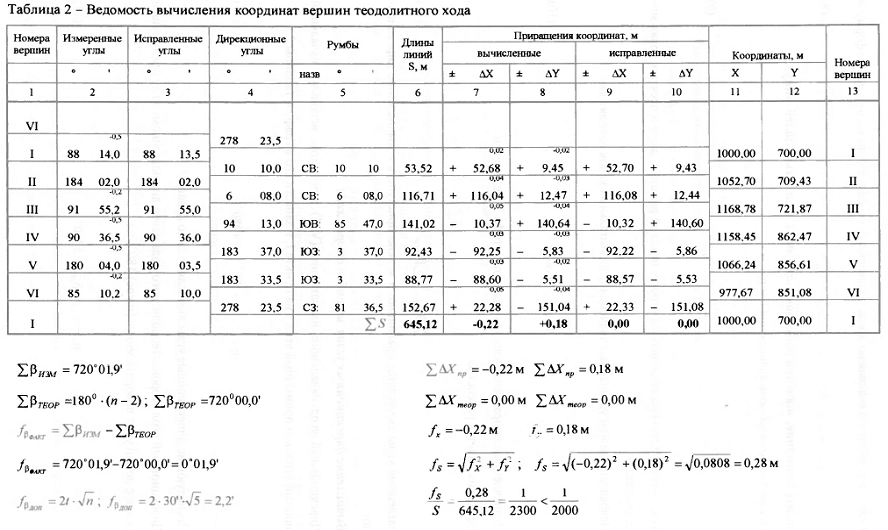
Контроль Вычисление приращений координат. В столбец 6 таблицы уравнивания теодолитного хода записывают горизонтальные проложения сторон (значения берут из таблицы 1). Они должны располагаться в сроках между номерами точек теодолитного хода. Вычисляют приращения координат по формулам: Δx = S cosα. Δy = S sinα (15) Вычисленные приращения записывают в графы 7 и 8, находят практические суммы приращений координат ∑ΔxПР и ∑ΔyПР. Нахождение абсолютной и относительной линейных неувязок хода. Сначала вычисляем неувязки fx и fy в приращениях координат по осям xи y:  fx = ∑ΔxПР - ∑ΔxТ fy = ∑ΔyПР - ∑ΔyТ (16) ΔxТ= xКОН – xНАЧ; ΔyТ =yКОН --yНАЧ– теоретические суммы приращений координат, вычисляемые как разности абсцисс и ординат конечной и начальной точек хода. Абсолютная линейная неувязка теодолитного хода вычисляется по формуле: fS = и записываются до сотых долей метра. Относительная линейная невязка Примечание: Примеры в задании подобраны так, чтобы невязка получалась допустимой. Если эта величина окажется больше 1/2000, значит, в вычислениях допущена ошибка. Чаще всего встречаются ошибки при вычислении дирекционных углов; в знаках приращений координат; при определении значений sin и cos дирекционных углов. Если условие выполняется, то невязки fx и fу распределяют, вводя поправки в вычисленные значения приращений координат. Поправки распределяются прямо пропорционально длинам сторон хода и вводятся со знаком, обратным знаку соответствующей невязки. Vx = - Контроль: ∑YX = -fx; ∑VY = - fY • Поправки записывают над соответствующим приращением красным цветом. Исправленные приращения записываем в графы 9 и 10. Они вычисляются по формулам: ΔХиспр=ΔХвыч+Vx; ΔУИСПР =ΔУВЫЧ+Vy (19) Суммы исправленных приращений должны быть равны соответственно ∑Δхт и ∑δут. Вычисление координат вершин хода. Координаты вершин хода получают путем последовательного алгебраического сложения координат предыдущих вершин хода с соответствующими исправленными приращениями хi=хi-1. + Δхi; yi = yi-1 + Δyi. Контролем правильности вычислений являются полученные по формулам и известные координаты конечной точки.
[!] Вычисления приращений координат выполняют до см, либо, во избежание ошибок округления до мм, т.е. - не более трех знаков после запятой.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 2056. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 αвычкон = αкон.
αвычкон = αкон.
 хода (S - сумма длин сторон) выражается простой дробью с единицей в числителе. Относительная невязка должна быть меньше допустимой величины 1/2000.
хода (S - сумма длин сторон) выражается простой дробью с единицей в числителе. Относительная невязка должна быть меньше допустимой величины 1/2000.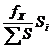 , VY =
, VY =  (18)
(18)