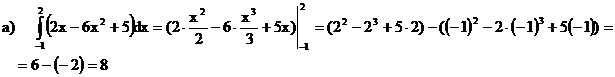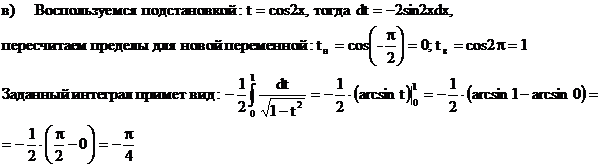Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Общая схема исследования функции и построения ее графика1. Найти область определения функции. Выделить особые точки (точки разрыва). 2. Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения. 3. Найти точки пересечения с осями координат 4. Установить, является ли функция чётной или нечётной. 5. Определить, является ли функция периодической или нет (только для тригонометрических функций, остальные непериодические, пункт пропускается). 6. Найти точки экстремума и интервалы монотонности (возрастания и убывания) функции. 7. Найти точки перегиба и интервалы выпуклости-вогнутости. 8. Найти наклонные асимптоты функции. 9. Построить график функции. Пример: Исследовать функцию методами дифференциального исчисления и построить график y = x3+6x2+9x+2 РЕШЕНИЕ: 1) Область определения функции – вся числовая прямая, то есть D (y) = (−∞; +∞) . Точек разрыва нет, вертикальных асимптот нет. 2) Точки пересечения с осями координат: Ox : найти затруднительно Oy:x=0⇒ 03 +6*02 +9*0+2=2 ⇒ Точка (0;2) 3)Функция общего вида, так как y(-x) = -x3 +6x2 -9x+2≠ ±y(x) 4) Экстремумы и монотонность. Вычисляем первую производную: y'=3x2 +12x+9 Находим критические точки: y'=0; 3x2 +12x+9=0; x1 =-1; x2 =-3. Исследуем знак производной на интервалах, на которые критические точки делят область определения функции. y' + - +
y -3 -1 x Функция возрастает на интервалах (−∞ ;-3),(-1; +∞) , убывает на интервале (-3;-1). Функция имеет минимум в точке x = -1 , y(-1) =-2 , функция имеет максимум в точке x = -3 , y(-3)=2. 5) Выпуклость и точки перегиба. Вычисляем вторую производную. y''=(3x2 +12x+9)'=6x+12  Находим критические точки: y''=0; 6x+12=0; x=-2. Исследуем знак производной на интервалах, на которые критические точки делят область определения функции. y'' - +
y -2 x Функция выпукла вверх на интервале (−∞;-2) , выпукла вниз на интервале (-2 ; +∞) . Точка перегиба: x =-2, y(-2) = 0. 6) Асимптоты. Так как 7) Строим график функции.
 
Интегральное исчисление.
Пример 2:
=
Пример 3:
Определенный интеграл. Если существует определенный интеграл от функции f(x) , то в этом случае функция называется интегрируемой на отрезке Для интегрируемости функции на отрезке Если функция непрерывна на
и имеет место формула
т.е. определенный интеграл от непрерывной функции равен разности значений первообразной функции (или неопределенного интеграла) при верхнем и нижнем пределах. Формула
называется формулой Ньютона-Лейбница. Пример 1: Необходимо найти определенный интеграл
Имеем:
Таким образом искомый интеграл равен 6. Пример 2: Вычислить интеграл: Решение:
- (
Примеры решения задач 1) Найти неопределенные интегралы:
Решение При решении примеров следует пользоваться свойствами неопределенных интегралов, таблицей интегралов, в которую включена формула интеграла функции линейного аргумента, непосредственным интегрированием и методом подстановки.
б) Выполнив почленное деление в подынтегральной функции, получим: в)
г) Будем использовать подстановку: д) Воспользуемся подстановкой:
2) Вычислить определенные интегралы:
Решение При вычислении определенных интегралов используем формулу Ньютона-Лейбница
3. Найти площадь фигуры, ограниченной линиями: у=1 – х2 + 4х и 2х – у – 2 =0 Для определения точек пересечения линий составим уравнение из равенства выражений этих линий: 1 – х2 + 4х = 2х – 2; получим уравнение: х2 – 2х – 3 = 0. Корнями этого уравнения являются числа: (-1) и 3. Для построения линий найдем значения функций и составим их таблицы:
Построив фигуру на плоскости, вычислим ее площадь, определив значение интеграла
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 259. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |





 =
=  =∞ , асимптот нет.
=∞ , асимптот нет. 
 то
то  где
где  – произвольная постоянная.
2.
– произвольная постоянная.
2.  где
где  – постоянная.
3.
– постоянная.
3. 

 .
2.
.
2.  3.
3.  .
4.
.
4.  5.
5.  6.
6.  7.
7.  8.
8.  9.
9.  10.
10.  11.
11.  12.
12. 


 -
-  +
+  )dx = 2
)dx = 2  dx -
dx - 
 dx -
dx - 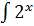 dx + 3
dx + 3  = 2
= 2  -
-  +3 arcsin x + C
При интегрировании использованы правила 2 и 3, а также табличные формулы 2,4,6,11.
+3 arcsin x + C
При интегрировании использованы правила 2 и 3, а также табличные формулы 2,4,6,11.
 где
где 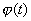 – монотонная, дифференцируемая функция; б)
– монотонная, дифференцируемая функция; б)  – новая переменная.
В первом случае формула замены переменной имеет вид:
– новая переменная.
В первом случае формула замены переменной имеет вид:
 . (1)
Во втором случае:
. (1)
Во втором случае:
 . (2)
В обоих случаях после интегрирования следует возвращаться к старой переменной обратной подстановкой.
Пример 1.
Вычислить интеграл:
. (2)
В обоих случаях после интегрирования следует возвращаться к старой переменной обратной подстановкой.
Пример 1.
Вычислить интеграл:
 Решение.
Сделаем замену переменных t=x+1 и найдем дифференциал от обеих частей, тогда
dt = (x+1)'dx ⇒ dt= dx
Подставляя все в исходный интеграл, получим:
Решение.
Сделаем замену переменных t=x+1 и найдем дифференциал от обеих частей, тогда
dt = (x+1)'dx ⇒ dt= dx
Подставляя все в исходный интеграл, получим:
 =
=  =
=  +C =
+C =  +C,
где C - const . Здесь заключительное действие - это обратная замена переменных.
В данном случае с помощью замены в интеграле удалось свести интеграл к табличному, затем была произведена обратная замена переменных и получен ответ.
+C,
где C - const . Здесь заключительное действие - это обратная замена переменных.
В данном случае с помощью замены в интеграле удалось свести интеграл к табличному, затем была произведена обратная замена переменных и получен ответ.
 (положим t = 2x+3, тогда x=
(положим t = 2x+3, тогда x=  t-
t-  , dx =
, dx =  =-
=-  +C= =-
+C= =- 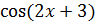 +C
+C  dx= (положим t= x2 +25, тогда dt = 2x dx, x dx=
dx= (положим t= x2 +25, тогда dt = 2x dx, x dx=  dt) =
dt) = 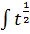 *
*  dt=
dt=  +C =
+C =  +C =
+C =  +C =
+C =  +C
+C .
. достаточно, чтобы она была непрерывна на нем или имела конечное число точек конечных разрывов.
достаточно, чтобы она была непрерывна на нем или имела конечное число точек конечных разрывов.


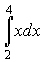


 =( 3
=( 3  + 4
+ 4  =
=  +2
+2  -
- +2
+2  26- 8=18.
26- 8=18.






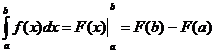 . Получение первообразной функции F(x) будем выполнять или непосредственно или способом подстановки.
. Получение первообразной функции F(x) будем выполнять или непосредственно или способом подстановки.