
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Расчет средней и предельной ошибки выборки.Расчет средней ошибки повторной простой случайной выборки производится следующим образом: - cредняя ошибка для средней
- cредняя ошибка для доли
Расчет средней ошибки бесповторной случайной выборки: - средняя ошибка для средней
- средняя ошибка для доли
Расчет предельной ошибки - предельная ошибка для средней
- предельная ошибка для доли
где t - коэффициент кратности; Расчет предельной ошибки бесповторной случайной выборки: - предельная ошибка для средней
- предельная ошибка для доли
Следует обратить внимание на то, что под знаком радикала в формулах при бесповторном отборе появляется множитель, где N - численность генеральной совокупности. Что касается расчета ошибки выборки в других видах выборочного отбора (например, типической и серийной), то необходимо отметить следующее. Определение необходимого объема выборочной совокупности. Когда исследователь приступает к эксперименту, возникает вопрос, какое количество объектов необходимо взять или сколько анализов нужно сделать, чтобы получить достоверные результаты. Другими словами, необходимо определить объем выборки или число n, от которого, как мы уже знаем, зависит величина ошибки репрезентативности, а значит и достоверность. Для этого используется формула:
t - критерий Стьюдента (мы задаем его сами, исходя из желаемой вероятности, чаще всего 2). Сигму (σ) можно предположить из исследований, проводимых ранее, или на других объектах, или вычислить ее примерное значение по формуле:
На величину Δ (дельта) отличаются генеральные данные от выборочных. Например, для средней арифметической: 
t * m = Δ, то есть погрешность. Чтобы установить необходимый объем выборки следует учесть несколько факторов. Один из наиболее важных – гомогенность – степень близости друг к другу членов данной совокупности с точки зрения изучаемых нами характеристик. Если каждый индивидуум в совокупности в точности такой же, как все остальные, то, выбрав всего лишь одного из них, мы получим действительно репрезентативную выборку. Напротив, если каждый индивидуум в совокупности абсолютно не похож ни на какой другой, то, прежде чем мы сможем утверждать, что у нас имеется репрезентативная выборка, нам потребуется провести перепись всей совокупности. В первом случае совокупность называют полностью гомогенной, во втором–полностью гетерогенной. Разумеется, в действительности большинство совокупностей располагается между этими двумя полюсами. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 523. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |




 повторной случайной выборки:
повторной случайной выборки:


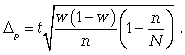
 , где
, где .
. , где
, где