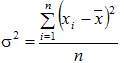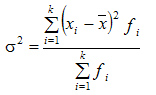Показатели размера интенсивности вариации: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсия, коэффициент вариации.

РАЗМАХ ВАРИАЦИИ - Мера разброса значений выборки наблюдений или распределения, рассчитываемая как разность между максимальным и минимальным значениями переменной.

Среднее линейное отклонение определяется как средняя арифметическая абсолютных значений отклонений отдельных вариантов от их средних арифметических.

1. Для первичного ряда:

2. Для вариационного ряда:

где сумма n — сумма частот вариационного ряда.

Среднее квадратичное отклонение определяется как обобщающая характеристика размеров вариации признака в совокупности. Оно равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической т.е. корень из дисперсии и может быть найдена так:

1. Для первичного ряда:

2. Для вариационного ряда:

Преобразование формулы среднего квадратичного отклонения приводит ее к виду, более удобному для практических расчетов:

Дисперсия или вариация ряда наблюдений зависит от отклонений или девиации одних элементов от других.

Дисперсия - представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины.

Дисперсия простая:

Дисперсия взвешенная:

Более удобно вычислять дисперсию по формуле:

Коэффициент вариации случайной величины — мера относительного разброса случайной величины; показывает, какую долю среднего значения этой величины составляет ее средний разброс. В отличие от среднего квадратического или стандартного отклонения измеряет не абсолютную, а относительную меру разброса значений признака в статистической совокупности. Исчисляется в процентах. Вычисляется только для количественных данных.