
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Аналитические решения заданного уравненияДано у'' – 3у' + 2у =х, у(0) = у'(0) = 1. (***)
Это линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами. Найдем общее решение уон этого уравнения, которое равно сумме какого-либо частного решения учн неоднородного уравнения и общего решения у∞ соответствующего однородного уравнения
уон = у∞ + учн.
Запишем соответствующее однородное уравнение
у'' – 3у' + 2у = 0,
его характеристическое уравнение k2 – 3k + 2 = 0 имеет корни k1 = 2, k2 = 1. Поэтому у∞ = с1е2х + с2е2х.
Для определения частного решения неоднородного уравнения (***) воспользуемся методом неопределенных коэффициентов. Так как правая часть уравнения (***) является многочленом первой степени и число ά + βi = 0 не является корнем характеристического уравнения, то частное решение имеет вид: учн =Ах +В. Чтобы определить значения коэффициентов А и В, находим производные
учн = А, учн = 0,
подставляем учн, учн, учн в уравнение (19)
-3А +2Ах + 2В = х
и, сравнивая коэффициенты при одинаковых степенях х, получаем систему
из которой находим
Найдем частное решение, удовлетворяющее заданным начальным условиям, для чего продифференцируем общее решение и подставим начальные условия в общее решение и его производную, в результате получим систему
решая которую, найдем
3. Сравним значения точного и приближенного решений заданного уравнения в точках х1, х2, х3. Это сравнение дано в табл.12.  Таблица 12
ПРИМЕРЫ ЗАДАНИЙ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Задание 1 Решить приближенно методом итерации и методом Зейделя. Сравнить ответы. Варианты задания:
Примечание. Для лучшей сходимости итерационного процесса необходимо преобразовать уравнения, выделив наибольшие диагональные элементы при неизвестных. Для этого необходимо или переобозначить неизвестные (циклическая перестановка) или переставить уравнения.
Задание 2 Решить систему линейных уравнений Варианты задания:
Задание 3 Найти все действительные корни уравнения
Варианты задания:
Задание 4 Построить кубическую сплайн-функцию для функции Варианты задания:
Задание 5
Вычислить приближенно
Варианты задания
Задание 6 Численно решить дифференциальное уравнение у' = f (x,y) с начальным условием у0 = у(х0) на отрезке [x0, b] с шагом h = 0,2 методом Эйлера, модифицированным методом Эйлера и методом Рунге-Кутта. Найти аналитическое решение у = у(х) заданного уравнения и сравнить значения точного и приближенных решений в точке x = b. Вычислить абсолютную и относительную погрешности в этой точке для каждого метода. Вычисления вести с четырьмя десятичными знаками.
Варианты задания
Задание 7 Методом Рунге-Кутта найти с точностью до ε = 10-3 решение дифференциального уравнения у = f (x,y) с начальным условием у(0) = 0 на отрезке [0;0,2]. Варианты задания
Задание 8 Методом Рунге-Кутта найти решение дифференциального уравнения y'' = f(x, y, z) c начальными условиями у(х0) = у0, Варианты задания |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 238. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 . Следовательно,
. Следовательно, 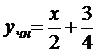 и
и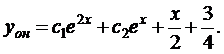


 .Таким образом, получили аналитическое решение заданного уравнения, удовлетворяющего данным начальным условиям
.Таким образом, получили аналитическое решение заданного уравнения, удовлетворяющего данным начальным условиям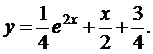
 - абсолютная погрешность
- абсолютная погрешность

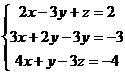
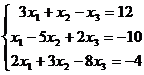











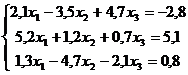




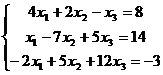





 , заданную в матричной форме, методом итерации, предварительно найдя значения неизвестных одним из прямых методов.
, заданную в матричной форме, методом итерации, предварительно найдя значения неизвестных одним из прямых методов.





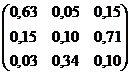
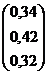
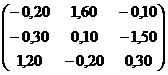























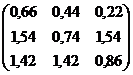







 с точностью
с точностью  комбинированным методом и методом итерации. Сравнить число шагов, необходимое для достижения одинаковой точности этими методами. Вычисления вести с одним запасным знаком.
комбинированным методом и методом итерации. Сравнить число шагов, необходимое для достижения одинаковой точности этими методами. Вычисления вести с одним запасным знаком.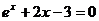


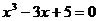




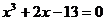









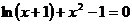




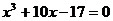



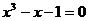


 , заданной таблично на отрезке
, заданной таблично на отрезке  .
.

 с точностью ε = 10-3, воспользовавшись той из формул приближенного интегрирования, которая потребует меньшего объема вычислений. Вычислить определенный интеграл точно и сравнить с приближенным его значением.
с точностью ε = 10-3, воспользовавшись той из формул приближенного интегрирования, которая потребует меньшего объема вычислений. Вычислить определенный интеграл точно и сравнить с приближенным его значением.















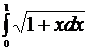


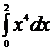





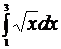

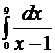



 [1,2]
[1,2]

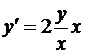












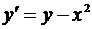















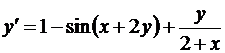









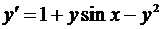


















 на отрезке [0;0,3] и с шагом h = 0,1. Найти аналитическое решение у(х) = у заданного уравнения и составить таблицу точного и приближенного решений заданного уравнения во всех точках х1, х2, х3. Все вычисления вести с шестью десятичными знаками.
на отрезке [0;0,3] и с шагом h = 0,1. Найти аналитическое решение у(х) = у заданного уравнения и составить таблицу точного и приближенного решений заданного уравнения во всех точках х1, х2, х3. Все вычисления вести с шестью десятичными знаками.