
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Аналитическое решение заданного уравненияУравнение у' – у = -2ху-1 есть уравнение Бернулли. Проинтегрируем его методом Бернулли, для чего положим у = uv, где u и v две неизвестные функции. Тогда исходное уравнение преобразуется к следующему:
u'v – v'u – uv = -2x(uv)-1
или u(v'–v)+ u'v = -2x(uv)-1 . (*)
Функцию v выберем из условия v' – v = 0, причем возьмем частное решение этого дифференциального уравнения v = ех. Подставив v в уравнение (*), получаем u' ех = -2хu-1е-х, а это – уравнение с разделяющими переменными. Решая его, находим u2 = с +2хе-2х + е-2х . Так как решение исходного уравнения есть произведения функций u и v, то получаем При начальном условии у(0) = 1 получим Таким образом, искомое частное решение имеет вид
Сравнение точного решения и приближенных решений исходного дифференциального уравнения Таблица 6
Контрольная работа №7 Пусть дано:
Для выбора шага интегрирования вычислим решение в точке х = 0,1 с шагом h = 0,1(табл.7) и с шагом h = 0,05 (табл.8). Таблица 7
В таблицах  Таблица 8
Так как полученные результаты совпадают в пределах заданной точности, вычисления продолжим с шагом h = 0,1 и с шагом h = 0,2. Результаты вычислений помещены в табл.9 и табл.10 соответственно.
Таблица 9
Таблица 10
Сравнение результатов расчета, полученных с шагом h = 0,1 и с шагом h = 0,2, показывает, что с точностью до ε = 10-3 можно принять у(0,2) ≈ 0,014158 и что в дальнейшем шаг расчета следовало бы снова удвоить.
Контрольная работа №8 Пусть дано:
Решение дифференциального уравнения методом Рунге-Кутта С помощью подстановки у' = z, у'' = z' заменим исходное дифференциальное уравнение системой уравнений: с начальными условиями у(0) = 1, z(0) = 1. Таким образом,
f1(x, y, z) = z, f2(x, y, z)= 3z –2y + x .
Шагом интегрирования h = 0,1 разобьем отрезок [0;0,3] на три равных части точками х0= 0, х1= 0,1, х2 = 0,2, х3 = 0,3. Для вычисления приближенных значений у1, у2, у3 и z1, z2, z3 решения системы (**) воспользуемся формулами (10.17). Результаты вычислений помещены в табл.11. Заполнение таблицы ведется в следующем порядке. При i = 0:
1. Записываем в первой строке х0 = 0, у0 = 1, z0 = 1. 2. Вычисляем f1(x0, y0, z0)= z0 = 1, f2(x0, y0, z0) = 3z0 –2y0 + x0 = 1, тогда К1(0) = 0,1∙1 = 0,1; l1(0) = 0,1∙1 = 0,1. 3. Записываем во второй строке
4. Вычисляем
тогда 5. Записываем в третьей строке
6. Вычисляем
тогда 7. Записываем в четвертой строке
8. Вычисляем
тогда 9. В столбцы 10. Вычислим
11. Получаем Значения
Таблица 11
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 219. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 .
.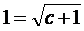 .
. .
. ; у(0) = 0; x
; у(0) = 0; x  [0,0,2];
[0,0,2];  .
. .
. ; у(0) = у'(0) = 1; [0;0,3]; h = 0,1.
; у(0) = у'(0) = 1; [0;0,3]; h = 0,1. (**)
(**)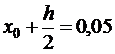 ,
,  ,
,  .
.


 .
.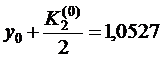 ,
,  .
.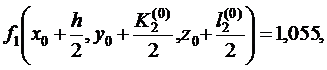
 ,
,
 .
. ,
,  ,
, 

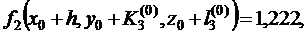

 .
.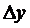 и
и 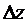 записываем числа K1(0), 2K2(0), 2K3(0), K4(0) и
записываем числа K1(0), 2K2(0), 2K3(0), K4(0) и  соответственно.
соответственно.
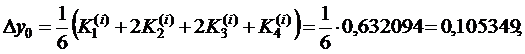



 заносим в строку, помеченную индексом i = 1, и снова проводим вычисления по формулам (10.17). В результате этих вычислений получаем следующую таблицу приближенных значений решения системы (**).
заносим в строку, помеченную индексом i = 1, и снова проводим вычисления по формулам (10.17). В результате этих вычислений получаем следующую таблицу приближенных значений решения системы (**).