
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Определение требуемой точности измерений.Многократное измерение одной и той же величины постоянного размера позволяют обеспечить требуемую точность. Поскольку ширина доверительного интервала зависит от количества экспериментов, то увеличивая n можно добиться выполнения наперед заданного условия Пример Имеется 10 независимых значений результата измерения линейного размера. Определить длину с вероятностью 0,95. Точность измерения не ниже
Решение 1.Используя вспомогательные вычисления получим: 2.Больше чем на 3 3.Допустим есть основание полагать, что измерения подчиняются нормальному закону. 4.Стандартное отклонение среднего арифметического равно 5.При 6.Так как 7.Пусть 8.Для проверки нормальности закона распределения используем составной критерий: при 9.Стандартное отклонение среднего арифметического 10. При На практике беспредельно повышать точность т.о. нельзя, т.к. рано или поздно определяющим становится не рассеяние расчета, а недостаток информации о поправках. Следовательно точность многократных измерений ограничивается дефицитом информации.  Многократное измерение с неравноточными значениями отсчета. При многократном измерении с неравными значениями отсчета, подчиняющегося нормальному закону, функция правдоподобия может быть представлена в виде
где все значения отсчета, полученные например, с помощью разных средств измерения, являются независимыми. Для оценки среднего значения результата измерения прологарифмируем эту функцию и, выполнив математические преобразование получим:
Это так называемое среднее взвешенное. В числителе отдельные значения результата измерения суммируются с «весами», обратно пропорциям их дисперсиям. Тем самым, более точным значениям придается больший вес. Наличием суммы в знаменателе обеспечивается то, что в выражении
Сумма всех весов равна единице: Математическое ожидание среднего взвешенного |
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 337. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
. =2см.
=2см.



 =392,
=392,  =2,5
=2,5
 Р=0,95 по графику распределения Стьюдента находим t=2,3.
Р=0,95 по графику распределения Стьюдента находим t=2,3. , то необходимо увеличить количество экспериментальных данных.
, то необходимо увеличить количество экспериментальных данных.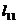 =390, следовательно
=390, следовательно 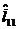 =391,8 и
=391,8 и  и ни одно из численных значений
и ни одно из численных значений 

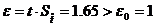 , следовательно необходимо увеличивать количество экспериментальных данных. При таком задании
, следовательно необходимо увеличивать количество экспериментальных данных. При таком задании 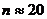 .
.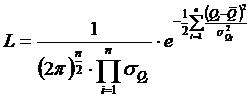


 , где нормированный вес каждого значения равен
, где нормированный вес каждого значения равен  .
. . Т.о. среднее взвешенное является несмещенной оценкой среднего значения результата измерения.
. Т.о. среднее взвешенное является несмещенной оценкой среднего значения результата измерения.