
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Вопрос №24-30. Постановка и решение задачи максимизации прибыли фирмы с производственной функцией Кобба – Дугласа при отсутствии каких-либо ограничений по её деятельности.Задача максимизации прибыли фирмы имеет вид х1,х2– переменные,
Условия первого порядка для нее таковы:
Это те же самые условия, что и условия равенства стоимости предельного продукта фактора цене этого фактора, приведенные в тексте. Посмотрим, как выглядит поведение фирмы, максимизирующее прибыль, в случае производственной функции Кобба-Дугласа. Предположим, что функция Кобба-Дугласа задана в виде
Решая систему, получаем
это выражения для спроса на два фактора производства как функции выбора оптимального выпуска. Далее надо найти выражение для оптимального выбора объема выпуска. Подставляя выражения для оптимального спроса на факторы в производственную функцию Кобба-Дугласа, получаем выражение
Вынеся уза скобки в левой части уравнения, получаем
или
Это выражение для функции предложения фирмы с производственной функцией Кобба-Дугласа. Наряду с выведенными выше функциями спроса на факторы Модель Леонтьева многоотраслевой экономики Балансовые соотношения Модель Леонтьева — это статическая модель линейной многоотраслевой экономики. В её основе лежат следующие предположения. 1. В экономической системе производятся, продаются, покупаются, потребляются и инвестируются п продуктов. 2. Каждая отрасль хозяйства является «чистой», то есть производит только один продукт. Разные отрасли производят разные продукты. 3. Под производственным процессом в каждой отрасли понимается преобразование типов ресурсов в определённый продукт. При этом соотношение затраченных продуктов предполагается постоянным. Это означает, что, если для производства единицы j-го продукта требуется затратить  Обозначим:
Так как валовый объём продукции любой i–й отрасли равен суммарному объёму продукции, потребляемой п отраслями и конечного продукта, то
Уравнения (52) называются соотношениями баланса:
Так как продукция разных отраслей имеет разные измерения, то в дальнейшем будем иметь в виду стоимостный баланс. В стоимостном межотраслевом балансе все величины, входящие в (52), имеют стоимостное выражение. Дополнение к вопросам 24-30. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 571. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
.
 . Тогда указанные два условия первого порядка принимают вид:
. Тогда указанные два условия первого порядка принимают вид:
 ,
, 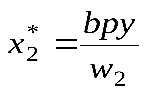 ,
, .
. ,
, .
. и
и  оно дает нам полное решение задачи максимизации прибыли.
оно дает нам полное решение задачи максимизации прибыли. единиц i –го ресурса, то для выпуска l единиц j-го продукта следует затратить уже
единиц i –го ресурса, то для выпуска l единиц j-го продукта следует затратить уже  единиц i–го ресурса. Значит, независимо от масштаба производства, удельный выпуск и соотношения затрат предполагаются постоянными. Часть продукции идёт на внутрипроизводственное потребление данной отраслью (данным предприятием) и другими отраслями, а другая часть предназначена для целей конечного (вне сферы материального производства) личного и общественного потребления.
единиц i–го ресурса. Значит, независимо от масштаба производства, удельный выпуск и соотношения затрат предполагаются постоянными. Часть продукции идёт на внутрипроизводственное потребление данной отраслью (данным предприятием) и другими отраслями, а другая часть предназначена для целей конечного (вне сферы материального производства) личного и общественного потребления. - общий валовый объём продукции i–й отрасли,
- общий валовый объём продукции i–й отрасли, 
 - объём продукции i–йотрасли, потребляемый j–й отраслью в процессе производства при выпуске объёма продукции
- объём продукции i–йотрасли, потребляемый j–й отраслью в процессе производства при выпуске объёма продукции 
 -объём конечного продукта i–й отрасли для непроизводственного потребления,
-объём конечного продукта i–й отрасли для непроизводственного потребления,  .
. ,
,  . (52)
. (52)