
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Вопрос №21. Средние и предельные характеристики производственной функции Кобба – Дугласа. Эластичность выпуска продукции. (См. вопрос №20).1. Эластичность выпуска продукции. Параметры a и b являются коэффициентами частной эластичности объема производства Y по затратам капитала K и труда L соответственно:
Они показывают, на сколько процентов в среднем изменится Y, если K и L увеличить соответственно на один процент: увеличение затрат капитала на 1% приведет к росту выпуска продукции на a %, а увеличение затрат труда на 1% приведет к росту выпуска на b %. 2. Эффект от масштаба производства. При росте затрат каждого из факторов K и L в l раз выпуск продукции возрастет в la +bраз. Это означает следующее: · если a + b> 1, то функция Кобба-Дугласа имеет возрастающую отдачу от масштаба производства; · если a + b< 1, то функция Кобба-Дугласа имеет убывающую отдачу от масштаба производства; · если a + b = 1, то функция Кобба-Дугласа имеет постоянную отдачу от масштаба производства. 3. Прогнозируемые доли производственных факторов. В рыночной экономике оценки a и b интерпретируются как прогнозируемые доли дохода, полученные соответственно за счет капитала и труда. Учитывая влияние случайных возмущений, присущих каждому экономическому явлению, функцию Кобба-Дугласа можно представить в виде
Полученную степенную (мультипликативную) модель легко свести к линейной путем логарифмирования обеих частей уравнения:
Введя новые переменные и параметры
получим модель множественной линейной (относительно преобразованных переменных и параметров) регрессии
Предположим, что в модели a + b = 1. Это условие означает, что при расширении масштаба производства – увеличении затрат капитала K и труда L в некоторое число раз – объем производства возрастет в то же число раз. Тогда функцию Кобба-Дугласа можно представить в виде 
или
Таким образом, получаем зависимость производительности труда (Y/L) от капиталовооруженности (K/L). Для оценки параметров модели путем логарифмирования приводим ее к модели парной линейной регрессии:
Функция Кобба-Дугласа с учетом технического прогресса имеет вид:
где t – время; параметр q – темп прироста объема производства благодаря техническому прогрессу. Модель (4.13) приводится к линейному виду аналогично модели. Пример.По данным 50 предприятий легкой промышленности получена оценка производственной функции Кобба-Дугласа в следующем виде:
или
Коэффициент регрессии, равный 0,25, который одновременно является коэффициентом эластичности, показывает, что при изменении капиталовооруженности труда на 1% производительность труда на предприятиях отрасли увеличивается в среднем на 0,25%. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 494. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 .
. .
. ,
, .
. ,
, . (4.11)
. (4.11) .
.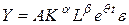 ,
, ,
, .
.