
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Решение нелинейного уравнения методом НьютонаРассмотрим применение метода Ньютона сначала для решения одного нелинейного уравнения f(х)=0, где f(х) - непрерывно дифференцируемая функция. Функцию f(х) можно разложить в ряд Тейлора в окрестностях произвольно взятой точки х(0)
Если в многочлене (1) отбросить производные высших порядков и оставить только линейные члены, то получим
где Эта операция называется линеаризацией нелинейного уравнения. Из линеаризованного уравнения (2) можно выразить поправку
и вычислить новое (первое) приближение к корню
Если подставить значение Таким образом, суть метода Ньютона заключается в линеаризации нелинейного уравнения и решении полученного линейного уравнения на каждой итерации. Значение корня линейного уравнения является очередным приближением к корню решаемого нелинейного уравнения. Графическая иллюстрация применения метода Ньютона для решения нелинейного уравнения f(х)=0 дана на рисунке.
Как видно из рисунка, к действительному корню  Алгоритм решения нелинейного уравнения f(х)=0 методом Ньютона состоит из следующих действий: 1. Задаем начальное приближение х(0). 2. Вычисляем невязку f(х(0)). 3. Определяем 4. Вычисляем поправку ∆х(1) (как катет АС прямоугольного треугольника АВС).
5.
6. Вычисляем невязку f(х(1)) и проверяем условие Если условие выполняется, то вычислительный процесс заканчивается, в противном случае повторяем действия начиная с 3-го. Примечание: 1. Значение ε задается в каждом конкретном случае и не должно быть равным нулю, так как итерационный метод не позволяет определить абсолютно точное значение корня (это обычно практически не требуется). Неоправданное снижение значения ε не рекомендуется, поскольку при этом увеличивается число итераций. 2. Если у функции f(х)=0 имеется несколько корней, то метод Ньютона позволяет найти вещественный корень и причем только один в области притяжения которого находится начальное приближение.
Пример: нужно решить нелинейное уравнение 7х3+5х-1=0 (ε = 0,01)
2. |f(х(0))=1|>ε | Начальная невязка f(х(0))=1| ≥ε
2. 3. х(1)=х(0)-∆х(1)=0-(-0,2)=0,2 4. f(x(1))=7∙0,23+5∙0,2-1=0,056 |0,056| > ε
2. 3. х(2)=х(1)-∆х(2)=0,2-0,01=0,19 4. f(x(2))=7∙0,193+5∙0,19-1=0,048+0,95-1=0,002 |0,002|< ε Результаты расчетов целесообразно представить в следующей таблице
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 496. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
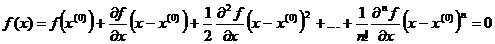 . (1)
. (1)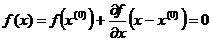 , (2)
, (2)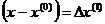 - называется поправкой.
- называется поправкой.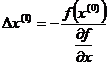 (3)
(3)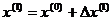 . (4)
. (4)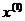 в f(х), то получим невязку
в f(х), то получим невязку 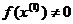 . По величине невязки
. По величине невязки 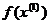 можно судить о близости
можно судить о близости 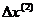 , подставляя в линеаризованное уравнение (2) значение
, подставляя в линеаризованное уравнение (2) значение 
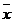 нелинейного уравнения приближаемся последовательно от заданного начального приближения х(0).
нелинейного уравнения приближаемся последовательно от заданного начального приближения х(0).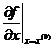 - значение производной (как тангенс угла
- значение производной (как тангенс угла 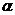 , образованного касательной к кривой в точке В с осью х).
, образованного касательной к кривой в точке В с осью х).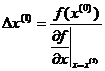 .
.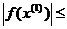 ε.
ε.
 0 итерация 1. х(0)=0 Зададим х(0)=0
0 итерация 1. х(0)=0 Зададим х(0)=0 1 итерация 1.
1 итерация 1. 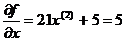
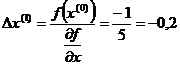
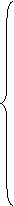 2 итерация 1.
2 итерация 1. 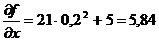
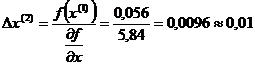
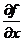 тангенс
тангенс