
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Третий способ вычисления определителя
Самый лучший способ вычисления определителя для матриц большой размерности и если элементы являются нецелыми числами, заключается в преобразовании данной квадратной матрицы к треугольному виду, т.е. к такому виду, когда у полученной после преобразования матрицы все элементы сверху или снизу главной диагонали являются нулевыми
Определитель искомой квадратной матрицы А равен произведению диагональных элементов полученной треугольной матрицы Преобразование квадратной матрицы к треугольному виду рассмотрим позднее («прямой ход» методом Гаусса).
Действия с матрицами
1. Сумма и разность матриц. Могут складываться и вычитаться матрицы только одинакового типа.
Из сложения матриц вытекают следующие свойства:
1) А+(В+С)=(А+В)+С; 2) А+В=В+А; 3) А+0=А.
2. Умножение матрицы на скаляр. Отсюда: 1) 1А=А; 2) 0А=0; 3) α (β А) = (αβ) А; 4) αА + βА = (α+β) А; 5) α (А+В) = αА + αА;
3. Умножение матриц А * В = С.
Перемножать матрицы можно только в том случае, если число столбцов первой матрицы равно числу строк второй матрицы, т.е. g=p, а число строк первой матрицы и число столбцов второй матрицы могут быть любые, т.е. m≠n. Результатом будет матрица С размерностью mn, элементы которой
Для вычисления элемента, стоящего в i-й строке и j-м столбце произведения двух матриц, нужно элементы i-ой строки первой матрицы умножить на соответствующие элементы j-го столбца второй матрицы и полученные произведения сложить.  Свойства: 1) А(ВС)=(АВ)С; 2) α(АВ)=(αА)В; 3) (А+В)=АС+АВ. 4) Запомнить, что в общем случае 4) АВ≠ВА. Пример:
В тех частных случаях, когда АВ=ВА, матрицы А и В называются перестановочными. Например, единичная матрица Е перестановочна с любой матрицей А того же порядка. АЕ=ЕА=А. Единичная матрица Е играет роль единицы при умножении.
Транспонированная матрица Если в матрице Свойства: 1) дважды транспонированная матрица равна исходной А = (А ) = А; 2) (А+В) =А + В ; 3) (АВ) =В А , т.е. (АВ) ≠ А В ; 4) Если А =А, то матрица А - симметричная (аij = aji)
Обратная матрица
Обратной матрицей по отношению к данной квадратной, называется матрица, которая, будучи умноженной как справа, так и слева на данную матрицу, дает единичную матрицу. Обозначим для матрица А обратную ей матрицу через А-1. АА-1=А-1А=Е. Нахождение обратной матрицы для данной называется обращением данной матрицы. Квадратная матрица называется неособенной, если ее определитель не равен нулю, в противном случае матрица называется особенной или сингулярной. Обратная матрица имеет только у неособенной матрицы. Пусть имеем матричное равенство АС=В. Умножим правую и левую часть равенства на обратную матрицу А-1 А-1АС= А-1В. Поскольку известно, что А-1А=Е, то ЕС= А-1В. И поскольку известно, что ЕС=С, то С= А-1В. То есть, мы равенство АС=В преобразовали в равенство С= А-1В, выразив матрицу С. Если бы у нас были простые алгебраические числа а, b и с, то аналогичные преобразования были бы следующие: Сравнив преобразования для алгебраических чисел и матриц видим, что обращение матрицы соответствует действию деления. Поэтому понятна необходимость в обратной матрице, в ее вычислениях.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 483. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
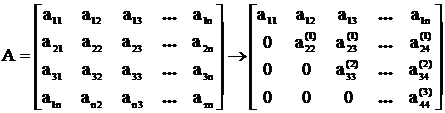 .
.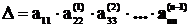 .
.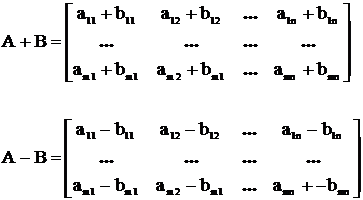
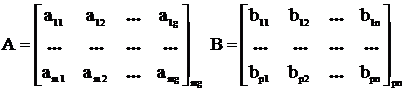
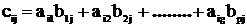
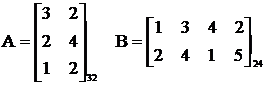
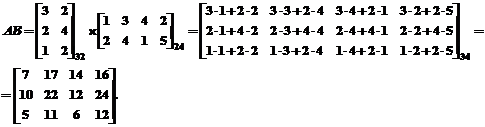
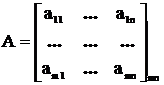 строки и столбцы поменять местами, то получим транспонированную матрицу.
строки и столбцы поменять местами, то получим транспонированную матрицу.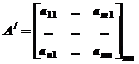
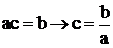 .
.