Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Линейные дифференциальные уравнения ⇐ ПредыдущаяСтр 5 из 5 1. ЛОДУ 2П с постоянными коэффициентами 2. ЛОДУ n-го порядка с постоянными коэффициентами 3. Линейные неоднородные ДУ, структура общего решения 4. ЛНДУ 2П с постоянными коэффициентами и специальной правой частью 5. Метод вариации произвольных постоянных Цель занятия: Изучить понятие неоднородного дифференциального уравнения, научиться решать линейные дифференциальные уравнения. Роль и место лекции В предыдущей лекции были представлены методы понижения порядка ДУ, а так же структура общего решения линейного однородного (без правой части) ДУ второго порядка. Однако не были рассмотрены методы получения линейно независимых решений, а так же не была рассмотрена структура общего решения линейного неоднородного (с правой частью) ДУ. Этим вопросам будет посвящена данная лекция. Представленный материал, прежде всего, необходим при изучении темы «Системы ДУ» и «Элементы теории поля». Кроме того, подобные типы ДУ наиболее часто встречаются при решении прикладных задач. Таких, например как вопросы роста популяции, распространения эпидемии, рационального хозяйствования ресурсов и др. Вопрос № 1. ЛОДУ 2П с постоянными коэффициентами Частным случаем линейного однородного ДУ 2-го порядка является ЛОДУ 2-го порядка с постоянными коэффициентами
где p и q – постоянные величины. Найдем решение ДУ (1) в виде где k такое, что выражение (2) удовлетворяет уравнению (1). Подставим  Определение № 1. Квадратное уравнение Правило!!! Чтобы составить характеристическое уравнение данного ДУ надо заменить Построение общего решения (1) зависит от корней характеристического уравнения. 1.1. Случай Пусть корни характеристического уравнения (3) действительны и различны
1.2. Случай Пусть корни характеристического уравнения (3) действительны и равны 1.3. Случай корни комплексные (сопряженные) Пусть
1.4. Таблица решений ЛОДУ 2П Таблица 1.
Вопрос № 2. ЛОДУ n-го порядка с постоянными коэффициентами Определение № 2. Линейным однородным ДУ n-го порядка с постоянными коэффициентами называется уравнение вида Обобщая проведенные ранее рассуждения, запишем характеристическое уравнение для такого ДУ в виде Определение № 3 Количество равных корней между собой называются кратностью одного корня. Так уравнение Вывод!!! Таким образом, можно сделать вывод, что общее решение ЛОДУ n-го порядка с постоянными коэффициентами состоит из функций Вопрос № 3. Линейные неоднородные ДУ, структура общего решения Аналогично ЛОДУ линейные неоднородные дифференциальные уравнения ЛНДУ имеют структуру общего решения. Запишем ЛНДУ 2-го порядка в виде
или в кратком виде Теорема № 1 (о структуре общего решения ЛНДУ 2П). Общее решение линейного неоднородного дифференциального уравнения второго порядка имеет вид Доказательство. Покажем, что 4. ЛНДУ 2П с постоянными коэффициентами и специальной правой В предыдущих вопросах были рассмотрены методы определения общего решения ЛОДУ 2П Таблица 2.
Замечание!!! 1. Если правая часть имеет только 2. Неопределенными коэффициенты находят после подстановки частного решения в исходное ДУ. ПРИМЕР № 1. Найти общее решение ДУ ПРИМЕР № 2. Найти общее решение ДУ Частное решение исходного уравнения находим из таблицы Теорема № 2. Частное решение ЛНДУ 2П вида Пример № 3. Найти общее решение ЛНДУ Правая часть ЛНДУ можно представить в виде Вопрос № 5. Метод вариации произвольных постоянных В случае если ЛНДУ 2П имеет общий вид Заключение В заключении отметим, что отсутствие в однородном ДУ правой части, обусловлено свойством однородности функции (см. Л. 51). Данная лекция была посвящена вопросам решения линейных однородных ДУ второго порядка, однако приведенные рассуждения можно обобщить на случай ДУ n-го порядка по аналогии с решением систем уравнений с n-уравнениями. Так общим решение ЛОДУ n-го порядка будет - в силу линейного построения ДУ его общее решение так же является линейной комбинацией частных линейно независимых решений, то есть составляют фундаментальную систему; - только неполные ДУ высших порядков допускают снижение порядка; - при снижении порядка используют подстановку - общее решение ЛОДУ 2П состоит из двух линейно независимых решений; - в линейном однородном ДУ нет правой части Литература 24. Баврин И.И. Высшая математика. – М.: Просвещение, 2003. – 384 с. 25. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. – Ростов-на-Дону: Феникс, 1997. – 512 с. 26. Демидович Б.П., Кудрявцев В.А.Краткий курс высшей математики. – М.: Астрель, 2001. - 656 с. Лекция № 55 Линейные операторы 1. Операторы в 2. Дифференциальные и интегральные операторы 3. Операторные уравнения Цель занятия: Изучить понятие оператора, научиться применять линейные операторы в решении операторных уравнений. Роль и место лекции Теория операторного исчисления является необходимой составляющей в решении сложных задач математического моделирования, связанных с преобразованием пространств. Операторное преобразование позволяет облегчить восприятие сложных расчетов преобразования и упростить их анализ.
Вопрос № 1. Понятие оператора в пространстве 1.1. Понятие оператора Пусть даны линейные векторные пространства Определение № 1. Оператором
Вектор Совокупность всех элементов множества, для которых определен оператор, называется областью определения оператора. Определение № 2 Линейным оператором называется оператор 1. 2. Следствие!!!
Т. е. линейную комбинацию векторов линейный оператор переводит в такую же линейную комбинацию их образов. Если пространства совпадают ( ПРИМЕР № 1. 1. Единичный оператор 2. Нулевой оператор 3. Оператор подобия 1.2. Оператор в пространстве Пусть задан базис пространства
т. е. для
где
откуда, согласно определению № 2, в силу линейности оператора получим
Для базиса (1) линейное преобразование
Сравнивая выражения (3) и (5) на основании единственности разложения вектора в данном базисе, заключаем
Выпишем матрицу коэффициентов системы линейных уравнений
Матрица (6) называется матрицей линейного оператора. Она однозначно определяется для оператора Вывод!!! Линейный оператор в
Вопрос № 2. Дифференциальные и интегральные операторы 2.1. Дифференциальный оператор Рассмотрим На
где 2.2. Интегральный оператор В
где Вопрос № 3. Операторные уравнения Запишем
Решение Определение № 3. Значения Определение № 4. Ненулевые векторы Теорема № 1. Если Доказательство. Пусть Следствие!!! Собственный вектор модно искать с точностью до числового множителя. Т. е. оператор задает направление. Чаще за собственный вектор принимают нормированный вектор Определение № 5. Совокупность всех собственных чисел оператора называется спектром оператора в Рассмотрим спектр
соответствующее системе линейных уравнений
Система линейных однородных уравнений совместна, т. к.
Правило нахождения спектра оператора 1. Находим 2. Для каждого ПРИМЕР №2. Пусть задан линейный оператор
Заключение Материал данной лекции будет необходим при изучении следующей лекции «Квадратичные формы». Важно понимание смысла оператора, действующего в пространстве как аппарата преобразующего это пространство. Важно различать смысл понятий оператора, функционала и функции. Отметим наиболее важное: - оператор преобразует пространство (существуют образы и прообразы). - оператор может быть линейным. - существует матрица линейного оператора. - существуют интегральный и дифференциальный операторы. - собственные числа оператора образуют его спектр. - собственные вектора, соответствующие спектру оператора являются решением операторного уравнения. - при нахождении собственных чисел линейного оператора в пространстве Литература 27. Ильин В.А., Позняк Э.Г. «Линейная алгебра». – М.: Физматлит, 2001. – 320 с. 28. Садовничий В. А. Теория операторов. – М. Дрофа, 2001. – 384 с. 29. Демидович Б.П., Кудрявцев В.А. Краткий курс высшей математики. – М.: Астрель, 2001. - 656 с.
Лекция № 56 Квадратичные формы 1. Самосопряженные операторы. 2. Квадратичные формы 3. Приведение уравнения кривых второго порядка к каноническому виду Цель занятия: Изучить понятие квадратичной формы, научиться приводить уравнения кривых второго порядка к каноническому виду. Роль и место лекции Применение теории операторного исчисления позволяет исследовать уравнения второго порядка как результат преобразования пространства. Так в результате воздействия линейного оператора кривые второго порядка меняют направление основных асимптот, директрис и осей. Вопрос № 1. Самосопряженные операторы Пусть задано Евклидово пространство Определение № 1. Линейный оператор называется самосопряженным, если для любых Теорема № 1. Если Доказательство. Пусть
Из определения № 1 следует, что Вопрос № 2. Квадратичные формы Определение № 2. Квадратичной формой от «n» переменных называется однородный многочлен второй степени относительно этих переменных.
В частности от двух переменных
От трех переменных
Составим симметрическую матрицу из коэффициентов квадратичной формы. Коэффициенты при квадратах переменных запишем на главной диагонали, а остальные коэффициенты разделим на 2 и расположим симметрично относительно главной диагонали Определение № 3 Симметрическая матрица, составленная из коэффициентов квадратичной формы, называется матрицей этой формы. Так для
В пространстве Определение №4 Главными направлениями квадратичной формы называются направления собственных векторов этой формы. Теорема № 2. Квадратичная форма в Доказательство. Определим собственные числа матрицы квадратичной формы
1. 2. Матрица квадратичной формы Определение № 5 Квадратичная форма, содержащая только квадраты переменных, называется канонической
Теорема № 3. Если за базисные векторы принять собственные векторы (главные напрвлвения) матрицы квадратичной формы, то она принимает канонический вид. Доказательство. Дано
в новом базисе представим в виде
Сравнивая (3) и (4) получим систему преобразований
Подставим (5) в квадратичную форму
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 185. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , (1)
, (1)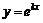 , (2)
, (2) и
и 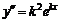 в (1) и получим
в (1) и получим  , откуда
, откуда (3).
(3). для определения коэффициента k функции
для определения коэффициента k функции  на
на  ,
,  на
на  и
и  на 1.
на 1.
 и
и  , поскольку
, поскольку 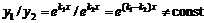 . По теореме о структуре общего решения (см. Л. 53) имеем
. По теореме о структуре общего решения (см. Л. 53) имеем . (4)
. (4)
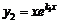 , тогда функции
, тогда функции  и
и  будут линейно независимые. Покажем, что
будут линейно независимые. Покажем, что  ,
,  в выражение (1). Получим
в выражение (1). Получим 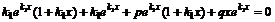 , сократим на
, сократим на 
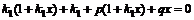 . Сгруппируем
. Сгруппируем  . Согласно (3)
. Согласно (3)  так как
так как  – единственный корень характеристического уравнения, тогда по теореме Виета
– единственный корень характеристического уравнения, тогда по теореме Виета 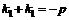 , откуда вторая часть равенства
, откуда вторая часть равенства 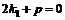 и функция
и функция  является решение (1). Тогда общее решение (1)
является решение (1). Тогда общее решение (1) . (5)
. (5)
 и
и 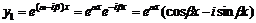 . На основании свойств ЛОДУ решения будут так же функции
. На основании свойств ЛОДУ решения будут так же функции 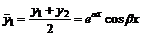 и
и 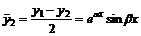 . Легко заметить, что эти функции линейно не зависимы, т. е.
. Легко заметить, что эти функции линейно не зависимы, т. е.  . Тогда общим решением ДУ (1) будет выражение
. Тогда общим решением ДУ (1) будет выражение . (6)
. (6)



 .
.  , которое имеет n корней
, которое имеет n корней  , среди которых могут быть равные между собой и комплексные.
, среди которых могут быть равные между собой и комплексные.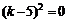 имеет два равных корня
имеет два равных корня  один корень
один корень 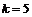 с кратностью
с кратностью 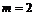 .
. , количество которых (i) равно числу корней с кратностью
, количество которых (i) равно числу корней с кратностью 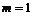 , из функций
, из функций  , количество которых (j) равно числу корней с кратностью
, количество которых (j) равно числу корней с кратностью  , из функций
, из функций  , количество которых (t) равно числу пар комплексных корней кратности
, количество которых (t) равно числу пар комплексных корней кратности  и из функций
и из функций  , количество которых (s) равно числу пар комплексных корней кратности
, количество которых (s) равно числу пар комплексных корней кратности  (7)
(7) .
. , где
, где  – общее решение, соответствующего линейного однородного ДУ
– общее решение, соответствующего линейного однородного ДУ  ,
,  – частное решение исходного уравнения.
– частное решение исходного уравнения. является решением (7). Для этого подставим его в (7). Получим
является решением (7). Для этого подставим его в (7). Получим 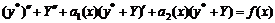 . Сгруппируем данное уравнение по функциям
. Сгруппируем данное уравнение по функциям 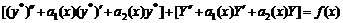 . По условию первое слагаемое
. По условию первое слагаемое 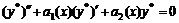 как общее решение ЛОДУ, второе слагаемое
как общее решение ЛОДУ, второе слагаемое  как частное решение ЛНДУ. Покажем, что это решение общее, то есть для любых начальных условий (НУ) при
как частное решение ЛНДУ. Покажем, что это решение общее, то есть для любых начальных условий (НУ) при  и
и  существуют единственные коэффициенты
существуют единственные коэффициенты  и
и  , такие, что
, такие, что 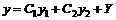 – есть решение уравнения (7). Для этого подставим НУ в (7) и получим систему уравнений
– есть решение уравнения (7). Для этого подставим НУ в (7) и получим систему уравнений  относительно
относительно  . Данная система из двух уравнений и двух неизвестных
. Данная система из двух уравнений и двух неизвестных  . Этот определитель есть Вронскиан двух функций
. Этот определитель есть Вронскиан двух функций 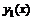 и
и  , которые линейно независимы по условию. Тогда
, которые линейно независимы по условию. Тогда  и система имеет единственное решение
и система имеет единственное решение  есть общее решение ЛНДУ 2П.
есть общее решение ЛНДУ 2П. . Для нахождения общего решения линейного неоднородного ДУ 2-го порядка необходимо, согласно теоремы 1, определить его частное решение. Порядок его получения аналогичен порядку, приведенному в предыдущих вопросах. Ниже представим таблицу № 1, позволяющую определить
. Для нахождения общего решения линейного неоднородного ДУ 2-го порядка необходимо, согласно теоремы 1, определить его частное решение. Порядок его получения аналогичен порядку, приведенному в предыдущих вопросах. Ниже представим таблицу № 1, позволяющую определить  .
.
 – многочлен степени n
– многочлен степени n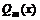 – многочлен степени m
– многочлен степени m – не корни характеристического уравнения
– не корни характеристического уравнения
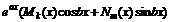

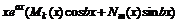
 и
и 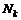 - многочлены с неопред. коэффициентами.
- многочлены с неопред. коэффициентами.
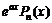
 ,
, 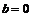
 – не корень характеристического уравнения
– не корень характеристического уравнения
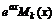


 ,
, 


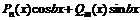

 – не корни характеристического уравнения
– не корни характеристического уравнения
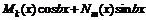

 или
или  , частное решение содержит обе функции.
, частное решение содержит обе функции. . Найдем общее решение ЛОДУ
. Найдем общее решение ЛОДУ 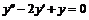 . Характеристическое уравнение
. Характеристическое уравнение 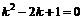 имеет корень
имеет корень  кратности 2. Следовательно
кратности 2. Следовательно  . Частное решение исходного уравнения находим из таблицы
. Частное решение исходного уравнения находим из таблицы  ,
,  и
и  , поэтому частным решением будет многочлен первой степени
, поэтому частным решением будет многочлен первой степени  , где A и B – неопределенные коэффициенты. Подставим это решение в исходное ДУ. Очевидно,
, где A и B – неопределенные коэффициенты. Подставим это решение в исходное ДУ. Очевидно,  ,
,  . Тогда
. Тогда  или
или  . С учетом равенства соответствующих коэффициентов многочленов запишем систему
. С учетом равенства соответствующих коэффициентов многочленов запишем систему 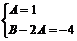 , откуда
, откуда  ,
,  . Поэтому частное решение данного уравнения имеет вид
. Поэтому частное решение данного уравнения имеет вид  , а общее решение имеет вид
, а общее решение имеет вид  .
.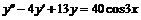 . Найдем общее решение ЛОДУ
. Найдем общее решение ЛОДУ 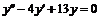 . Характеристическое уравнение
. Характеристическое уравнение  имеет комплексные корни
имеет комплексные корни 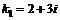 ,
,  . Следовательно, согласно таблице 1
. Следовательно, согласно таблице 1  =
=  .
.
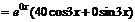 ,
,  , причем
, причем  не корни характеристического уравнения, поэтому частным решением будет
не корни характеристического уравнения, поэтому частным решением будет  . Здесь
. Здесь  и
и  ,
,  многочлены нулевой степени, а A и B – неопределенные коэффициенты. Подставим это решение в исходное ДУ. Очевидно,
многочлены нулевой степени, а A и B – неопределенные коэффициенты. Подставим это решение в исходное ДУ. Очевидно,  ,
,  . Тогда
. Тогда 
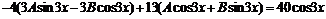 или
или  . С учетом равенства соответствующих коэффициентов многочленов запишем систему
. С учетом равенства соответствующих коэффициентов многочленов запишем систему  , откуда
, откуда 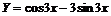 , а общее решение имеет вид
, а общее решение имеет вид  .
. имеет вид
имеет вид 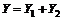 , где
, где  – частное решение ДУ
– частное решение ДУ 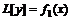 ,
,  – частное решение ДУ
– частное решение ДУ  .
.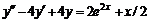 второго порядка. Общее решение имеет вид
второго порядка. Общее решение имеет вид  . Его характеристическое уравнение
. Его характеристическое уравнение  . Корень уравнения
. Корень уравнения  имеет кратность 2, поэтому (таблица № 1) общее решение этого ЛОДУ будет
имеет кратность 2, поэтому (таблица № 1) общее решение этого ЛОДУ будет  .
. , где
, где  и
и 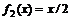 . Тогда частным решением ЛНДУ будет
. Тогда частным решением ЛНДУ будет  – частное решение ЛНДУ
– частное решение ЛНДУ  . Согласно таблице № 2 с учетом того, что
. Согласно таблице № 2 с учетом того, что  . Подставим данное решение в ДУ и получим
. Подставим данное решение в ДУ и получим  , сократив получим
, сократив получим  . Раскроим скобки и приведем подобные
. Раскроим скобки и приведем подобные  или
или  . Откуда
. Откуда  , а
, а  . Аналогично необходимо найти частное решение ЛНДУ
. Аналогично необходимо найти частное решение ЛНДУ  . Согласно таблице № 2 частное решение для
. Согласно таблице № 2 частное решение для  ,
,  , будет иметь вид
, будет иметь вид  . Тогда подстановка
. Тогда подстановка  ,
,  дает
дает  . Решая
. Решая  , составим систему
, составим систему  , откуда
, откуда  , Тогда общее решение ЛНДУ 2П будет
, Тогда общее решение ЛНДУ 2П будет  .
. , то для его решения применяется метод вариации произвольных постоянных подобно ЛНДУ 1П (см. Л.52).
, то для его решения применяется метод вариации произвольных постоянных подобно ЛНДУ 1П (см. Л.52). , где
, где  – линейно независимые решения ДУ. В следующей лекции будут рассмотрены методы нахождения этих решений. Отметим наиболее важное:
– линейно независимые решения ДУ. В следующей лекции будут рассмотрены методы нахождения этих решений. Отметим наиболее важное: или
или  ;
;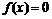 .
. .
. 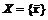 и
и  (см. лекцию № 5).
(см. лекцию № 5). , действующим из пространства
, действующим из пространства  в
в  в вектор
в вектор  , такой, что
, такой, что  есть результат воздействия оператора
есть результат воздействия оператора  .
.
 является оператором, действующим из одного множества в другое. Функционал так же является оператором или отображение любого линейного пространства в множество действительных чисел.
является оператором, действующим из одного множества в другое. Функционал так же является оператором или отображение любого линейного пространства в множество действительных чисел. и
и  и любых
и любых  верны условия:
верны условия:

 и
и 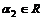



 .
. ), то оператор
), то оператор  . Оператор тождественного преобразования пространства.
. Оператор тождественного преобразования пространства. ,
,  .
. ,
, 
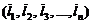 , (1)
, (1) справедливо разложение
справедливо разложение , (2)
, (2) – координата вектора
– координата вектора  (3)
(3)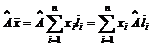 . (4)
. (4) подставим в (4) и получим
подставим в (4) и получим +
+ …
…


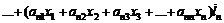 . (5)
. (5) .
. (6)
(6)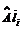 .
. – пространство непрерывных на отрезке
– пространство непрерывных на отрезке  функций
функций 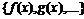 . Введем в этом пространстве оператор
. Введем в этом пространстве оператор 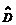 , такой что
, такой что  , т. е.
, т. е.  – дифференциальный оператор. Этот оператор является линейным. Известно, что
– дифференциальный оператор. Этот оператор является линейным. Известно, что  , а это соответствует определению.
, а это соответствует определению. – множестве функций, имеющих непрерывную производную до n-го порядка включительно, вводят оператор
– множестве функций, имеющих непрерывную производную до n-го порядка включительно, вводят оператор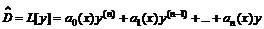 ,
,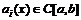 – множеству непрерывных функций.
– множеству непрерывных функций.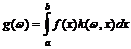 , (7)
, (7)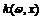 – фиксированная непрерывная функция, называемая ядром оператора. Такой оператор называется интегральным оператором. Если
– фиксированная непрерывная функция, называемая ядром оператора. Такой оператор называется интегральным оператором. Если  , то (7) называют косинус преобразованием,
, то (7) называют косинус преобразованием,  , то (7) называют синус преобразованием, если
, то (7) называют синус преобразованием, если  , то (7) называют Фурье преобразованием
, то (7) называют Фурье преобразованием . Пусть
. Пусть 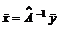 , где
, где  – оператор обратный
– оператор обратный  ,
, 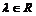 . (8)
. (8)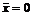 уравнения (8) называется тривиальным. Наличие ненулевых решений зависит от
уравнения (8) называется тривиальным. Наличие ненулевых решений зависит от  .
. , для которых существуют нетривиальные решения операторного уравнения (8), называются собственными числами или собственными значениями оператора
, для которых существуют нетривиальные решения операторного уравнения (8), называются собственными числами или собственными значениями оператора  , соответствующие собственным значениям, называются собственными векторами оператора
, соответствующие собственным значениям, называются собственными векторами оператора 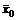 – собственный вектор оператора
– собственный вектор оператора 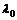 , то любой коллинеарный ему вектор, так же собственный, соответствующий тому же
, то любой коллинеарный ему вектор, так же собственный, соответствующий тому же  . Очевидно
. Очевидно  для любых
для любых  . Следовательно
. Следовательно  – собственный вектор оператора
– собственный вектор оператора  .
.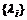 в
в 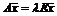 , где А – матрица линейного оператора (6), E – единичная матрица. Тогда
, где А – матрица линейного оператора (6), E – единичная матрица. Тогда  , откуда получим выражение
, откуда получим выражение , (9)
, (9) . (10)
. (10) , поэтому система может иметь единственное тривиальное решение если определитель матрицы коэффициентов
, поэтому система может иметь единственное тривиальное решение если определитель матрицы коэффициентов 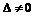 или иметь множество решений если
или иметь множество решений если  . Т. е.
. Т. е. (11)
(11) . (12)
. (12) . Найдем решение операторного уравнения (8). Согласно правилу
. Найдем решение операторного уравнения (8). Согласно правилу ,
, ,
, ,
,  ,
, – спектр оператора. Далее найдем собственные вектора
– спектр оператора. Далее найдем собственные вектора  . Для
. Для 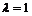 имеем
имеем 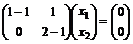 , откуда
, откуда  , следовательно
, следовательно  , а
, а 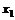 – любой. Пусть
– любой. Пусть  , тогда
, тогда 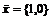 . Аналогично для
. Аналогично для  имеем
имеем  , откуда
, откуда  . Пусть
. Пусть 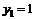 , тогда
, тогда  и
и  . Таким образом решением будет
. Таким образом решением будет  , т. е. n-мерное пространство в котором задано скалярное произведение (см. лекцию № 7).
, т. е. n-мерное пространство в котором задано скалярное произведение (см. лекцию № 7). и
и  выполняется равенство
выполняется равенство 
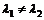 – собственные числа оператора
– собственные числа оператора 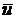 и
и 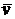 . Тогда
. Тогда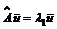 , (1)
, (1) . (2)
. (2) . Подставим (1, 2) и получим
. Подставим (1, 2) и получим  , откуда
, откуда  . Дале
. Дале  , т. е.
, т. е.  . Таким образом
. Таким образом  или
или  . Теорема доказана.
. Теорема доказана. .
.

 ,
, 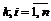 ,
,  .
. ,
,  .
. . Характеристическое уравнение
. Характеристическое уравнение  , тогда
, тогда ,
,  ,
, 
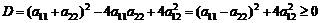
 ,
,  .
.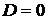 ,
,  . Но
. Но  ,
, 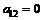 , тогда
, тогда  .
. . Решение операторного уравнения
. Решение операторного уравнения 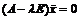
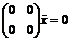
 любой. Теорема доказана.
любой. Теорема доказана.
 . В
. В  базисные вектора
базисные вектора  . Пусть
. Пусть  – базис по условию, в котором вектор
– базис по условию, в котором вектор (3)
(3)
 . (4)
. (4) (5)
(5)