
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дифференциальные уравнения первого порядка1. Задачи, приводящие к понятию дифференциального уравнения 2. Основные понятия дифференциального уравнения 3. Дифференциальные уравнения первого порядка, задача Коши 4. Дифференциальные уравнения первого порядка с разделенными и разделяющимися переменными 5. Однородные дифференциальные уравнения первого порядка Цель занятия: Изучить основные понятия дифференциальных уравнений, научиться классифицировать дифференциальные уравнения первого порядка и решать простейшие уравнения первого порядка. Роль и место лекции Этой лекцией начинается изучение нового раздела высшей математики «Дифференциальные уравнения». Из лекций, посвященных интегральному исчислению уже известно, что существуют задачи, при решении которых необходимо определять первообразные некоторых функций. При этом получают множество решений или множество первообразных. Другими словами получают общее решение. В некотором роде подобные задачи являются простейшим случаем решения дифференциальных уравнений. Если рассмотреть более сложные случаи, например, при наличии производных более высокого порядка, задание производной функции неявно, или сложное задание функции, а так же при необходимости отыскания частного или одного решения (первообразной) для определенных начальных условий, то мы определим задачи, которые решает раздел математики «Дифференциальные уравнения». Понимание данной лекции особенно важно, так как в ней рассмотрены основные понятия дифференциальных уравнений, которые будут необходимы на протяжении изучения всех лекций темы «Дифференциальные уравнения»  Вопрос № 1. Задачи, приводящие к понятию дифференциального уравнения 1.1. Прикладная задача Пусть некоторая популяция (сообщество особей одного вида) имеет в момент времени
1.2. Геометрическая задача Составить уравнение линии, проходящей, через точку Вопрос № 2. Основные понятия дифференциального уравнения Определение № 1. Дифференциальным уравнением называется уравнение, содержащее независимую переменную, функцию этой переменной ее производную или дифференциалы Определение № 2 . Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в это уравнение. В задаче № 1 приведено дифференциальное уравнение первого порядка, а выражение (1) дифференциальное уравнение n-го порядка. Определение № 3. Степенью дифференциального уравнения называется степень наивысшей производной, входящей в это уравнение. ПРИМЕР № 1.
Определение № 4. Решением дифференциального уравнения называется функция, которая вместе со своими производными обращает дифференциальное уравнение в тождественное равенство. Определение № 5.
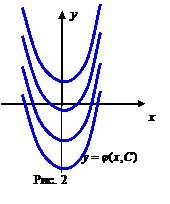
Определение № 6. Частным решением дифференциального уравнения, называется решение, полученное из общего при конкретных значениях произвольных постоянных. Они находятся из начальных условий при Некоторые дифференциальные уравнения имеют так же особое решение. Определение № 7. Особым решением называется такое, которое нельзя получить из общего ни при каких значениях произвольных постоянных. Геометрический смысл – огибающая семейства интегральных кривых (рис. 1). Замечание!!! Обыкновенные дифференциальные уравнения – есть уравнения относительно функции одной переменой. Дифференциальные уравнения многих переменных есть уравнение в частных производных.
Вопрос № 3. Дифференциальные уравнения первого порядка, задача Коши 3.1. Определение ДУ первого порядка Определение № 8.
Определение № 9. Общим решением дифференциального уравнения 1 – го порядка называется решение, содержащее одну произвольную постоянную Определение № 10. Частным решением дифференциального уравнения 1 – го порядка называется решение, полученное из общего при конкретном значении произвольной постоянной. Правило № 1. Частное решение находят из общего решения с помощью начальных условий при Замечание!!! Геометрически частное решение – одна из интегральных кривых, проходящая через заданную точку 3.2. Геометрический смысл ДУ первого порядка Запишем дифференциальное уравнение (ДУ) первого порядка в форме (3)
Множество точек с определенными направлениями, соответствующих (3), называется полем направлений дифференциального уравнения. Прямая, соединяющая все точки с одинаковым направлением называется изоклиной (рис. 4). ПРИМЕР № 2. Для уравнения 3.3. Задача Коши Определение № 12. Задача, состоящая в нахождении частных решений дифференциального уравнения первого порядка Теорема № 1 (существования и единственности решения задачи Коши). Если в уравнении
Вопрос № 4. Дифференциальные уравнения первого порядка с разделенными и разделяющимися переменными Если в выражении (4) функция P зависит только от x, а функция Q только от y, то дифференциальное уравнение будет уравнением с разделенными переменными Правило № 2. Чтобы найти общее решение ДУ с разделенными переменными надо его почленно проинтегрировать, а в правую часть поставить произвольную C. Если в уравнении (4) функции Пусть ПРИМЕР № 3. Решить дифференциальное уравнение Вопрос № 5. Однородные дифференциальные уравнения первого порядка Определение № 14. Функция ПРИМЕР № 4. Функция Определение № 15. ДУ 1-го порядка Преобразуем уравнение (4) к виду (3). Получим Определение № 16. ДУ 1-го порядка Для решения однородного дифференциального уравнения (ОДУ) преобразуем правую часть Вывод!!! В однородном уравнении
Это уравнение с помощью подстановки
Правило № 3. Чтобы найти общее решение однородного дифференциального уравнения первого порядка надо 1. С помощью подстановки 2. Разделить переменные и проинтегрировать уравнение. В полученных интеграл вместо ПРИМЕР № 5. Дано Заключение Поскольку в данной лекции были даны основные определения, то данный материал будет необходим практически при изучении всех последующих лекций, посвященных данной теме. При изучении данной лекции необходимо было обратить особое внимание на определения № 2, 3. 15, позволяющие классифицировать дифференциальные уравнения. Наиболее трудным для понимания вопросом является определения однородности уравнения. Поэтому рекомендуется еще раз разобрать приведенный пример № 4. Как было показано в первом вопросе, задачи, приводящие к необходимости решения дифференциальных уравнений, встречаются практически в любой прикладной области. В биологии, физики, социологии, экономики и др. областях, где возникает необходимость решения уравнений, в которые ходят функции некоторых процессов, скорости их роста, ускорения и так далее. Так же отметим: - в обыкновенные ДУ входят переменная, функция и производные; - в ДУ в частных производных входят частные производные; - порядок ДУ соответствует порядку наивысшей производной уравнения; - степень ДУ соответствует степени наивысшей производной уравнения; - в общем решении ДУ содержатся произвольные постоянные, число которых соответствует порядку ДУ; - частное решение находится из общего при конкретном значении постоянных; - задача Коши – нахождение частного решения ДУ 1-го порядка при начальных условиях; - ДУ с разделяющимися переменными решаются методом почленного интегрирования; - в однородном ДУ для правой части справедливо Литература 15. Баврин И.И. Высшая математика. – М.: Просвещение, 2003. – 384 с. 16. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. – Ростов-на-Дону: Феникс, 1997. – 512 с. 17. Демидович Б.П., Кудрявцев В.А.Краткий курс высшей математики. – М.: Астрель, 2001. - 656 с. Лекция № 52 |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 175. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 биомассу
биомассу  . Предположим, что в каждый момент времени скорость увеличения биомассы пропорциональна уже имеющейся биомассе, т. е.
. Предположим, что в каждый момент времени скорость увеличения биомассы пропорциональна уже имеющейся биомассе, т. е.  , а возникающие явления самоотравления снижают биомассу пропорционально квадрату наличной биомассы, т. е.
, а возникающие явления самоотравления снижают биомассу пропорционально квадрату наличной биомассы, т. е.  . Требуется определить количество биомассы в момент времени
. Требуется определить количество биомассы в момент времени  .
. Если обозначить биомассу в момент времени t через
Если обозначить биомассу в момент времени t через  , то можно записать дифференциальное уравнение
, то можно записать дифференциальное уравнение  или
или  . Проинтегрируем обе части
. Проинтегрируем обе части  , где С – произвольная постоянная, тогда
, где С – произвольная постоянная, тогда  ,
,  ,
,  . Поскольку
. Поскольку  , то
, то  , откуда
, откуда  . Подстановка в полученное выражение даст
. Подстановка в полученное выражение даст  . График этой функции представлен на рисунке. Его анализ показывает, что популяция стабилизируется, причем при
. График этой функции представлен на рисунке. Его анализ показывает, что популяция стабилизируется, причем при  популяция до стабилизации растет, а при
популяция до стабилизации растет, а при  вымирает.
вымирает. , у которой тангенс касательной для любого
, у которой тангенс касательной для любого  определяется согласно выражению
определяется согласно выражению  . По условию
. По условию  – дифференциальное уравнение. Последнее запишем как
– дифференциальное уравнение. Последнее запишем как  или
или  . Тогда
. Тогда  откуда уравнение кривой
откуда уравнение кривой 
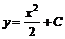 . По условию точка
. По условию точка  , поэтому
, поэтому 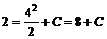 , откуда
, откуда  . Тогда искомое уравнение
. Тогда искомое уравнение  .
. или
или  . (1)
. (1) – уравнение третьего порядка и третьей степени.
– уравнение третьего порядка и третьей степени. Общим решением дифференциального уравнения называется решение, содержащее произвольные постоянные. Обозначается
Общим решением дифференциального уравнения называется решение, содержащее произвольные постоянные. Обозначается  или в явном виде
или в явном виде 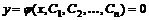 , где
, где 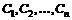 – произвольные постоянные, число которых соответствует порядку уравнения.
– произвольные постоянные, число которых соответствует порядку уравнения. ,
,  ,
,  ,…,
,…,  .
.  Дифференциальным уравнением 1 – го порядка называется уравнение, содержащее независимую переменную, функцию этой переменной и ее производную или дифференциал первого порядка.
Дифференциальным уравнением 1 – го порядка называется уравнение, содержащее независимую переменную, функцию этой переменной и ее производную или дифференциал первого порядка. Обозначается как
Обозначается как  (2) или в явном виде
(2) или в явном виде  (3). Если правую часть выражение (3) можно представить в виде отношения многочленов
(3). Если правую часть выражение (3) можно представить в виде отношения многочленов  , то выражение (3) можно представить в виде
, то выражение (3) можно представить в виде  . (4)
. (4) или
или  . Геометрический смысл – семейство интегральных кривых на плоскости (рис. 2).
. Геометрический смысл – семейство интегральных кривых на плоскости (рис. 2). ,
,  .
.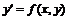 . Пусть функция
. Пусть функция  определена в области
определена в области  . Возьмем некоторую точку
. Возьмем некоторую точку  . Подставим в (3) и получим
. Подставим в (3) и получим  угла наклона касательной к интегральной кривой в этой точке. Аналогично для всех точек
угла наклона касательной к интегральной кривой в этой точке. Аналогично для всех точек  . Следовательно, уравнение (3) задает направление в каждой точке области D (рис. 3).
. Следовательно, уравнение (3) задает направление в каждой точке области D (рис. 3). Определение № 11.
Определение № 11. изоклиной будут окружности.
изоклиной будут окружности. , и его частная производная
, и его частная производная  ограничена в этой области, то существует единственная функция
ограничена в этой области, то существует единственная функция  – решение ДУ, удовлетворяющая начальным условиям
– решение ДУ, удовлетворяющая начальным условиям  .
. или
или  . Следовательно, функции отличаются только на произвольную постоянную. Проинтегрируем обе части равенства
. Следовательно, функции отличаются только на произвольную постоянную. Проинтегрируем обе части равенства  , тогда общим решением дифференциального уравнения с разделенными переменными будет
, тогда общим решением дифференциального уравнения с разделенными переменными будет . (5)
. (5) и
и  можно разложить на множители, каждый из которых зависит только от одной переменной, то это уравнение называется ДУ с разделяющимися переменными.
можно разложить на множители, каждый из которых зависит только от одной переменной, то это уравнение называется ДУ с разделяющимися переменными. , а
, а  . Тогда выражение (4) примет вид
. Тогда выражение (4) примет вид  . Разделим обе части на
. Разделим обе части на  и
и  и получим
и получим  уравнение с разделенными переменными. Решением такого уравнения будет согласно (5)
уравнение с разделенными переменными. Решением такого уравнения будет согласно (5)  .
. .
.



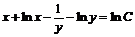 . Ответ
. Ответ  .
. .
. однородная, так как выполняется условие
однородная, так как выполняется условие  – однородное уравнение второго измерения. В свою очередь функция
– однородное уравнение второго измерения. В свою очередь функция  неоднородная.
неоднородная.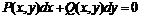 называется однородным, если функции P и Q однородны одного и того же измерения.
называется однородным, если функции P и Q однородны одного и того же измерения. 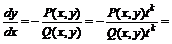
 . Таким образом, функция
. Таким образом, функция 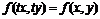 .
. и подставим
и подставим  . Тогда
. Тогда 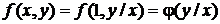 .
. . Следовательно, получим уравнение вида
. Следовательно, получим уравнение вида . (6)
. (6) приводится к уравнению с разделяющимися переменными. Покажем это. Найдем
приводится к уравнению с разделяющимися переменными. Покажем это. Найдем  . Подставим в (6)
. Подставим в (6)  . Разделим переменные U и x, т. е. уравнение
. Разделим переменные U и x, т. е. уравнение 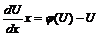 приведем к виду
приведем к виду  . Откуда получим общее решение
. Откуда получим общее решение 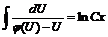 или
или  . С учетом
. С учетом  получим окончательное решение ОДУ
получим окончательное решение ОДУ  .
. привести это уравнение к уравнению с разделяющимися переменными.
привести это уравнение к уравнению с разделяющимися переменными. подставить
подставить  .
. – однородное ДУ 1-го порядка. Применим подстановку
– однородное ДУ 1-го порядка. Применим подстановку  . Откуда
. Откуда  или
или  . Проинтегрируем
. Проинтегрируем 

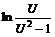 . Тогда
. Тогда  , откуда
, откуда  . Тогда решение
. Тогда решение  .
. .
.