
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Линейные дифференциальные уравнения первого порядка1. Линейные дифференциальные уравнения первого порядка. 2. Уравнение Бернулли 3. Уравнение в полных дифференциалах 4. Уравнения Лагранжа и Клеро, не разрешенные относительно производных Цель занятия: Изучить понятие линейного дифференциального уравнения и рассмотреть возможные их типы. Научиться классифицировать и решать дифференциальные уравнения первого порядка. Роль и место лекции Предыдущая лекция была посвящена основным терминам и понятиям дифференциальных уравнений. Для успешного решения дифференциальных уравнений особенно важно точно классифицировать его тип, поскольку это обуславливает выбираемый в этом случае метод решения. Ранее были рассмотрены достаточно простые однородные дифференциальные уравнения первого порядка с разделяющимися и разделенными переменными. Однако, как будет показано в этой лекции, дифференциальные уравнения могут быть и более сложного вида. Обращаем внимание на то, что не существует общего метода или способа решения дифференциальных уравнений, как их нет и при вычислении интегралов. То есть особую значимость играет правильность применения одного из методов, применимого для данного вида дифференциального уравнения. Материал данной лекции необходим при изучении линейных дифференциальных уравнений высших порядков. Вопрос № 1. Линейные дифференциальные уравнения первого порядка 1.1. Формы линейного ДУ 1-го порядка Определение № 1. Дифференциальное уравнение первого порядка, линейное относительно искомой функции и ее производной, называется линейным. Т. е. ДУ вида
где  1. Если 2. Если
3. Общий случай если 1.2. Метод подстановки Бернули В данном методе используется подстановка вида
где
В равенстве (3) одну из функций выбирают произвольно, так чтобы
1.3. Метод вариации произвольно постоянной Уже отмечалось, что линейно однородное уравнение (без правой части) или ЛОДУ
ПРИМЕР № 1. Найти общее решение линейного ДУ Вопрос № 2. Уравнение Бернулли Определение № 2. Уравнением Бернулли называется дифференциальное уравнение первого порядка вида где Данные уравнения можно привести к линейному виду, используя подстановку ПРИМЕР № 2. Найти частное решение ДУ Вопрос № 3. Уравнение в полных дифференциалах 3.1. Условие уравнения в полных дифференциалах и его общее решение Определение № 3. Дифференциальное уравнение 1-го порядка вида Обратите внимание, что левая часть имеет вид полного дифференциала. Поэтому если левая часть есть полный дифференциал некоторой функции, т. е. Вывод!!! ДУ 1-го порядка называется дифференциальным уравнение в полных дифференциалах, если выполняется (13).
ПРИМЕР № 3. Найти общее решение ДУ 3.2. Интегрирующий множитель Если условие (13) не выполняется, то это не уравнение в полных дифференциалах. Однако это уравнение иногда можно привести к уравнению в полных дифференциалах умножением его на некоторую функцию ПРИМЕР № 4. Решить уравнение Вопрос № 4. Уравнения Лагранжа и Клеро, не разрешенные относительно производных 4.1. Уравнение Лагранжа Определение № 4. Уравнением Лагранжа называется уравнение, не разрешенное относительно производной, вида где Для его решения используют вспомогательный параметр Замечание!!! При преобразованиях производилось деление на 4.2. Уравнение Клеро Определение № 5. Уравнение Клеро как частный случай уравнения Лагранжа называется уравнение, не разрешенное относительно производной, вида Для его решения используют так же вспомогательный параметр ПРИМЕР № 5. Решить уравнение Клеро Заключение В заключении отметим, что важно различать линейные уравнения. Так например уравнения Лагранжа и Клеро не линейные. Однако в основе их решений лежит решение линейных дифференциальных уравнений. Отметим так же появление особых решений в нелинейных дифференциальных уравнениях, которые не могут быть получены из общего решения. Очевидно, что в особых решениях отсутствует произвольная постоянная. Данная лекция была посвящена вопросам непосредственного решения конкретных типов ДУ, которые могут возникать при решении прикладных задач. Приведенные методы необходимо знать, так как они будут использованы при изучении следующих лекций. Отметим наиболее важное: - в ЛДУ 1-го порядка линейная зависимость относительно искомой функции и ее производной; - линейно однородное ДУ не содержит правой части; - ЛДУ решаются с помощью подстановки Бернулли - в уравнении Бернулли присутствует искомая функция в степени m, решается это уравнение либо приведением его к линейному виду подстановкой - в уравнении в полных дифференциалах разделены - уравнения Лагранжа и Клеро решаются с помощью подстановки Литература 18. Баврин И.И. Высшая математика. – М.: Просвещение, 2003. – 384 с. 19. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. – Ростов-на-Дону: Феникс, 1997. – 512 с. 20. Демидович Б.П., Кудрявцев В.А.Краткий курс высшей математики. – М.: Астрель, 2001. - 656 с. Лекция № 53 |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 228. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , (1)
, (1) и
и  – непрерывные функции. Возможны частные случаи.
– непрерывные функции. Возможны частные случаи. , то выражение (1) сводится к дифференциальному уравнению с разделяющимися переменными
, то выражение (1) сводится к дифференциальному уравнению с разделяющимися переменными  .
. , то выражение (1) сводится линейному дифференциальному уравнению без правой части
, то выражение (1) сводится линейному дифференциальному уравнению без правой части  или линейно однородному дифференциальному уравнению (ЛОДУ). В этом случае можно разделить переменные
или линейно однородному дифференциальному уравнению (ЛОДУ). В этом случае можно разделить переменные 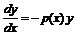 , откуда
, откуда  . Проинтегрируем обе части
. Проинтегрируем обе части 
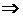

 решение
решение . (2)
. (2) и
и  используют один из двух методов.
используют один из двух методов. , (3)
, (3) и
и  – функции дифференцируемые по переменной x. Из выражения (3) следует
– функции дифференцируемые по переменной x. Из выражения (3) следует  . Последнее подставим в (1) и получим
. Последнее подставим в (1) и получим  , откуда
, откуда . (4).
. (4).  . Найти такую функцию просто, поскольку последнее является линейным ДУ без правой части (см п. 2.). Поэтому решение для
. Найти такую функцию просто, поскольку последнее является линейным ДУ без правой части (см п. 2.). Поэтому решение для  будет иметь вид (2), а именно
будет иметь вид (2), а именно 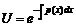 (5). Подставим (5) в (4) и получим уравнение
(5). Подставим (5) в (4) и получим уравнение  или
или  , которое является ДУ 1-го порядка с разделяющимися переменными. Его решение следующее
, которое является ДУ 1-го порядка с разделяющимися переменными. Его решение следующее

 (7). Тогда подстановка (7) и (5) в (3) даст общее решение ДУ (1)
(7). Тогда подстановка (7) и (5) в (3) даст общее решение ДУ (1)  . (8)
. (8) имеет общее решение вида (2)
имеет общее решение вида (2) 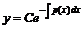 . Заменим произвольную постоянную C некоторой функцией
. Заменим произвольную постоянную C некоторой функцией  , т. е. предположим, что значение константы стало зависеть от текущей переменной. Тогда запишем
, т. е. предположим, что значение константы стало зависеть от текущей переменной. Тогда запишем  (9). Чтобы (9) было решением ЛНДУ (1) необходимо, чтобы она удовлетворяла ему. Найдем
(9). Чтобы (9) было решением ЛНДУ (1) необходимо, чтобы она удовлетворяла ему. Найдем  , подставим последнее в (1) и получим
, подставим последнее в (1) и получим  или
или  – это уравнение с разделяющимися переменными. Решая его, получим
– это уравнение с разделяющимися переменными. Решая его, получим 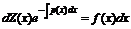 или
или  , откуда найдем
, откуда найдем  . Последнее подставим в выражение (9) и получим общее решение линейного ДУ 1-го порядка в виде
. Последнее подставим в выражение (9) и получим общее решение линейного ДУ 1-го порядка в виде . (10)
. (10) . Запишем его в форме (1)
. Запишем его в форме (1)  , откуда
, откуда  , а
, а  . Воспользуемся выражением (8) и запишем общее решение
. Воспользуемся выражением (8) и запишем общее решение  или
или  , тогда
, тогда  , откуда
, откуда 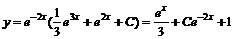 .
. , (11)
, (11) .
. . Однако на практике зачастую уравнения Бернулли не приводят к линейному виду а используют подстановку Бернулли.
. Однако на практике зачастую уравнения Бернулли не приводят к линейному виду а используют подстановку Бернулли. для
для  . Применим подстановку
. Применим подстановку  , тогда
, тогда  или
или  . Определим функцию V, такую что
. Определим функцию V, такую что 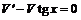 . Данное уравнение с разделяющимися переменными. Разделим переменные
. Данное уравнение с разделяющимися переменными. Разделим переменные  . Интегрируя обе части равенства получим
. Интегрируя обе части равенства получим  , откуда
, откуда  . Подставим последнее в исходное уравнение
. Подставим последнее в исходное уравнение  , откуда
, откуда 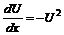 . Разделим переменные
. Разделим переменные  и проинтегрируем
и проинтегрируем  или
или 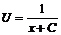 . С учетом подстановки получим
. С учетом подстановки получим  . Подставим начальные условия и определим свободную переменную
. Подставим начальные условия и определим свободную переменную 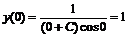 , откуда
, откуда  . Тогда частное решение
. Тогда частное решение 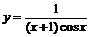 .
. 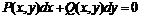 называется уравнением в полных дифференциалах (УПД).
называется уравнением в полных дифференциалах (УПД).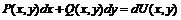 , то
, то  , что соответствует
, что соответствует  (12). Тогда по определению полного дифференциала
(12). Тогда по определению полного дифференциала  или
или  ,
,  . Определим вторые смешанные частные производные
. Определим вторые смешанные частные производные  ,
,  . По определению смешанные производные равны, следовательно левые части этих равенств равны, поэтому
. По определению смешанные производные равны, следовательно левые части этих равенств равны, поэтому  (13).
(13). Вместо одной произвольной постоянной используем начальную точку интегрирования, т. е. выберем пределы интегрирования, текущие
Вместо одной произвольной постоянной используем начальную точку интегрирования, т. е. выберем пределы интегрирования, текущие  ,
,  и начальные
и начальные  . Представим эти точки графически (рис. 1). Интегрирование полного дифференциала
. Представим эти точки графически (рис. 1). Интегрирование полного дифференциала 
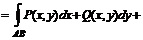
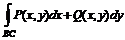 . Очевидно
. Очевидно 
 , а
, а 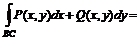
 . Тогда
. Тогда 
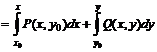 откуда согласно (12) получим общее решение ДУ в ПД
откуда согласно (12) получим общее решение ДУ в ПД . (14)
. (14) . Пусть
. Пусть 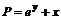 , а
, а  . Видно, что
. Видно, что  и
и  , следовательно, это уравнение в полных дифференциалах. Возьмем начальную точку
, следовательно, это уравнение в полных дифференциалах. Возьмем начальную точку  , тогда согласно (14) общее решение будет иметь вид
, тогда согласно (14) общее решение будет иметь вид  , или
, или  .
. , называемую интегрирующим множителем. Чтобы ее найти необходимо, чтобы уравнение
, называемую интегрирующим множителем. Чтобы ее найти необходимо, чтобы уравнение  было уравнением в полных дифференциалах, то есть для него выполнялось условие (13)
было уравнением в полных дифференциалах, то есть для него выполнялось условие (13)  . Выполнив дифференцирование
. Выполнив дифференцирование 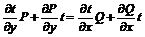 и приведя подобные слагаемые, получим
и приведя подобные слагаемые, получим  . Для нахождения
. Для нахождения  . Тогда последнее уравнение примет вид
. Тогда последнее уравнение примет вид  или
или  , откуда
, откуда  . Аналогично получим для
. Аналогично получим для  . При этом подынтегральные выражения должны зависеть только от x или y соответственно.
. При этом подынтегральные выражения должны зависеть только от x или y соответственно. . Здесь
. Здесь 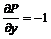 и
и  . Т. е. (13) не выполняется. Однако
. Т. е. (13) не выполняется. Однако  зависит только от x. Следовательно, интегрирующий множитель
зависит только от x. Следовательно, интегрирующий множитель 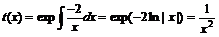 . Умножая исходное уравнение на этот множитель, получим
. Умножая исходное уравнение на этот множитель, получим 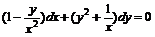 уравнение в полных дифференциалах. Решая его согласно (14) получим
уравнение в полных дифференциалах. Решая его согласно (14) получим  .
. , (15)
, (15) и
и  известные функции от
известные функции от 
 . Тогда уравнение (15) примет вид
. Тогда уравнение (15) примет вид  . Дифференцируя его по x, получим
. Дифференцируя его по x, получим  , то есть
, то есть  (16) или
(16) или  или
или  (см. (1)). Данное уравнение есть линейное ДУ относительно неизвестной функции
(см. (1)). Данное уравнение есть линейное ДУ относительно неизвестной функции 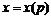 . Решая это уравнение согласно (8) или (10) получим некоторое решение в виде
. Решая это уравнение согласно (8) или (10) получим некоторое решение в виде  . Исключая параметр p, получим общий интеграл уравнения (15) в виде некоторой функции
. Исключая параметр p, получим общий интеграл уравнения (15) в виде некоторой функции 
 , поэтому было потеряно решение, для которого
, поэтому было потеряно решение, для которого 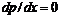 , то есть для некоторого значения
, то есть для некоторого значения 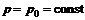 . Очевидно из (16) это значение есть корень уравнения
. Очевидно из (16) это значение есть корень уравнения  , поэтому решение
, поэтому решение  есть особое решение.
есть особое решение. , (17)
, (17) . Дифференцируя его по x, получим
. Дифференцируя его по x, получим  , то есть
, то есть  . Если
. Если  , то
, то 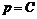 . Поэтому общее решение уравнения (17) имеет вид
. Поэтому общее решение уравнения (17) имеет вид  (18). Однако так же может выполняться и
(18). Однако так же может выполняться и 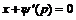 . Получаем частное решение в параметрической форме
. Получаем частное решение в параметрической форме  (19) – это особое решение уравнения Клеро.
(19) – это особое решение уравнения Клеро. . Общее решение будет иметь вид (18)
. Общее решение будет иметь вид (18)  . Особое решение получаем согласно (19)
. Особое решение получаем согласно (19)  , откуда следует
, откуда следует  .
. ;
;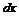 и
и  и нет правой части, так же должно выполнятся условие (13);
и нет правой части, так же должно выполнятся условие (13);  .
.