
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Разложение функции в степенные рядыСтр 1 из 5Следующая ⇒ Лекция № 44 Числовые ряды 1. Понятия числового ряда 2. Ряд геометрической прогрессии 3. Необходимый признак сходимости числового ряда 4. Остаток ряда и его свойства 5. Свойства сходящихся рядов Цель занятия: Изучить понятие числового ряда. Научиться классифицировать числовой ряд по необходимому признаку. Роль и место лекции В повседневной жизни нам практически постоянно приходится сталкиваться с понятием «ряд», начиная от абстрактных понятий как «ряд неудач» и кончая бытовыми примерами, например эквалайзер вашего магнитофона. Даже привычные вещи непосредственно связаны с понятием рядов. Например, прирост населения страны, рост популяции животных, индекс деловой активности и др. есть числовые или функциональные последовательности, т. е. ряды. Одни ряды конечные, другие бесконечные. Простой белый свет есть бесконечная сумма квантов с различной длиной волны, т. е. сумма цветов радуги дает белый свет, и т.д. Вам уже знакомо понятие числовой последовательности как функции натурального аргумента из теории пределов по второму замечательному пределу. Это пример как бесконечная сумма чисел имеет предел равный экспоненте. Для лучшего изучения данной темы необходимо повторить раздел «Теория пределов». Данной лекцией начинается тема «Ряды». Ее задача дать основные понятия, необходимые для дальнейшего изучения данной темы, а так же обобщить известные ранее, но разрозненные понятия. Вопрос № 1. Понятия числового ряда Напомним, что числовая последовательность – это функция натурального аргумента. Отображение Определение № 1.  Аналитическое выражение вида называется числовым рядом, где ПРИМЕР № 1. 1. 2. 3.
Определение № 2. Сумма “n” первых членов числового ряда называется n-ой частной (частичной) суммой ряда Вывод!!! Запишем частные суммы Определение № 3. Конечный предел последовательности частных сумм числового ряда называется суммой этого ряда. Если этот конечный предел существует, то ряд называется сходящимся, а если не существует или равен бесконечности, то ряд называется расходящимся
ПРИМЕР № 2. Сходится ли ряд Вопрос № 2. Ряд геометрической прогрессии Рассмотрим наиболее часто встречающийся ряд вида ряд геометрической прогрессии. Для 1. 2. 3. 4. Вопрос № 3. Необходимый признак сходимости числового ряда Теорема № 1 (необходимый признак сходимости). Если ряд сходится, то общий член ряда стремиться к нулю при Доказательство. Составим частные суммы ряда Замечание!!! Обратное утверждение не верно. Т. е. если Следствие!!! Если ПРИМЕ № 3. Для Вопрос № 4. Остаток ряда и его свойства Запишем числовой ряд в виде Определение № 4. Бесконечный ряд, полученный отбрасыванием Теорема № 2. Если данный ряд сходится, то и его остаток также сходится. Составим суммы Теорема № 3. Если остаток числового ряда сходится, то и его числовой ряд также сходится. Доказательство. Составим суммы Следствие!!! Если ряд сходится, то Важно!!! Смысл теорем 2 и 3 состоит в том, что отбрасывание или приписывание конечного числа членов ряда не влияет на его сходимость. Вопрос № 5. Свойства сходящихся рядов Свойство № 1. Если все члены числового ряда Доказательство. Обозначим частную сумму исходного ряда Свойство № 2. Сходящиеся ряды можно почленно складывать, при этом сумма нового ряда равна сумме сумм первых рядов Важно!!! На все сходящиеся ряды можно перенести свойства конечных сумм. Заключение В заключении отметим, что понимание теории рядов особенно необходимо при решении многих прикладных задач, отмеченных вначале. Знание данного материала крайне необходимо для дальнейшего изучения темы «Ряды». Отметим наиболее важное: - ряды бывают конечные и бесконечные; - если сумма ряда бесконечна, то он расходится; - сумма ряда определяется пределом частной суммы; - если ряд сходится, то общий член ряда стремится к нулю при - даже если общий член ряда стремится к нулю, сам ряд может расходиться; - остаток ряда получается отбрасыванием первых членов ряда; - ряд сходится или расходится вместе со своим остатком; - на расходящиеся ряды нельзя перенести свойства конечных сумм. Литература 1. Баврин И.И. Высшая математика. – М.: Просвещение, 2003. – 384 с. 2. Воробьев Н.Н. Теория рядов. – М: Наука, 1996.– 408 с. - Лекция № 45 Знакоположительные ряды 1. Ряды с положительными членами 2. Признак сравнения как признак сходимости ряда 3. Признаки Даламбера и Коши 4. Интегральный признак сходимости Цель занятия: Научиться применять признаки сравнения, Даламбера, Коши и интегральный для определения сходимости знакоположительного ряда. Роль и место лекции На предыдущей лекции было изучено понятие ряда, рассмотрены числовые ряды общего вида. Как было показано определение их сходимости достаточно трудоемкая задача. Однако если ограничиться случаем знакоположительного ряда, то можно получить дополнительные, более простые аналитические выражения, позволяющие определить сходимость числового ряда. Для лучшего понимания данной лекции, рекомендуется повторить материал по теме «Пределы» и «Определенные интегралы». Данная лекция будет необходима при изучении лекции «Функциональные ряды» и «Ряды Фурье». Вопрос № 1. Ряды с положительными членами Определение № 1. Числовой ряд, все члены которого неотрицательны, называется рядом с положительными знаками или знакоположительным рядом. знакополижительный ряд если для любых Следствие!!! Ряд Теорема № 1. Для того чтобы знакоположительный ряд сходился необходимо и достаточно чтобы ряд частных сумм Доказательство (необходимость). Дан сходящийся ряд (1). Требуется доказать, что Доказательство (достаточность). Дано Замечание!!! Если ряд расходится, то Вопрос № 2. Признак сравнения как признак сходимости ряда Теорема № 2. Если для знакоположительных рядов Доказательство. Так как отбрасывание конечного числа членов ряда не влияет на его сходимость, то предположим, что, начиная с Пусть ряд ПРИМЕР № 1. Исследовать сходимость ряда Теорема № 3. Если для знакоположительных рядов Т. е. если ПРИМЕР № 2. Исследовать сходимость ряда Замечание!!! Обратите внимание на схожесть с методом сравнения бесконечно малых величин. Вопрос № 3. Признаки Даламбера и Коши Теорема № 4 (признак Даламбера). Если для знакоположительного ряда (1) существует предел 1. 2. 3. Доказательство. По определению предела последовательности следует, что
Пусть
Правая часть выражения (3) есть члены сходящегося ряда геометрической прогрессии Пусть ПРИМЕР № 3. Исследовать сходимость ряда Теорема № 5 (признак Коши). Если для знакоположительного ряда (1) существует предел 1. 2. 3. Вопрос № 4. Интегральный признак сходимости Дан ряд (1). Пусть функция Теорема № 6. Если функция ПРИМЕР № 4.
Определение № 2. Обобщенным гармоническим рядом называется ряд вида Исследуем сходимость обобщенного гармонического ряда. 1. 2. 3. 4.1. Правило исследования числового ряда 1. Выяснить знаком ли ряд. 2. Проверить необходимый признак сходимости 3. Проверить признаки сравнения, Даламбера, Коши или интегральный признак.
Заключение Отметим наиболее важное: - - если ряд расходится, то - признак Даламбера сравнивает последующие члены ряда; - признак Коши исследует корень n-й степени общего члена ряда; - интегральный признак применим, если общий член ряда задан функционально; - признак сравнения основан на сравнении рядов с известными свойствами; - гармонический ряд есть частный случай обобщенного гармонического ряда. Литература 3. Баврин И.И. Высшая математика. – М.: Просвещение, 2003. – 384 с. 4. Воробьев Н.Н. Теория рядов. – М: Наука, 1996.– 408 с. - Лекция № 46 Знакопеременные ряды 1. Абсолютно сходящиеся ряды 2. Признаки Даламбера, Коши и сравнения 3. Знакочередующиеся ряды 4. Свойства абсолютно сходящихся рядов Цель занятия: Научиться определять сходимости знакопеременного ряда. Роль и место лекции Данная лекция является продолжением предыдущей. Очевидно, что ряд может состоять из членов, меняющих свой знак. В этом случае рад может сходится несмотря на то, что тот же ряд, составленный из абсолютных величин, может расходится. Данным вопросам и посвящена эта лекция. Если в предыдущей лекции были рассмотрены только знакоположительные ряды, были получены признаки их сходимости, то на данной лекции будет рассмотрен общий случай знакопеременных рядов, а так же признаки их сходимости. Вопрос № 1. Абсолютно сходящиеся ряды Определение № 1. Числовой ряд, среди членов которого бесконечное множество положительных и бесконечное число отрицательных членов, называется знакопеременным рядом или рядом с произвольным членом. ПРИМЕР № 1. Теорема № 1 (достаточный признак сходимости знакопеременного ряда). Если ряд, составленный из абсолютных величин членов знакопеременного ряда, сходится, то данный ряд так же сходится. Если
Доказательство. Обозначим n-ю частную сумму ряда Обозначим сумму всех положительных членов правой части равенства (3) как
Поскольку Замечание!!! Теорема выражает достаточное, но не необходимое условие сходимости, то есть существуют сходящиеся знакопеременные ряды, для которых абсолютный ряд из Определение № 2. Знакопеременный ряд называется абсолютно или безусловно сходящимся если сходится ряд, составленный из абсолютных величин его членов. ПРИМЕР № 2. Ряд Определение № 3. Знакопеременный ряд называется относительно или условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится. Абсолютная сходимость обеспечивается быстрым стремлением к нулю, а условная сходимость обеспечивается интерференцией положительных и отрицательных членов. ПРИМЕР № 3. Ряд Вопрос № 2. Признаки Даламбера, Коши и сравнения Теорема № 2 (признак Даламбера). Если для знакопеременного ряда существует предел 1. 2. 3.
Теорема № 3 (признак Коши). Если для знакопеременного ряда существует предел 2. 3. Теорема № 4. Если для знакопеременного ряда Вопрос № 3. Знакочередующиеся ряды Определение № 4. Числовой ряд, в котором за положительным членом следует отрицательный и за отрицательным членом следует положительный член, называется знакочередующимся рядом. Теорема № 5 (Лейбница, признак сходимости знакочередующегося ряда). Если члены знакочередующегося ряда не возрастают по абсолютной величине и общий член ряда стремиться к нулю при Доказательство. Дан ряд ПРИМЕР № 4. Ряд Замечание!!! Теорема Лейбница используется для оценки погрешности. Известно, что ПРИМЕР № 5. Найти сумму
Вопрос № 4. Свойства абсолютно сходящихся рядов Замечание!!! Все абсолютно сходящиеся ряды обладают свойствами конечных сумм. Свойство № 1. Если все члены абсолютно сходящегося ряда Свойство № 2. Абсолютно сходящиеся ряды можно почленно складывать, при этом сумма нового ряда равна сумме сумм первых рядов Свойство № 3. В абсолютно сходящихся рядах можно переставлять члены Свойство № 4. В абсолютно сходящихся рядах можно группировать члены Теорема № 6 (Римана). В условно сходящемся ряде можно так переставить члены, что сумма ряда изменится или ряд станет расходящимся. ПРИМЕР № 6. Дан Заключение Отметим наиболее важное: - если ряд, составленный из абсолютных величин членов знакопеременного ряда, сходится, то данный ряд так же сходится; - если расходится ряд из абсолютных членов, то ряд условно сходящийся; - признак Даламбера и Коши отличается наличием знака модуля; - теорема Лейбница позволяет определить сходимость знакочередующегося ряда; - все абсолютно сходящиеся ряды обладают свойствами конечных сумм; - в условно сходящемся ряде переставлять члены нельзя. Литература 5. Баврин И.И. Высшая математика. – М.: Просвещение, 2003. – 384 с. 6. Воробьев Н.Н. Теория рядов. – М: Наука, 1996.– 408 с. -
Лекция № 47 Функциональные ряды 1. Понятие функционального ряда 2. Равномерная сходимость функционального ряда 3. Свойства равномерно сходящихся функциональных рядов 4. Степенные ряды, теорема Абеля Цель занятия: Изучить понятие функционального ряда. Научится классифицировать функциональные ряды. Исследовать степенной ряд. Роль и место лекции В предыдущих лекциях были рассмотрены числовые ряды как функция натурального аргумента. Вы знаете, что функция может быть сложной. То есть члены числового ряда в свою очередь могут быть функциями, причем общего вида. Тогда получим не числовой, а функциональный ряд, суммой которого будет не число, а некоторая другая функция. Подобные ряды наиболее часто встречаются в окружающем нас мире. Так музыка есть сумма отдельных звуков, описываемых некоторыми функциями. Очевидно, что функциональные ряды могут быть так же бесконечны. Есть даже отдельный раздел математики «Гармонический анализ», занимающийся исследованием разложений функций. Этим вопросам будут посвящены следующие несколько лекций. На данной лекции будут рассмотрены основные понятия и теоремы, необходимые для дальнейшего изучения теории рядов. Вопрос № 1. Понятие функционального ряда Определение № 1. Бесконечный ряд, членами которой являются функции вещественной или комплексной переменной, определенные в некоторой области D называется функциональным рядом.
ПРИМЕР № 1. Функциональный ряд Определение № 2. Точка, в которой функциональный ряд превращается в сходящийся числовой ряд, называется точкой сходимости функционального ряда. Определение № 3. Совокупность всех точек сходимости функционального ряда называется областью сходимости функционального ряда, и обозначается Рассмотрим ряд степенных функций или геометрической прогрессии с
Если
сходится на интервале Вывод!!! Сумма функционального ряда Вопрос № 2. Равномерная сходимость функционального ряда Область сходимости функционального ряда Определение № 4. Функциональный ряд называется равномерно сходящимся в области Теорема № 1 (Вейерштрасса, достаточный признак равномерной сходимости). Если для функционального ряда Доказательство. Абсолютная сходимость следует из условия (5) и признака сравнения. Ряд (5) сходится по условию, следовательно Важно!!! Существуют функциональные ряды, для которых не выполняется условие (5), однако они равномерно сходятся. Определение № 5. Функциональный ряд Вывод!!! Из признака Вейерштрасса следует, что любой мажорируемый ряд сходится равномерно, но не для всякого равномерно сходящегося ряда можно найти мажоранту. ПРИМЕР № 2. Дан ряд Вопрос № 3. Свойства равномерно сходящихся функциональных рядов Равномерно сходящиеся функциональные ряды обладают всеми свойствами конечных сумм функций. Напомним эти свойства. 1. Сумма конечного числа непрерывных функций есть функция непрерывная. 2. 4. Тогда свойства равномерно сходящихся рядов будут следующие. Свойство № 1. Если функциональный ряд Свойство № 2. Если функциональный ряд (1) равномерно сходится в области Свойство № 3. Если функциональный ряд (1) равномерно сходится в области Свойство № 4. Если функциональный ряд (1) равномерно сходится на Вопрос № 4. Степенные ряды, теорема Абеля Определение № 6. Функциональный ряд
называется степенным рядом или рядом по степеням двучлена Если параметр
по степеням переменной Теорема № 2 (Абеля). Для всякого степенного ряда Доказательство. Для любых Число называется радиусом сходимости степенного ряда (7). В точках
Если ПРИМЕР № 3.
Заключение Отметим наиболее важное: - числовой ряд – это частный случай функционального ряда; - в области сходимости функционального ряда значение его суммы - равномерно сходящийся ряд имеет остаток, уменьшающийся за счет уменьшения членов ряда, а не их интерференции; - признак Вейерштрасса - достаточный признак сходимости функционального ряда; - радиус сходимости степенного ряда определяется теоремой Абеля.
Литература 7. Баврин И.И. Высшая математика. – М.: Просвещение, 2003. – 384 с. 8. Воробьев Н.Н. Теория рядов. – М: Наука, 1996.– 408 с. - Лекция № 48 Разложение функции в степенные ряды 1. Свойства степенных рядов 2. Ряды Тейлора и Маклорена 3. Теоремы о разложимости функции в степенной ряд 4. Разложение элементарных функций в степенные ряды 5. Степенные ряды в комплексной области Цель занятия: Изучить ряды Тейлора и Маклорена. Научиться раскладывать в эти ряд |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 201. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 на
на  . Обозначается
. Обозначается  или
или  .
. (1)
(1) – члены числового ряда, если “n” не фиксирована, то
– члены числового ряда, если “n” не фиксирована, то  – общий член ряда.
– общий член ряда. – натуральный ряд.
– натуральный ряд. – ряд геометрической прогрессии
– ряд геометрической прогрессии  .
. – гармонический ряд.
– гармонический ряд. .
. ,
,  ,
,  и т. д. Тогда согласно определению № 1 следует, что любому числовому ряду соответствует еще одна последовательность числовых сумм
и т. д. Тогда согласно определению № 1 следует, что любому числовому ряду соответствует еще одна последовательность числовых сумм  .
.  .
. . Частная сумма
. Частная сумма  . Разложим на простейшие
. Разложим на простейшие 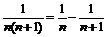 , тогда частная сумма
, тогда частная сумма  . Найдем предел
. Найдем предел 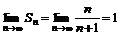 . Следовательно ряд сходящийся и сумма ряда
. Следовательно ряд сходящийся и сумма ряда  .
. , (2)
, (2) частная сумма
частная сумма  . Для различных значений параметра q возможны следующие варианты.
. Для различных значений параметра q возможны следующие варианты. , тогда
, тогда  и ряд сходится и
и ряд сходится и  .
. , тогда
, тогда  и ряд расходится.
и ряд расходится. , тогда
, тогда  и
и  – ряд расходится.
– ряд расходится. , тогда
, тогда 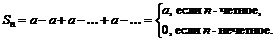 Следовательно предел
Следовательно предел  не существует (
не существует (  ) и ряд расходится. Таким образом
) и ряд расходится. Таким образом , (3)
, (3) .
. . Найдем
. Найдем  и предел
и предел 
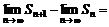 (по определению 2)=
(по определению 2)=  .
. не следует, что и весь ряд сходится. Например, гармонический ряд
не следует, что и весь ряд сходится. Например, гармонический ряд  расходится, а
расходится, а  .
. , то числовой ряд расходится.
, то числовой ряд расходится. запишем
запишем  . Следовательно, ряд расходится.
. Следовательно, ряд расходится. . (4)
. (4) первых членов, называется остатком числового ряда. Если этот ряд сходится, то его сумму обозначают, как
первых членов, называется остатком числового ряда. Если этот ряд сходится, то его сумму обозначают, как  , где
, где 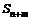 и
и  . Очевидно, что
. Очевидно, что  –
– 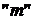 частная сумма ряда. По условию ряд сходится, поэтому
частная сумма ряда. По условию ряд сходится, поэтому  и
и  . Найдем
. Найдем  – остаток ряда так же сходится.
– остаток ряда так же сходится. . Найдем
. Найдем  . По условию остаток сходится
. По условию остаток сходится  . Из теоремы 2
. Из теоремы 2  . Тогда
. Тогда  – число, следовательно, ряд так же сходится.
– число, следовательно, ряд так же сходится. .
. умножить на одно и тоже число
умножить на одно и тоже число  , то вновь полученный ряд
, то вновь полученный ряд  будет сходиться или расходится вместе с исходным рядом, причем его сумма будет равны
будет сходиться или расходится вместе с исходным рядом, причем его сумма будет равны  .
. . Перейдем к пределу. Если
. Перейдем к пределу. Если  , то
, то  . Очевидно, что если
. Очевидно, что если  и
и  , то
, то  и новый ряд сходится или расходится вместе с исходным.
и новый ряд сходится или расходится вместе с исходным. ,
,  ,
,  .
. ;
; (1)
(1) справедливо
справедливо  .
. . Поскольку ряд знакоположителный, то
. Поскольку ряд знакоположителный, то  для любых
для любых  и
и  .
.  начиная с некоторого номера выполняется соотношение
начиная с некоторого номера выполняется соотношение  , то из сходимости второго ряда следует сходимости первого и из расходимости первого ряда следует расходимость второго ряда.
, то из сходимости второго ряда следует сходимости первого и из расходимости первого ряда следует расходимость второго ряда. , выполняется неравенство
, выполняется неравенство  следует неравенство
следует неравенство  . Пусть
. Пусть  – ограничена сверху. Но тогда в силу
– ограничена сверху. Но тогда в силу 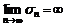 и ряд
и ряд  . Для этого сравним его с геометрическим рядом при
. Для этого сравним его с геометрическим рядом при  , т. е. с рядом
, т. е. с рядом  . Начиная с
. Начиная с 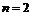 , выполняется неравенство
, выполняется неравенство  . Тогда в силу сходимости геометрического ряда и теоремы 2 следует, что заданный ряд сходится.
. Тогда в силу сходимости геометрического ряда и теоремы 2 следует, что заданный ряд сходится. , то оба ряда сходятся или расходятся одновременно.
, то оба ряда сходятся или расходятся одновременно. и второй ряд сходится, то и первый ряд сходится, а если
и второй ряд сходится, то и первый ряд сходится, а если  и второй ряд расходится, то и первый ряд расходится.
и второй ряд расходится, то и первый ряд расходится. . Сравним данный ряд с гармоническим рядом.
. Сравним данный ряд с гармоническим рядом.  . Тогда в силу того, что второй (гармонический) ряд расходится и теоремы 3 первый ряд так же расходится.
. Тогда в силу того, что второй (гармонический) ряд расходится и теоремы 3 первый ряд так же расходится. и
и , то ряд (1) сходится.
, то ряд (1) сходится. , то ряд (1) расходится.
, то ряд (1) расходится. , то сомнительный случай.
, то сомнительный случай. выполняется неравенство
выполняется неравенство  или
или . (2)
. (2) . Обозначим
. Обозначим  . Тогда, начиная с некоторого значения
. Тогда, начиная с некоторого значения  , из правой части (2) справедливо
, из правой части (2) справедливо  или
или 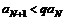 . Умножая обе части на
. Умножая обе части на  запишем
запишем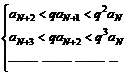 . (3)
. (3) при
при  . По правилу сравнения ряд (1) сходится.
. По правилу сравнения ряд (1) сходится. . Тогда из левой части (2) справедливо
. Тогда из левой части (2) справедливо  или
или  . Следовательно,
. Следовательно,  и ряд расходится.
и ряд расходится. . Запишем
. Запишем  ,
,  . Признак
. Признак  . Ряд сходится.
. Ряд сходится. и
и , то ряд (1) сходится.
, то ряд (1) сходится. , то ряд (1) расходится.
, то ряд (1) расходится. , то сомнительный случай.
, то сомнительный случай. определена на
определена на  , причем
, причем  ,
,  ,
,  … ,
… ,  .
. непрерывная, неотрицательная и убывающая, то ряд
непрерывная, неотрицательная и убывающая, то ряд  сходится или расходится вместе с несобственным интегралом
сходится или расходится вместе с несобственным интегралом 
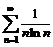 . Признак
. Признак  , ряд расходится
, ряд расходится , где
, где  .
. – гармонический ряд расходится
– гармонический ряд расходится  .
. – интегральный признак
– интегральный признак 
 и ряд расходится.
и ряд расходится. – интегральный признак
– интегральный признак 
 – конечное число и ряд сходится. Итак
– конечное число и ряд сходится. Итак . (4)
. (4) .
.
 сходится, то (1)
сходится, то (1) так же сходится. (2)
так же сходится. (2)  . Так как ряд (2) сходится, то существует предел
. Так как ряд (2) сходится, то существует предел  . Обозначим n-ю частную сумму ряда
. Обозначим n-ю частную сумму ряда  , а сумму абсолютных величин отрицательных членов через
, а сумму абсолютных величин отрицательных членов через  . Очевидно
. Очевидно . (4)
. (4) и
и  , то существует предел
, то существует предел  и предел
и предел 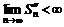 . Перейдем в (4) к пределу
. Перейдем в (4) к пределу 

 расходится.
расходится. из примера № 1 сходится. Составим ряд из его абсолютных членов
из примера № 1 сходится. Составим ряд из его абсолютных членов  . По признаку Даламбера
. По признаку Даламбера  этот ряд сходится, следовательно, исходный ряд сходится абсолютно.
этот ряд сходится, следовательно, исходный ряд сходится абсолютно. сходится, так как ряд
сходится, так как ряд  сходится (см. л. 45) и
сходится (см. л. 45) и  (признак сравнения). Однако ряд, составленный из абсолютных величин
(признак сравнения). Однако ряд, составленный из абсолютных величин  и
и и 1.
и 1.  , то ряд
, то ряд  сходится абсолютно
сходится абсолютно . (5)
. (5) , то ряд сходится, его сумма положительна и не превосходит первого члена.
, то ряд сходится, его сумма положительна и не превосходит первого члена. (6) ,
(6) ,  (7),
(7),  . Составим четную частную сумму
. Составим четную частную сумму  . По условию (7)
. По условию (7) 

 , следовательно,
, следовательно,  возрастает при
возрастает при 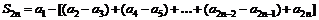 . Следовательно
. Следовательно  , возрастающая, положительная и ограниченная. Тогда существует предел
, возрастающая, положительная и ограниченная. Тогда существует предел  . Теперь возьмем нечетную частную сумму
. Теперь возьмем нечетную частную сумму  и перейдем к пределу
и перейдем к пределу  по условию (8).
по условию (8). сходится так как
сходится так как  и
и  , где
, где  знакопеременный, сходящийся ряд. Тогда по теореме Лейбница
знакопеременный, сходящийся ряд. Тогда по теореме Лейбница  (9). Следовательно за сумму ряда приближенно можно взять n первых членов и погрешность не будет превышать
(9). Следовательно за сумму ряда приближенно можно взять n первых членов и погрешность не будет превышать  .
. с точностью
с точностью  . Выполняются условия теоремы Лейбница
. Выполняются условия теоремы Лейбница 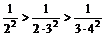 ,
,  и ряд сходится. Тогда
и ряд сходится. Тогда  . Поскольку
. Поскольку  , то
, то 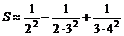 .
. .
.
 ,
,  .
. .
. условно сходящийся ряд. Сумма
условно сходящийся ряд. Сумма  ,
,  или
или 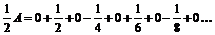 . Сложим с начальной суммой
. Сложим с начальной суммой  . При перестановке членов сумма изменилась.
. При перестановке членов сумма изменилась. . (1)
. (1) определен на
определен на  . Подставив любое значение
. Подставив любое значение  в ряд, получим числовой ряд , который может сходится или нет.
в ряд, получим числовой ряд , который может сходится или нет. если
если  ряд сходится,
ряд сходится, 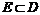 если не для всех
если не для всех  ряд сходится и
ряд сходится и 
 если
если 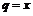
 . (2)
. (2) , ряд сходится (см. л. 44). Область сходимости
, ряд сходится (см. л. 44). Область сходимости 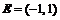 . В этом случае сумма ряда
. В этом случае сумма ряда  на интервале
на интервале  . Тогда если
. Тогда если 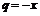 , то ряд
, то ряд . (3)
. (3) .
.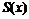 есть функция того же аргумента, что и члены ряда. В области сходимости
есть функция того же аргумента, что и члены ряда. В области сходимости 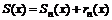 и
и 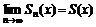 ,
,  . За ошибку вычислений принимают
. За ошибку вычислений принимают  .
. обозначим
обозначим  , то если для любых
, то если для любых  ряд
ряд  есть сходящийся числовой ряд. Т. е. существует предел
есть сходящийся числовой ряд. Т. е. существует предел  (или
(или  ). По определению предел последовательности означает, что
). По определению предел последовательности означает, что  существует натуральное число
существует натуральное число  такое, что для любых
такое, что для любых 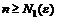 выполняется неравенство
выполняется неравенство  . Аналогично другая точка
. Аналогично другая точка  где ряд сходится. Т. е. существует предел
где ряд сходится. Т. е. существует предел  (или
(или  ). По определению предел последовательности означает, что
). По определению предел последовательности означает, что  такое, что для любых
такое, что для любых  выполняется неравенство
выполняется неравенство  .
. существует натуральное число
существует натуральное число 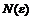 , не зависящее от
, не зависящее от  , такое, что для любых
, такое, что для любых  выполняется неравенство
выполняется неравенство  . Обозначается
. Обозначается 
 существует сходящийся знакоположительный числовой ряд
существует сходящийся знакоположительный числовой ряд  (5) для любых
(5) для любых  , то функциональный ряд сходится абсолютно и равномерно в области
, то функциональный ряд сходится абсолютно и равномерно в области  или
или  , для любых
, для любых  существует
существует  , откуда по определению 4 ряд сходится равномерно.
, откуда по определению 4 ряд сходится равномерно. . Область сходимости
. Область сходимости  . По признаку Вейерштрасса возьмем знакоположительный ряд
. По признаку Вейерштрасса возьмем знакоположительный ряд  . Данный ряд сходится (см. л. 45
. Данный ряд сходится (см. л. 45  ), причем
), причем  . Поэтому данный ряд правильно и равномерно сходится.
. Поэтому данный ряд правильно и равномерно сходится. . 3.
. 3.  .
.  .
. и члены ряда непрерывные функции, то и сумма ряда непрерывна на
и члены ряда непрерывные функции, то и сумма ряда непрерывна на 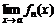 , то
, то  .
. .
. 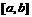 и члены ряда интегрируемы на
и члены ряда интегрируемы на  , то ряд (1) можно почленно интегрировать
, то ряд (1) можно почленно интегрировать  .
.  (6)
(6) , где
, где  – числа, коэффициенты ряда.
– числа, коэффициенты ряда.  , то получим ряд
, то получим ряд (7)
(7) . Если заменить
. Если заменить  , то можно перейти от (6) к (7). В точке
, то можно перейти от (6) к (7). В точке  ряд
ряд  сходится.
сходится. существует неотрицательное число R такое, что для любых
существует неотрицательное число R такое, что для любых  ряд абсолютно сходится, а для любых
ряд абсолютно сходится, а для любых 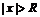 ряд расходится.
ряд расходится.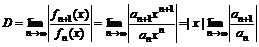 . Обозначим
. Обозначим  ,
,  . Тогда
. Тогда  . Ряд сходится если
. Ряд сходится если  или при
или при  –ряд (7) абсолютно сходится и при
–ряд (7) абсолютно сходится и при  (8)
(8) ряд (7) может сходиться или расходится. В этих точках необходимо исследовать ряд.
ряд (7) может сходиться или расходится. В этих точках необходимо исследовать ряд. Замечание!!!
Замечание!!! , то
, то  , а если
, а если  , то
, то  – с пропусками. Тогда
– с пропусками. Тогда  , откуда
, откуда  ;
;