
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дифференциальные уравнения высших порядков1. Зада Коши для ДУ высших порядков 2. ДУ высших порядков, допускающие понижение порядка 3. Линейные ДУ высших порядков 4. Линейные однородные ДУ второго порядка Цель занятия: Изучить понятие дифференциального уравнения высших порядков. Научиться классифицировать линейные однородные дифференциальные уравнения второго порядка и решать их. Роль и место лекции Для изучения данной лекции рекомендуется повторить материал предыдущих лекций, посвященный линейным ДУ и линейным однородным ДУ. Особую важность при изучении данной лекции, как и всей темы «Дифференциальные уравнения» играют знания методов интегрирования, таблицы производных и первообразных. Рекомендуется повторить вопрос однородности уравнения. Материал данной лекции необходим при решении прикладных задач, связанных с решением уравнений, в которые входят вторые производные, характеризующие скорость изменения скорости некоторого процесса. Вопрос № 1. Зада Коши для ДУ высших порядков Дифференциальные уравнения n-го порядка записываются в виде или Задача отыскания частного решения ДУ (2), удовлетворяющего начальным условиям Теорема № 1 (существования и единственности решения задачи Коши). Если в уравнении Вопрос № 2. ДУ высших порядков, допускающие понижение порядка  2.1. ДУ вида ДУ вида
ПРИМЕР № 1.
2.2. ДУ вида ДУ вида
называется неполным уравнением, не содержащим искомую функцию в явном виде. Решают такие уравнения с помощью подстановки
2.3. ДУ вида ДУ вида ПРИМЕР № 2. Решить Вопрос № 3. Линейные ДУ высших порядков Определение № 1. Дифференциальное уравнение высшего порядка, линейное относительно искомой функции и ее производных, называется линейным. Т. е. ДУ вида
где Если Частным случаем выражения (8) является ЛДУ 2-го порядка
Теорема № 2 (существования и единственности решения ЛНДУ 2П). Если функции Вопрос № 4. Линейные однородные ДУ второго порядка Как указывалось ранее, линейным однородным ДУ называется уравнение без правой части. Поэтому ЛОДУ 2П называется уравнение вида
Для удобства вводят оператор 4.1. Свойства ЛОДУ 2П. Свойство № 1. Если функции Доказательство. По условию
Свойство № 2. Если функции Свойство № 3. Если функции Вывод!!! Все решения ЛОДУ 2П образуют линейное пространство. 4.2. Определитель Вронского Определение № 2. Функции Замечание!!! Очевидно, что функции линейно зависимы тогда и только тогда, когда они пропорциональны, т. е. для всех Определение № 3. Определителем Вронского или Вронскианом двух функций называется определитель, составленный из функций и их первых производных
Теорема № 3. Для того чтобы две функции были линейно независимы на отрезке, необходимо и достаточно, чтобы
Теорема № 4 (о структуре общего решения ЛОДУ 2П). Если Доказательство. Вследствие свойств функция Определение № 4. Система двух линейно независимых решений ЛОДУ 2П называется фундаментальной системой, то есть остальные решения могут быть получены из их линейной комбинации. Заключение В заключении отметим, что отсутствие в однородном ДУ правой части, обусловлено свойством однородности функции (см. Л. 51). Данная лекция была посвящена вопросам решения линейных однородных ДУ второго порядка, однако приведенные рассуждения можно обобщить на случай ДУ n-го порядка по аналогии с решением систем уравнений с n-уравнениями. Так общим решение ЛОДУ n-го порядка будет - задача Коши справедлива для любого порядка ДУ; - только неполные ДУ высших порядков допускают снижение порядка; - при снижении порядка используют подстановку - общее решение ЛОДУ 2П состоит из двух линейно независимых решений; - в линейном однородном ДУ нет правой части Литература 21. Баврин И.И. Высшая математика. – М.: Просвещение, 2003. – 384 с. 22. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. – Ростов-на-Дону: Феникс, 1997. – 512 с. 23. Демидович Б.П., Кудрявцев В.А.Краткий курс высшей математики. – М.: Астрель, 2001. - 656 с. Лекция № 54 |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 175. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1)
(1) (2).
(2). ,
,  ,
,  ,…,
,…,  , называется задачей Коши ля ДУ n-го порядка.
, называется задачей Коши ля ДУ n-го порядка. непрерывна в области D, содержащей точку
непрерывна в области D, содержащей точку 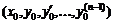 , а окрестности этой точки ограничена ее частная производная 1-го порядка по переменным
, а окрестности этой точки ограничена ее частная производная 1-го порядка по переменным 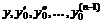 , то существует единственное решение ДУ, удовлетворяющая начальным условиям
, то существует единственное решение ДУ, удовлетворяющая начальным условиям  ,
,  ,
,  ,…,
,…, 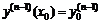 .
.
 (3) называется неполным уравнением, не содержащим искомую функцию и промежуточных производных. Очевидно, его общее решение находится путем n-кратного интегрирования. То есть
(3) называется неполным уравнением, не содержащим искомую функцию и промежуточных производных. Очевидно, его общее решение находится путем n-кратного интегрирования. То есть  , откуда
, откуда 


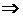
 . Аналогично
. Аналогично 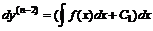
 и т. д. Таким образом общее решение будет иметь вид
и т. д. Таким образом общее решение будет иметь вид . (4)
. (4) ,
,  ,
, ,
, 

 (5)
(5) , где p – функция от x. Поскольку
, где p – функция от x. Поскольку  , то такая подстановка приведет (5) к ДУ 1-го порядка относительно p, т. е.
, то такая подстановка приведет (5) к ДУ 1-го порядка относительно p, т. е.  . Решая его, найдем эту функцию в некотором виде
. Решая его, найдем эту функцию в некотором виде  . Тогда с учетом подстановки
. Тогда с учетом подстановки  – ДУ 1-го порядка относительно y с разделяющимися переменными, откуда общее решение (5) будет иметь вид
– ДУ 1-го порядка относительно y с разделяющимися переменными, откуда общее решение (5) будет иметь вид (6).
(6).
 (7) называется неполным уравнением, не содержащим свободную переменную в явном виде. Решают такие уравнения с помощью подстановки
(7) называется неполным уравнением, не содержащим свободную переменную в явном виде. Решают такие уравнения с помощью подстановки  . Поскольку
. Поскольку  , то такая подстановка приведет (7) к ДУ 1-го порядка относительно p, т. е.
, то такая подстановка приведет (7) к ДУ 1-го порядка относительно p, т. е.  . Решая его, найдем функцию p в некотором виде
. Решая его, найдем функцию p в некотором виде  . Тогда с учетом подстановки
. Тогда с учетом подстановки  – ДУ 1-го порядка с разделяющимися переменными
– ДУ 1-го порядка с разделяющимися переменными  или
или  , откуда общее решение (7) будет иметь вид
, откуда общее решение (7) будет иметь вид  .
.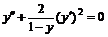 . Пусть
. Пусть  , тогда
, тогда  . Подставка дает
. Подставка дает  . Разделим переменные
. Разделим переменные  ,
,  . Тогда
. Тогда  ,
,  , откуда
, откуда 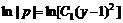 или
или  . С учетом подстановки
. С учетом подстановки  . Это ДУ 1-го порядка с разделяющимися переменными. Разделив переменные, получим
. Это ДУ 1-го порядка с разделяющимися переменными. Разделив переменные, получим  , проинтегрируем
, проинтегрируем  ,
,  , откуда
, откуда 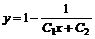 .
. , (8)
, (8) и
и  – заданные функции, y – искомая функция.
– заданные функции, y – искомая функция.  , то выражение (8) сводится (см. Л. 52) линейному дифференциальному уравнению без правой части или линейно однородному дифференциальному уравнению (ЛОДУ).
, то выражение (8) сводится (см. Л. 52) линейному дифференциальному уравнению без правой части или линейно однородному дифференциальному уравнению (ЛОДУ). . (9)
. (9) ,
, 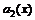 и
и 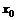 , то существует единственное решение (9), удовлетворяющее начальным условиям
, то существует единственное решение (9), удовлетворяющее начальным условиям  . (9)
. (9) . Поэтому выражение (9) может быть записано кратко
. Поэтому выражение (9) может быть записано кратко  .
.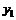 и
и  любые решения линейного однородного ДУ 2-го порядка, то
любые решения линейного однородного ДУ 2-го порядка, то  тоже решение этого уравнения.
тоже решение этого уравнения.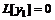 и
и  . Докажем, что
. Докажем, что  . С учетом (9)
. С учетом (9)  =
= 

 – решение линейного однородного ДУ 2-го порядка, а C – константа, то
– решение линейного однородного ДУ 2-го порядка, а C – константа, то  тоже решение этого уравнения.
тоже решение этого уравнения. и
и  константы, то
константы, то  тоже решение этого уравнения.
тоже решение этого уравнения.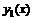 и
и  называются линейно независимыми на отрезке, если
называются линейно независимыми на отрезке, если  верно только при всех
верно только при всех  если это равенство выполняется хотя бы при одном
если это равенство выполняется хотя бы при одном  , то эти функции называются линейно зависимыми.
, то эти функции называются линейно зависимыми.  выполняется
выполняется 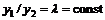 (см. линейную независимость векторов, часть 1).
(см. линейную независимость векторов, часть 1).
 в любой точке этого отрезка.
в любой точке этого отрезка. – произвольные константы, то
– произвольные константы, то  общее решение этого уравнения
общее решение этого уравнения ,
,  существуют единственные значения
существуют единственные значения  относительно
относительно  и
и  . Данная система из двух уравнений и двух неизвестных
. Данная система из двух уравнений и двух неизвестных  . Этот определитель есть Вронскиан двух функций
. Этот определитель есть Вронскиан двух функций  , а система имеет единственное решение. Вывод
, а система имеет единственное решение. Вывод  , где
, где  – линейно независимые решения ДУ. В следующей лекции будут рассмотрены методы нахождения этих решений. Отметим наиболее важное:
– линейно независимые решения ДУ. В следующей лекции будут рассмотрены методы нахождения этих решений. Отметим наиболее важное: или
или 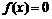 .
.