
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Формирование выражения для функции на основе таблицы истинности
Алгебраическое выражение для логической функции можно построить по таблице истинности, применяя КНФ (конъюнктивную нормальную форму) или ДНФ (дизъюнктивную нормальную форму). Формирование алгебраического выражения рассмотрим на примере таблицы истинности, представленной на Рис.
Формирование выражения для логической функции на основе КНФ: в таблице истинности рассматривать только строки, которые соответствуют значению функции «0»; для каждой такой строки записать дизъюнкцию из элементов строки; каждый элемент «а», имеющий значение «0», записать в дизъюнкции как «а», каждый элемент «b», имеющий значение «1», инвертировать, т.е. записать как « F1(a,b,c) = (a+b+c)(a+
Формирование выражения для логической функции на основе ДНФ: в таблице истинности рассматривать только строки, которые соответствуют значению функции 1; для каждой такой строки записать конъюнкцию из элементов строки; каждый элемент «а», имеющий значение «1», записать в конъюнкции как «а», каждый элемент «b», имеющий значение «0», инвертировать, т.е. записать как « F2(a,b,c) =
Построим для каждой функции F1 и F2 таблицы истинности и покажем, что эти выражения равносильны, т.е. имеют одинаковые значения для одинаковых комбинаций значений аргументов.

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
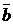 »; полученные дизъюнкции объединить конъюнкциями.
»; полученные дизъюнкции объединить конъюнкциями. 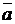 +b+c)(
+b+c)( 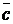 )
)