
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Эквивалентность (равнозначность)
Два высказывания эквивалентны (равнозначны), когда их значения истинности одинаковы. Например, эквивалентны высказывания: "железо тяжелое" и "пух легкий" или высказывания: "железо легкое" и "пух тяжелый". Обозначим эквивалентность символом «↔» и запись "a ↔ b" будем читать "a эквивалентно b". Эквивалентность (равнозначность): сложное высказывание, состоящее из двух простых высказываний – a и b, которое истинно тогда, когда оба высказывания a и b истинны, или когда оба высказывания a и b ложны.
Словесно функция равнозначности формулируется следующим образом: «a тогда и только тогда, когда b». Высказывание типа «a тогда и только тогда, когда b» можно заменить высказыванием «если a, то b и, если b, то a» (отсюда видна причина, по которой использована двунаправленная стрелка «↔» для обозначения этой функции). Следовательно, функцию «эквивалентность» можно заменить комбинацией функций импликации и конъюнкции: a ↔ b = (a → b) & (b → a) или a ↔ b = (a → b)(b → a). Пример. Число S делится на 3 тогда и только тогда, когда сумма цифр числа S делится на 3. a = «Число S делится на 3». b = «Сумма цифр числа S делится на 3». a ↔ b Пример. Даны простые высказывания: а = «Принтер – устройство вывода информации». b = «Процессор – устройство хранения информации». с = «Монитор – устройство вывода информации». d = «Клавиатура – устройство обработки информации». Определить значение составного высказывания: (a& b) & (c V d) = ab(c+d) = ?  Определим на основе знания компьютера истинность простых высказываний: a=1; b=0; c=1; d=0. Значение составного высказывания: = ab(c+d) = 1&0&(1+0) = 1&0&1=0 Формы логических функций Существуют базовые логические функции: отрицание, конъюнкция, дизъюнкция. Элементарная конъюнкция: конъюнкция, состоящая только из различных аргументов и отрицаний (в элементарной конъюнкции не должен присутствовать аргумент и его же отрицание). Элементарные конъюнкции: ab; a Элементарная дизъюнкция: дизъюнкция, состоящая только из различных аргументов и их отрицаний (в элементарной дизъюнкции не должен присутствовать аргумент и его же отрицание). Элементарные дизъюнкции: a+b; a+ Алгебраические выражения могут упрощаться с использованием различных формул (например, x2+2xy+y2= (x+y)2; x2-y2=(x+y)(x-y) и т.д.) вынесением общих элементов за скобки (например, x3+2x2y+xy2=x(x2+2xy+y2) и т.д.) до такой записи, когда невозможно упростить выражение. Аналогичная ситуация существует в алгебре логики – логических выражениях. Более того, в алгебре логики существуют «стандарты», которые определяют форму выражения, при которой выражение невозможно упростить. Такие стандарты описывают выражения алгебры логики, которые называются «форма». Дизъюнктивная нормальная форма (ДНФ): выражение, в котором элементарные конъюнкции и одиночные аргументы соединяются между собой дизъюнкциями. Дизъюнктивная нормальная форма: Конъюнктивная нормальная форма (КНФ): выражение, в котором элементарные дизъюнкции и одиночные аргументы соединяются между собой конъюнкциями. Конъюнктивная нормальная форма: (
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 891. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||
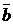 ; ab
; ab 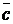 .
.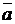 b+ a
b+ a