Логические переменные, логические операции, логические функции

Логическая переменная: переменная, которая может принимать только одно из двух значений: «истина», «ложь».

Простое высказывание трактуется в булевой алгебре, как логическая переменная.

Примеры.

Логическая переменная А = «Дважды два равно 4».

Логическая переменная В = «Дважды два равно 5».

Функция: закон соответствия между переменными.

Логическая функция: закон соответствия между логическими переменными.

Логическая функция (логическое выражение): символическая запись, состоящая из логических величин (констант или переменных), объединенных логическими операциями (связками).

Сложное (составное) высказывание состоит из простых высказываний, соединённых логическими операциями.

Логическая функция, как и логическая переменная,  может принимать только одно из двух значений: «истина», «ложь».

В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, а сложным высказываниям – логические функции. Обозначаются логические переменные и логические функции буквами латинского алфавита.

Существуют разные варианты обозначения значений логических переменных и функций:

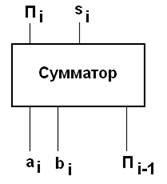
Будем использовать один вариант обозначений: 0, 1. В этом случае можно говорить, что логические переменные и логические функции определены на множестве {0,1}.

Арифметические выражения, как правило, определены на большом интервале значений аргументов. Иная ситуация с логическими выражениями – функциями. И логические аргументы, и логические функции определены только на множестве {0, 1}. По этой причине для каждой функции определяется соответствие между значениями аргументов и значениями функции.

Таблица истинности функции: таблица, устанавливающая соответствие между возможными наборами значений аргументов (логических переменных) и значениями функции.

Пример.  На рис. представлено устройство,  имеющее 3 логические переменные и 2 логические функции.

Таблица истинности функций s_i и П_i+1:

Из таблицы истинности можно видеть, что в ней представлена логика функционирования устройства «сумматор», которое выполняет суммирование содержимого одного разряда i двух чисел с учётом переноса, который может возникнуть при суммировании содержимого предыдущего i-1 разряда.

Пример. Суммирование двух чисел: А и В.

Из таблицы можно видеть следующее. В разряде «0» отсутствует перенос из предыдущего разряда и в последующий разряд. В разрядах «1» и «3» отсутствует перенос из предыдущего разряда, и возник перенос в последующий разряд. В разрядах «4» и «5» имеется перенос из предыдущего разряда, и возник перенос в последующий разряд.

Сопоставьте суммирование в этих разрядах с таблицей истинности сумматора.

Представление высказываний в виде логических выражений

Логические функции:

1.отрицание (инверсия);

2.логическое умножение (конъюнкция);

3.логическое сложение (дизъюнкция).

4.логическое следование (импликация);

5. эквивалентность (равнозначность);

Функции 1-3 называются базовыми. Такое название эта группа функций получила по той причине, что функции 4-5 и другие функции с собственными именами (которые мы не рассматриваем), а также всё множество сложных логических функций выражаются через базовые функции.