
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Построение таблиц истинности для логических функцийТаблица истинности была определена в п.1. Определим её ещё раз. Таблица истинности функции: таблица, устанавливающая соответствие между возможными наборами значений аргументов (логических переменных) и значениями функции. Все столбцы таблицы истинности можно сгруппировать в 3 части. В первой части каждый столбец соответствует имени аргумента (логической переменной). Во второй части каждый столбец соответствует результату выполнения одной логической операции. Столбцы во второй части необходимо располагать «слева-направо» с учётом приоритета выполнения операций. Третья часть состоит из одного столбца – значений функции для различных комбинаций аргументов. Количество строк в таблице истинности равно количеству комбинаций значений аргументов. Каждый аргумент имеет только 2 значения: 0 и 1. По этой причине количество m комбинаций значений аргументов для n аргументов равно m = 2n. Каждую комбинацию значений аргументов удобно представлять в виде числа в системе счисления с основанием р=2, начиная с 0 и кончая числом m-1. В таблице на Рис. Представлена таблица со всеми комбинациями значений для 3-х аргументов: a, b, c.
Т.к. все логические функции представляют собой соединение логических переменных с помощью базовых операций (функций), необходимо, как и для арифметических операций, определить порядок выполнения логических операций, т.е. определить их приоритеты (старшинство). 
В этой таблице показано, что при записи без скобок последовательности логических операций, в первую очередь выполняются операции «отрицание», во вторую очередь – операции «логическое умножение», в третью – операции «логическое сложение» и в четвёртую очередь – операции «импликация» и «эквивалентность». Последние 2 операции имеют равный приоритет, и выполняются в порядке записи в выражении. Для изменения естественного порядка выполнения логических операций используются круглые скобки. Пример. Построить таблицу истинности для функции F(a,b)= (a \/ b).
Пример. Построить таблицу истинности для логической функции: F(a,b,c)=b↔(a+c).
В данной таблице истинности столбцы первой части разделены столбцом со значениями функции (a+c), имеющейся в выражении. Это сделано для удобства определения значений этой функции.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 538. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
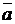 )
)