
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Линейные разностные уравнения с постоянным коэффициентом.Ких и Бих системы. Аналоговые системы во временной области описываются системой дифференциальных уравнений. Для цифровых систем аналогами дифференциальных уравнений являются разностные уравнения, те есть дискретные системы описываются разными уравнениями.При последовательности x(n) и начальных условиях разностные уравнения однозначно определяют y(n). Пример:
Особую роль играет класс ЛДС, для которых вход и выход удовлетворяет линейное разностное уравнение «n» порядка.
аkи bj – постоянные коэффициенты. Выразим выход системы:
Согласно этому уравнению выходные значения определяются через n значений выхода и m значений входа. ЛДС может иметь импульсную характеристику h(n) как конечной, так и бесконечной длины. Соответственно ЛДС называют системой с конечной импульсной характеристикой и бесконечной импульсной характеристикой . Ких система может быть описана частным видом (2) при n=0. В этом случае значение выход полностью определяет M+1 значений входа и уравнение (2) превращается в уравнение (1).
В отличии от Ких систем, у Бих система n>0. Описание ЛДС и дискретных сигналов в частотных системах. Z-преобразования. Передаточная функция и частотная характеристика. Для решения дифференциальных уравнений, описывающих аналоговые системы, используют преобразования Лапласа. В результате получается алгебраическое уравнение. Наиболее подходящим методом решения уравнений является z-преобразования, то есть дискретный аналог преобразований Лапласа. x(z)
Где z- комплексная переменная, x(z)- комплексная функция.  x(z) определена для тех значений zи z-1, для которых (4) сходится.
По условиям сходимости x(z)определена для тех значений z с радиусом r в z-плоскости, для которых:
Пример:
На рисунке показана область определения. Свойства z-преобразований. · Свойство однозначности. Каждой x(z) соответствует одно x(n):
· Линейность. z- преобразования-это линейный оператор.
· Свойство сдвига
· Свойство свертки
Y(z)=x1(z)x2(z). Передаточная функция ЛДС. Применяя свойство к (2) к обеим частям:
H(z)- передаточная функция системы, отношение z-преобразований выхода к z- преобразований входа. Она полностью описывает ЛДС частотной области. Частотная характеристика. Другой важной характеристикой ЛДС является частотная характеристика системы. Частотная характеристика- Фурье изображение или преобразование Фурье импульсной характеристики h(n).
Комплексная функция
Где Свойства частотной характеристики: 1. Частотная характеристика и ее составляющие- непрерывные функции частоты 2. АЧХ и ФХЧ- периодические функции, с периодом равным
3. Модуль АЧХ- четная функция, а модуль ФЧХ- нечетная функция. Понятие ЧХ применимо как для ЛДС так и к самим сигналам на входе и выходе системы.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 259. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
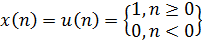





 (2)
(2)
 x(n) определяется следующим образом:
x(n) определяется следующим образом: (3)
(3)

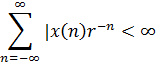
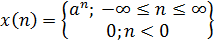

 , следовательно ряд сходится.
, следовательно ряд сходится.


 , тогда, когда
, тогда, когда


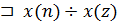 , то
, то zk
zk




 - частотная характеристика.
- частотная характеристика.
 можно представить в виде:
можно представить в виде:
 .
. .
.
