
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Следовательно, гипотеза о равенстве дисперсий отвергается.Необходимо проверить гипотезу о близости нашего ряда распределения нормальному закону. Если такое соответствие удастся установить, то этим выявиться случайный характер результатов измерения. Первоначально выполним приближенную проверку гипотезы с помощью асимметрии А и эксцесса Е. Полученные величины сравниваем со значениями средних квадратических отклонений этих величин, вычисленных по формулам:
Величины:
В нашем случае выполняются следующие условия:
Вывод: гипотезу о соответствии эмпирического распределения нормальному нельзя считать противоречащей результатам наблюдений. При большом числе измерений и группировании данных пользуются для проверки гипотезы о нормальном законе распределения критериями согласия Колмогорова и В первом случае необходимо установить теоретическую функцию F(x) и ее расхождение с эмпирической Fn(x). Вычисления выполнены в таблице 5.
Таблица 5
При вычислении функции Ф(t) параметр t определяется по формуле: 
Где а=21,4635; σ =0,005
Согласно табл.5 наибольшее расхождение
Значение 1-К( Этому значению соответствует Вывод: гипотеза о нормальности распределения противоречит результатам наблюдений. Проверим нашу гипотезу с помощью критерия Таблица 6
Полученное значение
Вывод: расхождение между теоретическим и эмпирическим распределениями следует считать не случайными, и гипотеза о нормальности распределения противоречит результатам измерений.
Литература: 1. Большаков В.Д. Теория ошибок наблюдений: Учебник для вузов.-М.Недра,1983. 2. Методические указания по «Теории математической обработки геодезических измерений» - А.Р.Губеладзе, Е.Н. Яговкина, Л.Ф. Литвинова - 2002. 3. Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений.-М.Недра,1984. 4. Смирнов Н.В., Белугин Д.А. Теория вероятностей и математическая статистика в приложении геодезии.-М.: Недра, 1969..
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
КАФЕДРА ПРИКЛАДНОЙ ГЕОДЕЗИИ
КУРСОВАЯ РАБОТА
Обработка результатов эксперимента
Выполнил студ. гр. ПГ-291 Петров Р.А. Проверил преподаватель Яговкина Е.Н.
Ростов-на-Дону 2010
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 349. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 м
м м
м м
м м
м ;
;  .
. . Для нашего примера используем оба этих метода.
. Для нашего примера используем оба этих метода.

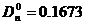 , тогда значение
, тогда значение 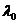 оказалось равным:
оказалось равным: =1,86
=1,86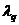 , которая определяется по значению К(
, которая определяется по значению К(  )=1-0,002=0,998
)=1-0,002=0,998 и выравнивающие
и выравнивающие 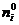 частоты. Выравнивающие частоты определяются по вероятности попадания случайной величины в заданный интервал и объему выборки n, т.е.
частоты. Выравнивающие частоты определяются по вероятности попадания случайной величины в заданный интервал и объему выборки n, т.е. 

 , которое находится по степеням свободы К = r – 3 = 11 – 3 = 8 и заданному уровню значимости q=0.06. Выполняется следующее условие:
, которое находится по степеням свободы К = r – 3 = 11 – 3 = 8 и заданному уровню значимости q=0.06. Выполняется следующее условие: