
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основные положения по анализу точности.Стр 1 из 5Следующая ⇒ Введение Важнейшей характеристикой современного строительства являются качество изготовления конструкций, их установка и монтаж. Большую роль играет соблюдение проектных размеров как всего сооружения в целом, так и отдельных его элементов. Но размеры конструкций и сооружения после их изготовления и монтажа могут в значительной степени отличаться от проектных. Отклонение действительных параметров может быть как положительным (в сторону увеличения), так и отрицательным (в сторону уменьшения). Отсюда следует, что все размеры имеют свои предельные значения: наибольший xmax и наименьший xmin (рис.1). На рис.1. рассматривается в качестве объекта рельсовый путь мостового полярного крана. Разность между экстремальными значениями составляют допустимую величину положения объекта δ, т.е. δ= xmax- xmin (1) Необходимо подразделить все размеры и допуски на конструкционные и производственные. К конструкционным относятся те, которые удовлетворяют оптимальным эксплуатационным требованиям, предъявляемым к сооружениям. К производственным допускам относятся такие, которые необходимо соблюдать в процессе изготовления конструкций, при выполнении строительно-монтажных работ. Необходимо, чтобы эти допуски соответствовали всем требованиям, предъявляемым проектом к качеству сооружения. Все допуски устанавливаются исходя из расчета точности конструкций. Установленная проектом точность определяется допуском, а полученная точность оценивается ошибками, возникшими при производстве строительно-монтажных работ, и в процессе производства геодезических измерений. 
X
Рис.1. Применение геодезических методов ставит ряд задач, которые необходимо решать на различных этапах. На предварительном этапе, включающем в себя предварительную оценку состояния объекта, и всех последующих, заключающихся в проведении работ по определению полной геометрии сооружения с учетом его напряжно-деформационных нагрузок, необходимо установить достаточную точность геодезических измерений. В дальнейшем появляются вопросы, связанные с устранением отклонений параметров объекта от номинальных. В таких случаях требуется особый подход к оценке как самого состояния сооружения, так и к точности геодезических работ, при этом их можно увязать друг с другом, т.е. техническое состояние влияет на производство геодезических работ и точность геодезических измерений, что позволяет оценить состояние объекта.
Основные положения по анализу точности. Точность и допуски необходимо рассматривать как качественную оценку, характеризующую конструкции, сооружения в целом, подготовительные работы, строительство и монтаж. При этом система допусков представляет собой стандартизацию точности технологических процессов при возведении сооружения, опирающуюся на предельные ошибки. Исходя из вероятностного подхода к теории ошибок измерений было установлено, что случайные ошибки результатов измерений подчиняются нормальному закону распределения. Знание функции плотности распределения таких ошибок дает возможность для решения целого ряда задач, возникающих в ходе геодезических работ: 1)определение наиболее вероятного значения измеряемой величины; 2)установление предельных значений (допусков) для конкретно вида работ; 3)вычисление вероятности появления случайной ошибки в определенном интервале; 4)выявление предельных значений, после которых ошибки можно квалифицировать как грубые. Для этого воспользуемся функцией Лапласа, имеющей следующий вид: Где t- нормированный параметр функции Лапласа. Вероятность того, что случайная величина х примет значение, принадлежащее интервалу (α;β), можно выразить через функцию распределения: Р(α<x<β)=F(β)-F(α). (3) Переходя к нормированной случайной величине t, имеем: Р( tα < t < t β ) = Ф(tβ )-Ф( t α) (4) где tα = а-математическое ожидание случайной величины; σ-среднее квадратическое отклонение случайной величины. Определим вероятность того, что нормально распределенная величина х отклоняется от своего математического ожидания на величину, меньшую чем ε , т.е. найдем вероятность осуществления неравенства: a - ε < x < a+ ε. Так как t=ε/σ, то: Р( tα < t < t β )=Ф Окончательно имеем: Р(/ х – а / < ε )=Ф Или Р(/ х – а / < tσ )=Ф(t). (7) Таким образом, значение Ф(t) при заданном t определяет вероятность того, что отклонение нормально распределенной величины по абсолютному значению меньше tσ. Доверительная вероятность: Р( / х – а / < σ )=Ф(1)=0,6827 при t= 1; Р( / х – а / < 2σ )=Ф(2)=0,9545 при t= 2; Р( / х – а / < 3σ )=Ф(3)=0,9973 при t= 3. Из последнего равенства следует, что практически рассеивание случайной величины укладыватся на участке М ± 3σ. Можно считать, что предельным значением ошибки является величина 3σ , а в качестве допуска – ее удвоенное значение, т.е. δ= 6 σ .
|
|||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 349. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Границы максимальных отклонений
Границы максимальных отклонений





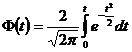 (2)
(2)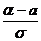 ; t β=
; t β= 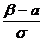 ;
; . (5)
. (5)