
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Вычисление эмпирических характеристик распределения.
Практически при многократных измерениях полученные результаты х1,х2,…,хn группируют по классам (интервалам), определяя частоту n1,n2,…,nk появления этих результатов в соответствующем классе и вычисляя эмпирические (приближенные) значения вероятностей – частости: где j=1,2,…,k и Применение систем классов необходимо при обработке больших рядов распределения случайной величины. Для определения шага интервала используют формулу Г. Стерджесса: где xmax , xmin - соответственно максимальное и минимальное значения случайной величины; n – число наблюдени. Вычисляют накопленные частоты согласно Nj=n1+n2+…+nj. (23) Затем определяют накопленную частость или эмпирическую функцию распределения Fn(x) Fn(x)=
Рис. 3 Для решения поставленной задачи необходимо подвергнуть данный ряд распределения статистическому анализу. При этом определяют эмпирические числовые характеристики распределения: математическое ожидание, дисперсию, среднее квадратическое отклонение, асимметрию и эксцесс. В дальнейшем проводится оценка точности параметров распределения. Для выявления случайного характера распределения значений горизонтального угла проверяется гипотеза близости данного ряда нормальному закону распределения.  Для проведения группирования сначала нужно установить шаг интервала:
Установим шаг и границы интервалов, вычисляем частоты, частоты и величину накопленной частости. Результаты вычислений представлены в табл.1. Таблица 1
165 1.000 По результатам табл.1. построим графики: полигон, гистограмму и график накопленной частости или функции эмпирического распределения.(рис.4,рис.5,рис.6)
Рис 4. Полигон частот
Рис 5. Гистограмма частот
Рис 6. График накопленной частости
При большом объеме выборки для определения эмпирических параметров распределения предварительно вычислим относительные начальные моменты. Вычисление относительных начальных моментов выполнено в табл.2.
Таблица 2
Вычислим вероятнейшее значение угла: Xср1=Δx*ν1+c=0.02*0.03+21.460=21.4606 м
Проведем группирование на интервале от 21.4500 до 21.4720. Для этого установим шаг интервала:
Установим шаг и границы интервалов, вычисляем частоты, частоты и величину накопленной частости. Результаты вычислений представлены в табл.3. Таблица 3
123 1.000 По результатам табл.3. построим графики: полигон, гистограмму и график накопленной частости или функции эмпирического распределения.(рис.7,рис.8,рис.9)
Рис 7. Полигон частот
Рис 8. Гистограмма частот
Рис 9. График накопленной частости При большом объеме выборки для определения эмпирических параметров распределения предварительно вычислим относительные начальные моменты. Вычисление относительных начальных моментов выполнено в табл.4. Таблица 4
Вычислим вероятнейшее значение угла:
Xср2=Δx*ν1+c=0.0020*0.27+21.4600=21.4635 м
Для вычисления эмпирических значений дисперсий, асимметрии и эксцесса воспользуемся центральными моментами, которые находятся через начальные по формулам:
-3*0,00531441)=0.0000000014 м
Имеем:
Откуда среднее квадратическое отклонение составит:
Произведем интервальную оценку математического ожидания MX=a. Учитывая большой объем выборки, можно принять
21.4635-1.88
21.4635-0.0008476 < a < 21.4635+0.008476 21.4626 < a < 21.4643 Для интервальной оценки дисперсии
Т.к. число степеней свободы больше 30, то соответствующее значение
В нашем случае значение
а величина
Затем определяем доверительный интервал для дисперсии:
0.000020 <
Соответственно для стандарта или среднего квадратического отклонения интервал составит:
0.0045 <
В дальнейшем необходимо проверить гипотезы о параметрах распределения. В этом случае произвольно берутся эмпирические значения параметров распределения: среднее арифметическое и эмпирическая дисперсия Xср2=21,4635 и При большом объеме выборки можно считать, что
Параметр t при доверительной вероятности P=0.94 равен 1,88. Тогда величина Выдвигается гипотеза о равенстве дисперсий
F=
Полученное значение F сравниваем с табличным, взятым по степеням свободы к
F=7.60 > Fq=1.54
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 459. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 (20)
(20) (21)
(21) (22)
(22) (24)
(24)
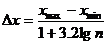
 м
м




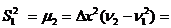 0.0004*(0.49-0.009)=0.00019 м
0.0004*(0.49-0.009)=0.00019 м м
м


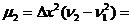 0.0004*(6.33-0.0729)=0.000025 м
0.0004*(6.33-0.0729)=0.000025 м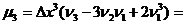 0,000008*(0.619-3*6.33*0.27+2*0,019683)=-0,000000036 м
0,000008*(0.619-3*6.33*0.27+2*0,019683)=-0,000000036 м 0,00000016*(84.87+4*0.61*0.27+6*6.33*0.27-
0,00000016*(84.87+4*0.61*0.27+6*6.33*0.27-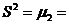 0,000025 м
0,000025 м м
м Параметр t по функции Ф(t)=0.94 согласно таблице равен 1,88. Тогда доверительный интервал определиться как:
Параметр t по функции Ф(t)=0.94 согласно таблице равен 1,88. Тогда доверительный интервал определиться как: < a < 21.4635+1.88
< a < 21.4635+1.88  воспользуемся зависимостью:
воспользуемся зависимостью:
 определяется из выражения:
определяется из выражения: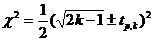
 получится равным:
получится равным: =93,9609 м,
=93,9609 м, соответственно:
соответственно: =152,5735 м
=152,5735 м
 < 0.000033
< 0.000033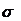 < 0.0057
< 0.0057 =0,000025. Проверить нулевую гипотезу о равенстве центров распределения.
=0,000025. Проверить нулевую гипотезу о равенстве центров распределения. . Разность средних значений составит
. Разность средних значений составит  . Ее сравнивают с величиной
. Ее сравнивают с величиной 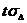 , где параметр t находится из приложения, а
, где параметр t находится из приложения, а  вычисляется по формуле:
вычисляется по формуле: м
м >
>  . Используем значение F-распределения согласно формуле:
. Используем значение F-распределения согласно формуле:
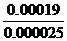 =7.60 м
=7.60 м =122 и к
=122 и к  =164 при доверительной вероятности P=0.94 и уровню значимости q=0.06 (Fq=1.54).
=164 при доверительной вероятности P=0.94 и уровню значимости q=0.06 (Fq=1.54).