
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
В частном случае наложения двух полей
а модуль магнитной индукции
где a – угол между векторами В случае непрерывного проводника принцип суперпозиции выглядит так:
Здесь интеграл берётся по всему проводнику. Индукция, созданная непрерывным проводником с током, равна интегралу от элементарных индукций полей, созданных каждым элементом тока в отдельности. · Закон Ампера. Сила Ампера, действующая на элемент тока
Здесь · Индукция магнитного поля прямолинейного проводника с током I бесконечной длины на расстоянии r от проводника:
· Индукция магнитного поля в центре кругового витка с током I:
и направлена по правилу правого винта (рис. 4.6). Здесь R – радиус витка. · Индукция магнитного поля на оси кругового витка радиусомRс током Iна расстоянии h от центра витка:
· Индукция магнитного поля, создаваемого отрезком прямого проводника (см. обозначения на рис. 4.7):
Вектор индукции
· Индукция магнитного поля на оси соленоида в произвольной точке А (рис. 4.8):
 · Индукция на оси бесконечно длинного соленоида:
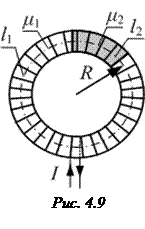
· Индукциямагнитного поля тороида, сердечник которого составлен из двух частей, изготовленных из веществ с различными магнитными проницаемостями, на осевой линии тороида (рис. 4.9):
где I – сила тока в обмотке тороида; N – число её витков; l1 и l2 – длины первой и второй частей сердечника тороида по осевой линии; m1 и m2 – магнитные проницаемости веществ первой и второй частей сердечника тороида; m0 –магнитная постоянная. · Индукциямагнитного поля, созданного движущимся со скоростью
· Потенциальная (механическая) энергия контура с током в магнитном поле
Здесь · Сила, действующая на рамку с током в неоднородном магнитном поле.Проекция силы на произвольную ось OX равна
где · Сила Лоренца (сила, действующая на заряд q, движущийся со скоростью
где · Циркуляция вектора магнитной индукции вдоль замкнутого контураL –это интеграл по замкнутому контуру L:
где · Циркуляция вектора напряжённости
Здесь · Закон полного тока(теорема о циркуляции): циркуляция вектора магнитной индукции
Для индукции поля в магнетике:
Суммирование производится по всем токам, охваченным контуром: и макротокам (токам проводимости), и микротокам. Циркуляцию вектора магнитной индукции также можно записать через сумму только токов проводимости:
Здесь m – магнитная проницаемость магнетика; n – число макротоков; k – число микротоков. · Циркуляция напряжённости
где
причём интегрирование ведётся во всей поверхности S. · Работа по перемещению замкнутого контура с током в магнитном поле dA=I∙dФ, или A=I∙DФ, где DФ – изменение магнитного потока, пронизывающего поверхность, ограниченную контуром; I – сила тока в контуре. · Потокосцепление, то есть полный магнитный поток, сцепленный со всеми N витками соленоида или тороида:
где · Закон Фарадея (закон электромагнитной индукции): ЭДС индукции , точнее, Если контур содержит N витков, то
где Среднее значение ЭДС индукции:
· Частные случаи применения закона Фарадея:
U=B∙l∙u∙sina, где a – угол между направлениями векторов скорости б) электродвижущая сила индукции
где · Индуктивность контураLчисленно равна магнитному потоку Ф, пронизывающему контур, при единичной силе тока в контуре:
Для катушки (соленоида, тороида) с N витками
где · Индуктивность соленоида (тороида):
где N – число витков, l – длина соленоида, S – площадь сечения соленоида, · ЭДС самоиндукции
Среднее значение ЭДС самоиндукции · Заряд, прошедший через поперечное сечение проводника в замкнутом контуре при возникновении в нём индукционного тока при изменения магнитного потока:
где R – сопротивление контура; · Энергия магнитного поля, создаваемого током в замкнутом контуре:
Здесь I – сила тока в контуре, L – его индуктивность,
· Объёмная плотность энергии магнитного поля (энергия единицы объёма;
где
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 605. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 ,
, и
и  .
.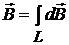 .
. , находящийся в магнитном поле
, находящийся в магнитном поле  :
: , или
, или  .
. – угол между направлением элемента тока
– угол между направлением элемента тока  ,
, где
где  – магнитная постоянная, μ – магнитная проницаемость среды (для вакуума μ=1). Направление тока и магнитной индукции связаны правилом буравчика (рис. 4.5).
– магнитная постоянная, μ – магнитная проницаемость среды (для вакуума μ=1). Направление тока и магнитной индукции связаны правилом буравчика (рис. 4.5).
 .
.
 .
. .
. ,
, где
где  – плотность намотки соленоида (число витков на единицу длины; N – полное число витков соленоида длиной l); углы α1 и α2 – см. рис. 4.8.
– плотность намотки соленоида (число витков на единицу длины; N – полное число витков соленоида длиной l); углы α1 и α2 – см. рис. 4.8.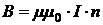 .
.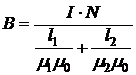 ,
, зарядом q в точке с радиус-вектором
зарядом q в точке с радиус-вектором  (рис. 4.10):
(рис. 4.10): ; или
; или  .
. · Сила взаимодействия двух параллельных бесконечных проводников с токами I1 и I2, находящимися на расстоянии r, рассчитанная на отрезок проводника длиной l:
· Сила взаимодействия двух параллельных бесконечных проводников с токами I1 и I2, находящимися на расстоянии r, рассчитанная на отрезок проводника длиной l: .
. .
. контура с током и вектором
контура с током и вектором  ,
, – быстрота изменения поля вдоль оси OX,
– быстрота изменения поля вдоль оси OX,  в магнитном поле с индукцией
в магнитном поле с индукцией  ):
): , или
, или  ,
,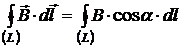 , или
, или  ,
, – проекция вектора
– проекция вектора  контура.
контура. магнитного поля вдоль замкнутого контура L:
магнитного поля вдоль замкнутого контура L: , или
, или 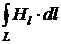 .
. – проекция вектора
– проекция вектора 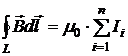 .
. .
.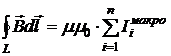 .
. .
. · Магнитный поток (поток вектора магнитной индукции
· Магнитный поток (поток вектора магнитной индукции  , или
, или  ,
, к поверхности (рис. 4.11);
к поверхности (рис. 4.11);  – проекция вектора
– проекция вектора 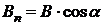 ). В случае неоднородного поля:
). В случае неоднородного поля: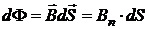 ;
;  ,
, ,
,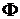 – магнитный поток через один виток.
– магнитный поток через один виток. в замкнутом контуре равна по величине и противоположна по знаку скорости изменения полного магнитного потока через поверхность, ограниченную контуром:
в замкнутом контуре равна по величине и противоположна по знаку скорости изменения полного магнитного потока через поверхность, ограниченную контуром: .
. , или
, или  ,
, (один виток);
(один виток);  (N витков).
(N витков).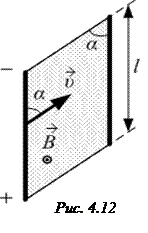 а) разность потенциалов U на концах проводника длиной l, движущегося со скоростью u в однородном магнитном поле индукцией B (рис. 4.12):
а) разность потенциалов U на концах проводника длиной l, движущегося со скоростью u в однородном магнитном поле индукцией B (рис. 4.12): ,
,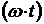 – мгновенное значение угла между вектором
– мгновенное значение угла между вектором  к плоскости рамки.
к плоскости рамки. .
. ,
, , или
, или  ,
,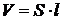 – его объём,
– его объём,  – плотность намотки соленоида.
– плотность намотки соленоида. , возникающая в катушке с индуктивностью L, при изменении силы тока в ней:
, возникающая в катушке с индуктивностью L, при изменении силы тока в ней: .
. .
.
 – изменение потокосцепления.
– изменение потокосцепления. , или
, или  , или
, или  .
. – полное потокосцепление, N – число витков. В случае
– полное потокосцепление, N – число витков. В случае  :
: .
.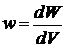 ):
): , или
, или  , или
, или 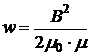 ,
,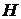 – напряжённость магнитного поля,
– напряжённость магнитного поля,  – магнитная индукция, m – магнитная проницаемость;
– магнитная индукция, m – магнитная проницаемость;  – магнитная постоянная.
– магнитная постоянная.