
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Моменты инерции некоторых тел правильной геометрической формы
· Теорема Штейнера: момент инерции тела относительно произвольной оси равен:
где · Момент импульса вращающегося тела относительно оси:
где · Закон сохранения момента импульса. Если суммарный момент внешних сил, действующих на систему, равен нулю, то полный момент импульса системы сохраняется: Если или где Li – момент импульса i-го тела, входящего в состав системы, N – число тел в системе. Для двух взаимодействующих тел замкнутой системы:
где  · Закон сохранения момента импульса для одного тела, момент инерции которого меняется:
где · Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси (второй закон Ньютона для вращательного движения): угловое ускорение
· Второй закон Ньютона для вращательного движения в импульсной форме (закон изменения момента импульса тела): изменение момента импульса тела
Если момент сил, действующих на тело, постоянен, то
где · Работа момента силы
Если момент сил постоянен (
Здесь · Мгновенная мощность, развиваемая при вращении тела:
· Кинетическая энергия вращающегося тела:
· Кинетическая энергия тела, катящегося по плоскости без скольжения:
где Механические колебания · Кинематическое уравнение гармонических колебаний
Здесь х –смещение колеблющейся точки из положения равновесия; t – время; А –амплитуда колебаний; ω – круговая (циклическая) частота колебаний;
· Круговая (циклическая) частота колебаний:
где · Скорость точки, совершающей гармонические колебания:
· Ускорение колеблющейся точки при гармонических колебаниях:
· Период колебаний пружинного маятника (тела массой m, подвешенного на пружине жёсткостью k, рис. 1.16):
Формула справедлива для малых колебаний, пока выполняется закон Гука · Период колебаний математического маятника (материальной точки массой m, подвешенной на нерастяжимой невесомой нити длиной l, рис. 1.17):
где g –ускорение свободного падения. · Период колебаний физического маятника (твёрдого тела, подвешенного в поле силы тяжести и способного колебаться относительно оси, не проходящей через центр масс, рис. 1.18):
Здесь J – момент инерции колеблющегося тела относительно оси колебаний, l – расстояние от центра масс маятника до оси (длина физического маятника),
Формулы для периода колебаний физического и математического маятников справедливы при малых углах отклонения, когда можно положить  . Для α=150 ошибка в значении периода не превышает 1 %, а при α=30 ошибка равна 0.005 %. . Для α=150 ошибка в значении периода не превышает 1 %, а при α=30 ошибка равна 0.005 %.
· Период колебаний крутильного маятника (тела, подвешенного на упругой нити, рис. 1.19):
где J –момент инерции тела относительно оси, совпадающей с нитью, · Полнаяэнергия гармонического осциллятора:
· Закон сохранения энергии при гармонических колебаниях:
· Амплитуда Арезультирующего колебания
равна
· Начальная фаза результирующего колебания при сложении однонаправленных колебаний:
с амплитудами А1и А2 и начальными фазами
где · Возвращающая (квазиупругая) сила, действующая на тело массой m при гармонических колебаниях:
где х –смещение колеблющейся точки из положения равновесия; ω – циклическая частота колебаний; · Дифференциальное уравнение гармонических колебаний
где x – колеблющаяся величина; ω – круговая (циклическая) частота колебаний; · Дифференциальное уравнение затухающих колебаний
где r – коэффициент сопротивления (коэффициент пропорциональности между силой сопротивления и скоростью: · Кинематическое уравнение затухающих колебаний (рис.1.22):
Здесь
· Амплитуда затухающих колебаний:
где А0–амплитуда колебаний в момент t=0. · Логарифмический декремент затухания равен по определению логарифму отношения амплитуд
· Добротность
При условии
Если
· Дифференциальное уравнение вынужденных колебаний:
или в стандартной форме:
Здесь · Кинематическое уравнение вынужденных колебаний:
· Начальная фаза вынужденных колебаний:
· Резонансная частота:
· Максимальная амплитуда (амплитуда при резонансе):
Волны
где s – смещение частиц с координатой x из положения равновесия в момент времени t, A – амплитуда, ω – циклическая частота,
· Уравнениесферической волны:
Здесь s – смещение частиц с радиус-вектором
· Скорость распространения продольных и поперечных упругих волн в твёрдом теле:
где E – модуль Юнга, G – модуль сдвига, ρ – плотность. · Скорость звука в газе:
где Т – абсолютная температура, R – универсальная газовая постоянная, μ – молярная масса газа, γ – показатель Пуассона (для воздуха · Скорость распространения поперечной волны по струне:
где F – сила натяжения струны, S – площадь сечения струны, ρ – плотность. Задачи к разделу 1 1. Два тела бросили одновременно из одной точки: одно – вертикально вверх, другое – под углом 600 к горизонту. Начальная скорость каждого тела 25 м/с. Пренебрегая сопротивлением воздуха, найти расстояние между телами через 1,7 с. 2. Две частицы движутся с ускорением g в однородном поле силы тяжести. В начальный момент частицы находились в одной точке и имели скорости 3 м/с и 4 м/с, направленные горизонтально в противоположные стороны. Найти расстояние между частицами в момент, когда векторы их скоростей окажутся взаимно перпендикулярными. 3. Кабина лифта, у которой расстояние от пола до потолка равно 2,7 м, начала подниматься с постоянным ускорением 1,2 м/с2. Через 2 с после начала подъема с потолка кабины стал падать болт. Найти: а) время свободного падения болта; б) перемещение и путь болта за время свободного падения в системе отсчёта, связанной с шахтой лифта. 4. В момент времени t=0 частица вышла из начала координат в направлении, противоположном оси x. Её скорость меняется по закону 5. Материальная точка движется прямолинейно с ускорением а=5 м/с2. Определить, насколько путь, пройденный точкой в n-ю секунду, будет больше пути, пройденного в предыдущую секунду. Принять 6. Велосипедист ехал из одного пункта в другой. Первую треть пути он проехал со скоростью 7. Тело брошено с начальной скоростью с высоты h=2,4 м вверх под углом 8. Тело брошено с вышки в горизонтальном направлении со скоростью 20 м/с. Определить скорость тела и её направление в конце второй секунды после начала движения. 9. Твердое тело вращается вокруг неподвижной оси по закону 10. Точка движется по окружности радиусом R=30 см с постоянным угловым ускорением. Определить тангенциальное ускорение 11. На верхнем конце наклонной плоскости укреплен легкий блок, через который перекинута нить с грузами m1=5,1 кг и m2=2,2 кг на концах. Груз m1 скользит вниз по наклонной плоскости, поднимая висящий на другом конце нити груз m2. Угол наклонной плоскости с горизонтом 12. На верхнем конце наклонной плоскости укреплен легкий блок, через который перекинута нить с грузами m1=1,7 кг и m2=0,4 кг на концах. Груз m1 скользит вниз по наклонной плоскости, поднимая висящий на другом конце нити груз m2. Угол наклонной плоскости с горизонтом 13. На разных склонах наклонной плоскости, образующих с горизонтом углы 14. На разных склонах наклонной плоскости, образующих с горизонтом углы 15. Шарик массой m=45 г падает на горизонтальную поверхность стола с высоты h1=2,4 м и, отскочив, поднимается на некоторую высоту h2. Время соударения t=0,49 мс, средняя сила взаимодействия шарика со столом F=1200 Н. Найти h2. 16. Через блок перекинута нить, к концам которой подвешены гири массами m1=m2=1 кг. Какую силу нужно приложить к одной из гирь, чтобы гири стали двигаться с ускорением а=3 м/с2? Массой блока пренебречь. 17. Автомобиль массой m=5000 кг движется со скоростью 18. Какую наибольшую скорость может развивать велосипедист, проезжая закругление R=50 м, если коэффициент трения скольжения между шинами и асфальтом равен 0,3? Каков угол отклонения 19. Тело, двигаясь равноускоренно, соскользнуло с наклонной плоскости длиной l=2 м за время t=2 c. Определить коэффициент трения тела о плоскость. Угол наклона 20. Тело массой 0.2 кг движется прямолинейно, причем координата изменяется по закону x=A–Bt+5t2–t3 (время – в секундах, координата – в метрах). Найти силу, действующую на тело в конце второй секунды движения. 21. Две лодки массами m1=250 кг и m2=370 кг идут параллельными курсами со скоростями 22. Две лодки массами m1=310 кг и m2=160 кг идут параллельными курсами со скоростями 23. Снаряд, летящий со скоростью 24. Снаряд, летящий со скоростью 25. Человек массой m1=55 кг, стоящий на одном конце первоначально покоящейся тележки массой m2=120 кг и длиной l=4,5 м, прыгает со скоростью 26. Человек массой m1=45 кг, стоящий на одном конце первоначально покоящейся тележки массой m2=160 кг и длиной l=3,5 м, прыгает со скоростью 27. В деревянный шар массой m1=8 кг, подвешенный на нити длиной l=1,8 м, попадает горизонтально летящая пуля m2=4 г. С какой скоростью летела пуля, если нить с шаром и застрявшей в ней пулей отклонилась от вертикали на угол 28. Шар массой m1=5 кг движется со скоростью 29. Шар массой m1=2 кг сталкивается с покоящимся шаром большей массы и при этом теряет 40% кинетической энергии. Определить массу m2 большего шара. Удар считать абсолютно упругим, прямым, центральным. 30. Два груза массами m1=10 кг и m2=15 кг подвешены на нитях длиной l=2 м так, что грузы соприкасаются между собой. Меньший груз был отклонен на угол 31. Шайба массой m=50 г соскальзывает без начальной скорости по наклонной плоскости, составляющий угол 32. Из пружинного пистолета с жёсткостью пружины k=150 Н/м был произведен выстрел пулей массой m=8 г. Определить скорость пули при выстреле её из пистолета, если пружина была сжата на 4 см. 33. Молот массой m1=5 кг ударяет о небольшой кусок железа, лежащий на наковальне. Масса наковальни m2=100 кг. Массой куска железа пренебречь. Удар неупругий. Определить КПД удара молота при данных условиях. 34. Если на верхний конец вертикально расположенной спиральной пружины положить груз, то она сожмется на 3 мм. Насколько сожмет пружину тот же груз, упавший на конец пружины с высоты 8 см? 35. Определить работу растяжения двух последовательно соединённых пружин жесткостями k1=0,5 кН/м и k2=1 кН/м, если первая пружина при этом растянулась на 36. Две пружины жесткостями k1=400 Н/м и k2=250 Н/м соединены параллельно. Определить потенциальную энергию данной системы при абсолютной деформации 37. Из шахты глубиной h=600 м поднимают клеть массой m=3 т на канате, каждый метр которого имеет массу m1=1,5 кг. Какая работа совершается при поднятии клети на поверхность Земли? Каков КПД подъемного устройства? 38. Налетев на пружинный буфер, вагон массой m=16 т, двигавшийся со скоростью 39. Цепь длиной l=2 м лежит на столе, одним концом свисая со стола. Если длина свешивающейся части превышает 1/3 длины цепи, то цепь соскальзывает со стола. Определить скорость цепи в момент её отрыва от стола. 40. Материальная точка массой m=2 кг двигалась под действием некоторой силы согласно уравнению 41. Платформа, имеющая форму диска, может вращаться около вертикальной оси. На краю платформы стоит человек. На какой угол повернется платформа, если человек пойдет вдоль края платформы и, обойдя её, вернётся в исходную точку? Масса платформы m1=240 кг, масса человека m2=60 кг. Момент инерции человека рассчитывать как для материальной точки. 42. Маховик, вращающийся с постоянной угловой скоростью 43. Платформа в виде сплошного диска радиусом R=1,5 м и массой m1=180 кг вращается по инерции около вертикальной оси с частотой 44. По касательной к шкиву маховика в виде диска диаметром D=75 см и массой m=40 кг приложена сила F=10 Н. Определить угловое ускорение и частоту вращения маховика через 10 с после начала действия силы, если радиус шкива R= 12 см. Силой трения пренебречь. 45. Нить с привязанными к её концам грузами массой m1=50 г и m2=60 г перекинута через блок диаметром D=4 см. Определить момент инерции блока, если под действием силы тяжести грузов он получил угловое ускорение 46. Маховик в виде диска массой m=50 кг и радиусом R=20 см был раскручен до угловой скорости 47. На краю платформы в виде диска диаметром D=2 м, вращающейся по инерции вокруг вертикальной оси с частотой 48. Платформа в виде диска диаметром D=3 м и массой m1=180 кг может вращаться вокруг вертикальной оси. С какой угловой скоростью будет вращаться платформа, если по её краю пойдет человек массой m2=70 кг со скоростью 49. Блок, имеющий форму диска массой m=0,4 кг, вращается под действием силы натяжения нити, к концам которой подвешены грузы массами m1=0,3 кг и m2=0,7 кг. Определить силы натяжения нити по обе стороны блока. 50. Человек массой m2=60 кг стоит на краю неподвижной платформы в виде диска диаметром D=0.8 м и массой m1=20 кг. С какой угловой скоростью начнёт вращаться платформа, если человек поймает мяч массой m3=1 кг, летящий со скоростью 10 м/с по касательной к краю платформы? 51. Маховик в виде сплошного диска радиусом R=20 см и массой m=50 кг раскручен до частоты вращения 52. Маховик, массу которого m=5 кг можно считать распределенной по ободу радиусом R=20 см, свободно вращается вокруг горизонтальной оси, проходящей через его центр, с частотой 53. Вал в виде сплошного цилиндра массой m1=10 кг насажен на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря массой m2=2 кг. С каким ускорением будет опускаться гиря, если её предоставить самой себе? 54. Сплошной цилиндр массой m=4 кг катится без скольжения по горизонтальной поверхности. Линейная скорость оси цилиндра 55. Обруч и сплошной цилиндр, имеющие одинаковую массу m=2 кг, катятся без скольжения с одинаковой скоростью 56. Шар катится без скольжения по горизонтальной поверхности. Полная кинетическая энергия шара 14 Дж. Определить кинетическую энергию поступательного и вращательного движения шара. 57. Определить линейную скорость центра шара, скатившегося без скольжения с наклонной плоскости высотой h=1 м. 58. Сколько времени будет скатываться без скольжения обруч с наклонной плоскости длиной l=2 м и высотой h=0,1 м? 59. Якорь мотора вращается с частотой 60. Пуля массой m=10 г летит со скоростью 61. Уравнение колебаний точки имеет вид: 62. Точка совершает гармонические колебания по закону 63. Тело массой m=10 г совершает колебания по закону 64. Материальная точка массой m=50 г совершает гармонические колебания согласно уравнению 65. Математический маятник массой m=10 г и длиной l=1 м совершает гармонические колебания по закону 66. Физический маятник совершает малые колебания вокруг горизонтальной оси О с циклической частотой ω1=15 с-1. Если в положении равновесия к нему прикрепить под осью О на расстоянии l=20 см от неё небольшое тело массой m=0,05 кг, то частота колебаний становится ω2=10 с-1. Найти момент инерции первоначального маятника относительно оси О. 67. Логарифмический декремент затухания колебаний математического маятника длиной l=0,85 м равен 0.011. Определить, во сколько раз уменьшится полная механическая энергия маятника за время t=75 c. 68. Начальная амплитуда колебаний математического маятника А0=0,2 м. Амплитуда после 10 полных колебаний А10=0,01 м. Определить логарифмический декремент затухания и коэффициент затухания, если период колебаний Т=5 с. Записать уравнение колебаний. 69. Складываются два взаимно перпендикулярных колебания, выражаемых уравнениями 70. Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями 71. Плоская волна с периодом T=1.2 с и амплитудой А=2 см распространяется со скоростью υ=15 м/с. Чему равно смещение точки, находящейся на расстоянии l=45 м от источника волн, в тот момент, когда от начала колебаний источника прошло t=4 с? Колебания происходят по закону косинуса. 72. Плоская волна распространяется от источника колебаний вдоль прямой OX. Смещение точки из положения равновесия для момента времени t=T/2 составляет s=5 см. Точка удалена от источника колебаний на расстояние, равное l=l/3. Определить амплитуду колебаний. Колебания источника происходят по закону косинуса. 73. Плоская звуковая волна распространяется вдоль прямой со скоростью υ=300 м/с. Две точки, находящиеся на этой прямой на расстоянии l1=12 м и l2=15 м от источника, колеблются с разностью фаз Δφ=0.75p. Найти длину волны, написать уравнение волны и найти смещение обеих указанных точек в момент времени, равный t=1.2 с, если амплитуда колебаний А=1 мм. Колебания происходят по закону косинуса. 74. Скорость звука в воде υ=1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна ν=725 Гц? 75. Смещение от положения равновесия точки, находящейся на расстоянии l=4 см от источника колебаний, колеблющегося по закону: s=sin(ωt),в момент времени t=T/6 равно половине амплитуды (s выражено в метрах, t – в секундах). Найти длину волны. Волна плоская. 76. Уравнение незатухающих колебаний дано в виде 77. Два источника колебаний, лежащие в точках с координатами х1=0 м х2=10 м, колеблются по одинаковому закону 78. Определить разность фаз Δφ колебаний двух точек среды, находящихся на расстоянии Δl=0.1 м друг от друга, если в среде распространяется плоская волна вдоль линии, соединяющей эти точки. Скорость распространения волны υ=314 м/с, частота колебаний источника ν=1000 Гц. 79. Два точечных когерентных источника звуковых волн одинаковой мощности находятся в воздухе на расстояниях l1=2.5 м и l2=2.4 м от микрофона. Определить отношение амплитуд результирующего и исходного колебаний, если длина волны λ=0.3 м. 80. Для звуковой волны, описываемой уравнением
Раздел 2. ГИДРОДИНАМИКА. |
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 601. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

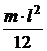





 ,
, – момент инерции этого тела относительно оси, проходящей через центр масс тела параллельно заданной оси;
– момент инерции этого тела относительно оси, проходящей через центр масс тела параллельно заданной оси;  – расстояние между осями; m – масса тела (рис. 1.15).
– расстояние между осями; m – масса тела (рис. 1.15).
 ,
, – его угловая скорость.
– его угловая скорость.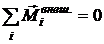 , то
, то  ,
, ,
,
 ,
,  ,
, 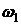 и
и 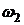 – моменты инерции и угловые скорости тел до взаимодействия:
– моменты инерции и угловые скорости тел до взаимодействия:  ,
,  ,
,  и
и  – те же величины после взаимодействия.
– те же величины после взаимодействия. ,
, тела прямо пропорционально суммарному моменту
тела прямо пропорционально суммарному моменту  внешних сил и обратно пропорционально моменту инерции
внешних сил и обратно пропорционально моменту инерции  .
. равно импульсу
равно импульсу  суммарного момента
суммарного момента  внешних сил:
внешних сил: , или
, или  .
.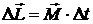 , или
, или  ,
, (или
(или  ) – промежуток времени, в течение которого действовал момент сил
) – промежуток времени, в течение которого действовал момент сил  при вращательном движении:
при вращательном движении: ,
,  .
. ), то работа равна
), то работа равна .
. (или
(или  ) – угол поворота.
) – угол поворота. .
. .
. ,
, – кинетическая энергия поступательного движения тела;
– кинетическая энергия поступательного движения тела;  – скорость центра масс тела;
– скорость центра масс тела;  – кинетическая энергия вращательного движения тела вокруг оси, проходящей через центр масс.
– кинетическая энергия вращательного движения тела вокруг оси, проходящей через центр масс. ,
, – начальная фаза колебаний;
– начальная фаза колебаний; – фаза колебаний в момент t.
– фаза колебаний в момент t. , или
, или  ,
, и Т – частота (линейная частота) и период колебаний соответственно.
и Т – частота (линейная частота) и период колебаний соответственно. .
. .
. .
.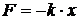 , и в пренебрежении массой пружины в сравнении с массой тела.
, и в пренебрежении массой пружины в сравнении с массой тела. ,
,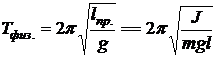 .
. – приведённая длина физического маятника (то есть длина такого математического маятника, который имеет тот же период колебаний).
– приведённая длина физического маятника (то есть длина такого математического маятника, который имеет тот же период колебаний).
 ,
,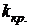 – модуль кручения нити. Формула справедлива для упругих колебаний в пределах, в которых выполняется закон Гука:
– модуль кручения нити. Формула справедлива для упругих колебаний в пределах, в которых выполняется закон Гука:  . Здесь M – момент упругой силы, возникающей при закручивании нити на угол
. Здесь M – момент упругой силы, возникающей при закручивании нити на угол  .
.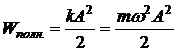
 .
. , полученного при сложении двух колебаний одинаковой частоты, происходящих по одной прямой,
, полученного при сложении двух колебаний одинаковой частоты, происходящих по одной прямой, и
и ,
, ,
, где А1и А2 – амплитуды исходных колебаний;
где А1и А2 – амплитуды исходных колебаний;  и
и  – их начальные фазы (см. сложение колебаний по методу векторных диаграмм на рис. 1.20).
– их начальные фазы (см. сложение колебаний по методу векторных диаграмм на рис. 1.20). .
. · Уравнение траектории (рис. 1.21) точки, участвующей в двух взаимно перпендикулярных колебаниях одинаковой частоты,
· Уравнение траектории (рис. 1.21) точки, участвующей в двух взаимно перпендикулярных колебаниях одинаковой частоты, и
и 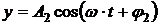 ,
, ,
, – сдвиг фаз колебаний.
– сдвиг фаз колебаний.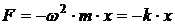 ,
,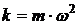 – коэффициент пропорциональности. В частном случае пружинного маятника он равен жёсткости пружины.
– коэффициент пропорциональности. В частном случае пружинного маятника он равен жёсткости пружины.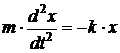 , или в стандартной форме:
, или в стандартной форме: ,
,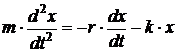 , или в стандартной форме:
, или в стандартной форме: ,
,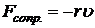 );
);  – коэффициент затухания;
– коэффициент затухания;  – круговая частота собственных (незатухающих) колебаний.
– круговая частота собственных (незатухающих) колебаний.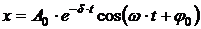 , или
, или  .
. – круговая частота затухающих колебаний:
– круговая частота затухающих колебаний: .
.
 ,
, и
и  двух следующих друг за другом колебаний, то есть колебаний, отстоящих во времени друг от друга на один период (рис. 1.22):
двух следующих друг за другом колебаний, то есть колебаний, отстоящих во времени друг от друга на один период (рис. 1.22): , или
, или  , или
, или  .
.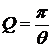 .
. (затухание мало):
(затухание мало): .
. за один период:
за один период: .
. ,
, .
. – вынуждающая сила (внешняя периодическая сила, действующая на колеблющуюся материальную точку и вызывающая вынужденные колебания);
– вынуждающая сила (внешняя периодическая сила, действующая на колеблющуюся материальную точку и вызывающая вынужденные колебания);  – её амплитудное значение; ω – её циклическая частота;
– её амплитудное значение; ω – её циклическая частота;  ;
;  .
. · Амплитуда вынужденных колебаний как функция частоты (рис. 1.23):
· Амплитуда вынужденных колебаний как функция частоты (рис. 1.23):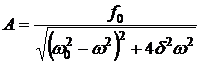 .
. .
. .
.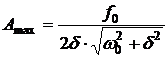 .
. · Уравнение плоской волны, бегущей в положительном направлении оси OX (рис. 1.24):
· Уравнение плоской волны, бегущей в положительном направлении оси OX (рис. 1.24): ,
, – волновое число (модуль волнового вектора),
– волновое число (модуль волнового вектора), – фазовая скорость (скорость распространения фиксированной фазы волны
– фазовая скорость (скорость распространения фиксированной фазы волны  ),
), – длина волны (расстояние, на которое распространяется волна за время, равное периоду колебаний),
– длина волны (расстояние, на которое распространяется волна за время, равное периоду колебаний), ,
, из положения равновесия в момент времени t;
из положения равновесия в момент времени t; – волновой вектор, равный по величине
– волновой вектор, равный по величине  – амплитуда сферической волны; r – расстояние до источника.
– амплитуда сферической волны; r – расстояние до источника. ,
,  ,
, ,
, ).
). ,
, , где
, где  см/с – модуль начальной скорости; Т=5 с. Найти: а) координату х частицы в моменты времени 6 с, 10 с и 20 с; б) моменты времени, когда частица будет находиться на расстоянии 10 см от начала координат; в) путь S, пройденный частицей за первые 4 с и 8 с; г) изобразить примерный график S(t).
см/с – модуль начальной скорости; Т=5 с. Найти: а) координату х частицы в моменты времени 6 с, 10 с и 20 с; б) моменты времени, когда частица будет находиться на расстоянии 10 см от начала координат; в) путь S, пройденный частицей за первые 4 с и 8 с; г) изобразить примерный график S(t). .
. км/ч. Далее половину оставшегося времени он ехал со скоростью
км/ч. Далее половину оставшегося времени он ехал со скоростью  км/ч, после чего до конечного пункта он шел пешком со скоростью
км/ч, после чего до конечного пункта он шел пешком со скоростью  км/ч. Определить среднюю скорость велосипедиста.
км/ч. Определить среднюю скорость велосипедиста. =350 к горизонту и упало на расстоянии l=37 м от места бросания. Найти начальную скорость тела.
=350 к горизонту и упало на расстоянии l=37 м от места бросания. Найти начальную скорость тела. , где а=6 рад/с, b=2 рад/с3. Найти: а) средние значения угловой скорости и углового ускорения за промежуток времени от начала вращения до остановки; б) угловое ускорение в момент остановки тела.
, где а=6 рад/с, b=2 рад/с3. Найти: а) средние значения угловой скорости и углового ускорения за промежуток времени от начала вращения до остановки; б) угловое ускорение в момент остановки тела. точки, если известно, что за время 4 с она совершила три оборота и в конце третьего оборота её нормальное ускорение
точки, если известно, что за время 4 с она совершила три оборота и в конце третьего оборота её нормальное ускорение  =2,7 м/с2.
=2,7 м/с2. 320 и
320 и  480, находятся грузы m1=3,3 кг и m2. Нить, связывающая грузы, перекинута через легкий блок, укрепленный на вершине наклонной плоскости. Коэффициент трения между грузами и наклонной плоскостью равен 0,1, ускорение грузов а= –1,2 м/с2 (а > 0, если система движется в сторону груза m2). Определить массу второго груза m2.
480, находятся грузы m1=3,3 кг и m2. Нить, связывающая грузы, перекинута через легкий блок, укрепленный на вершине наклонной плоскости. Коэффициент трения между грузами и наклонной плоскостью равен 0,1, ускорение грузов а= –1,2 м/с2 (а > 0, если система движется в сторону груза m2). Определить массу второго груза m2. 10 м/с по выпуклому мосту. Определить силу давления автомобиля на мост в его верхней точке, если радиус кривизны моста R=50 м.
10 м/с по выпуклому мосту. Определить силу давления автомобиля на мост в его верхней точке, если радиус кривизны моста R=50 м.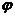 велосипеда от вертикали, когда велосипедист движется по закруглению?
велосипеда от вертикали, когда велосипедист движется по закруглению? 300.
300. =1,6 м/с и
=1,6 м/с и  . Когда лодки оказываются рядом, из каждой лодки в другую перекладывается мешок массой m=32 кг, после чего лодки продолжают двигаться параллельными курсами, но со скоростями u1 и u2=2,1 м/с. Найти скорость u1.
. Когда лодки оказываются рядом, из каждой лодки в другую перекладывается мешок массой m=32 кг, после чего лодки продолжают двигаться параллельными курсами, но со скоростями u1 и u2=2,1 м/с. Найти скорость u1. относительно земли под углом
относительно земли под углом 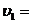 1 м/с и сталкивается с покоящимся шаром массой m2=2 кг. Определить скорости шаров после удара. Удар считать абсолютно упругим, прямым, центральным.
1 м/с и сталкивается с покоящимся шаром массой m2=2 кг. Определить скорости шаров после удара. Удар считать абсолютно упругим, прямым, центральным. 2 см.
2 см. 8 см. Найти общую жесткость пружин буфера.
8 см. Найти общую жесткость пружин буфера. , где А=10 м, В= –2 м/с, С=1 м/с2, D= –0,2 м/с3. Найти мощность, развиваемую при движении, в моменты времени
, где А=10 м, В= –2 м/с, С=1 м/с2, D= –0,2 м/с3. Найти мощность, развиваемую при движении, в моменты времени 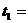 2 c и
2 c и 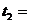 5 c.
5 c. 62,8 рад/с, при торможении начал вращаться равнозамедленно. Когда торможение прекратилось, вращение маховика снова сделалось равномерным, но уже с угловой скоростью
62,8 рад/с, при торможении начал вращаться равнозамедленно. Когда торможение прекратилось, вращение маховика снова сделалось равномерным, но уже с угловой скоростью  37,7 рад/с. Определить угловое ускорение маховика и продолжительность торможения, если за время равнозамедленного движения маховик сделал N=50 оборотов.
37,7 рад/с. Определить угловое ускорение маховика и продолжительность торможения, если за время равнозамедленного движения маховик сделал N=50 оборотов. 10 об/мин. В центре платформы стоит человек массой m2=60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы?
10 об/мин. В центре платформы стоит человек массой m2=60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы?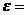 1,5 рад/с2.
1,5 рад/с2. 50 рад/с и затем предоставлен самому себе. Под влиянием трения маховик остановился. Найти момент сил трения, считая его постоянным, принимая во внимание, что: а) маховик остановился через 50 с; б) маховик остановился, сделав 200 оборотов.
50 рад/с и затем предоставлен самому себе. Под влиянием трения маховик остановился. Найти момент сил трения, считая его постоянным, принимая во внимание, что: а) маховик остановился через 50 с; б) маховик остановился, сделав 200 оборотов. 0,13 Гц, стоит человек массой m=70 кг. Когда человек перешёл в центр платформы, она стала вращаться с частотой
0,13 Гц, стоит человек массой m=70 кг. Когда человек перешёл в центр платформы, она стала вращаться с частотой  0,16 Гц. Определить массу платформы.
0,16 Гц. Определить массу платформы.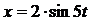 (смещение из положения равновесия выражено в метрах, время – в секундах). Определить максимальные значения скорости и ускорения точки.
(смещение из положения равновесия выражено в метрах, время – в секундах). Определить максимальные значения скорости и ускорения точки. . В какой момент времени её потенциальная энергия равна кинетической энергии?
. В какой момент времени её потенциальная энергия равна кинетической энергии? , где x0=2 см; ω=4π рад/с. Найти функциональную зависимость от времени силы, действующей на тело, и его кинетической энергии; вычислить их максимальные значения.
, где x0=2 см; ω=4π рад/с. Найти функциональную зависимость от времени силы, действующей на тело, и его кинетической энергии; вычислить их максимальные значения. (здесь x0=0.05 м). Определить: а) возвращающую силу F для момента времени t=0,5 с; б) полную энергию материальной точки.
(здесь x0=0.05 м). Определить: а) возвращающую силу F для момента времени t=0,5 с; б) полную энергию материальной точки. (рад). Определить силу натяжения в момент времени t=T/2.
(рад). Определить силу натяжения в момент времени t=T/2. см и
см и  см. Найти уравнение траектории и построить её на чертеже, показав направление движения точки.
см. Найти уравнение траектории и построить её на чертеже, показав направление движения точки. см и
см и 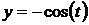 см. Найти уравнение траектории и построить её на чертеже.
см. Найти уравнение траектории и построить её на чертеже. (смещение из положения равновесия – в см, время – в с). Найти смещение от положения равновесия, скорость и ускорение точки, находящейся на расстоянии l=20 м от источника колебаний, для момента времени t=1 с после начала колебаний. Скорость распространения волны υ=100 м/с. Волна плоская.
(смещение из положения равновесия – в см, время – в с). Найти смещение от положения равновесия, скорость и ускорение точки, находящейся на расстоянии l=20 м от источника колебаний, для момента времени t=1 с после начала колебаний. Скорость распространения волны υ=100 м/с. Волна плоская. (смещение из положения равновесия – в метрах, время – в секундах). Написать уравнение колебаний в точке А, координата которой равна хА=13 м. Скорость распространения волн равна 320 м/с. Волны считать плоскими.
(смещение из положения равновесия – в метрах, время – в секундах). Написать уравнение колебаний в точке А, координата которой равна хА=13 м. Скорость распространения волн равна 320 м/с. Волны считать плоскими. , где амплитуда выражена в метрах, круговая частота – в с-1, волновое число – в м-1, найти: а) скорость распространения волны υ; б) амплитуду скорости частиц среды υmax и её отношение к скорости распространения волны
, где амплитуда выражена в метрах, круговая частота – в с-1, волновое число – в м-1, найти: а) скорость распространения волны υ; б) амплитуду скорости частиц среды υmax и её отношение к скорости распространения волны  ; в) длину волны λ и отношение амплитуды смещения частиц среды к длине волны
; в) длину волны λ и отношение амплитуды смещения частиц среды к длине волны  .
.