
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Динамика материальной точки· Второй закон Ньютона (уравнение движения материальной точки):
где · Второй закон Ньютона в импульсной форме:
где Если сила
где · Второй закон Ньютона в проекциях:
или
· Третий закон Ньютона (рис. 1.7):
· Закон всемирного тяготения (сила гравитационного притяжения):
где · Сила тяжести
где · Вес тела – сила, приложенная к подставке или подвесу (рис. 1.8). Вес тела, движущегося с ускорением
где m – масса тела. Если ускорение тела направлено вертикально вверх, то вес · Сила трения скольжения(рис. 1.9):
где · Сила трения покоя:
· Сила упругости (закон Гука):
где k – коэффициент упругости (жесткость пружины),
где  · Плотность тела:
· Уравнение движения центра масс:
где · Закон сохранения импульса: если сумма внешних сил равна нулю, то полный импульс системы сохраняется. Если или где N – число материальных точек (или тел), входящих в систему. · Работа, совершаемая постоянной силой
· Работа, совершаемая переменной силой
где интегрирование производится вдоль траектории (рис. 1.12).
· Мгновенная мощность:
где · Коэффициент полезного действия
· Закон изменения полной энергии для незамкнутой системы: · Закон изменения механической энергии для незамкнутой системы: Wмех.1=Wмех.2+Асистемы против внешних сил+Асистемы против диссипативных сил · Кинетическая энергия материальной точки (или тела), движущейся поступательно:
· Потенциальная
В проекциях: Здесь
· Закон сохранения полной энергии: Если Здесь · Закон сохранения механической энергии (выполняется в замкнутой системе, в которой действуют только консервативные силы): Если Здесь · Потенциальная энергия упруго деформированного тела (сжатой или растянутой пружины)
где k – жёсткость пружины, · Потенциальная энергия гравитационного взаимодействия
где r – расстояние между двумя точечными массами m1, и m2, · Потенциальная энергия тела в однородном поле силы тяжести:
где h – высота тела над уровнем, принятым за нулевой, g – ускорение свободного падения. Эта формула справедлива при условии |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 490. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , или
, или  ,
, – равнодействующая всех N сил, приложенных к телу (векторная сумма всех сил), m – его масса,
– равнодействующая всех N сил, приложенных к телу (векторная сумма всех сил), m – его масса,  – его ускорение.
– его ускорение.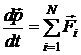 ,
, – импульс тела (материальной точки),
– импульс тела (материальной точки),  – его скорость.
– его скорость. , действующая на тело, постоянна, то
, действующая на тело, постоянна, то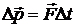 ,
, – промежуток времени, в течение которого действовала сила
– промежуток времени, в течение которого действовала сила  – изменение импульса тела.
– изменение импульса тела.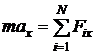 ;
;  ;
;  ,
, ;
;  ;
;  ,
, где под знаком суммы стоят проекции силна соответствующие оси координат.
где под знаком суммы стоят проекции силна соответствующие оси координат. .
. ,
, – гравитационная постоянная; m1 и m2 – массы взаимодействующих тел, рассматриваемые как материальные точки; r – расстояние между ними.
– гравитационная постоянная; m1 и m2 – массы взаимодействующих тел, рассматриваемые как материальные точки; r – расстояние между ними.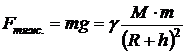 ,
, – ускорение свободного падения, M – масса Земли, R – радиус Земли, h – высота тела массой m над Землёй.
– ускорение свободного падения, M – масса Земли, R – радиус Земли, h – высота тела массой m над Землёй. , равен
, равен ,
, ; а если вертикально вниз, то
; а если вертикально вниз, то  .
. ,
,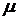 – коэффициент трения, N – сила нормального давления.
– коэффициент трения, N – сила нормального давления. .
. ,
, – абсолютная деформация (рис. 1.10).
– абсолютная деформация (рис. 1.10).
 и координаты центра масс системы материальных точек:
и координаты центра масс системы материальных точек: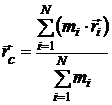 ;
; ,
,  ,
,  ,
, – масса i-той материальной точки;
– масса i-той материальной точки; 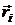 ,
,  ,
,  ,
, 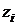 – её радиус-вектор и координаты;
– её радиус-вектор и координаты;  – масса всей системы; N число точек.
– масса всей системы; N число точек. .
. ,
,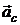 – ускорение центра масс;
– ускорение центра масс;  – сумма всех внешних сил, приложенных к системе.
– сумма всех внешних сил, приложенных к системе. , то
, то  ,
, , или
, или  .
. , или
, или  ,
, где
где  – перемещение,
– перемещение,  – угол между направлениями векторов силы
– угол между направлениями векторов силы  (рис. 1.11):
(рис. 1.11): ,
, · Средняя мощность за интервал времени
· Средняя мощность за интервал времени  .
. , или
, или  ,
, – работа, совершаемая за промежуток времени
– работа, совершаемая за промежуток времени  ,
,  .
. , или Wполн.1=Wполн.2+Асистемы против внешних сил
, или Wполн.1=Wполн.2+Асистемы против внешних сил  , или
, или  .
. энергия тела и консервативная сила, действующая на тело в данной точке поля, связаны соотношением:
энергия тела и консервативная сила, действующая на тело в данной точке поля, связаны соотношением: , или
, или  .
. ,
,  ,
,  .
. ,
,  и
и  – единичные векторы (орты). В частном случае, когда поле сил обладает сферической симметрией (как, например, гравитационное),
– единичные векторы (орты). В частном случае, когда поле сил обладает сферической симметрией (как, например, гравитационное), .
. , то
, то  .
. и
и  – полная энергия системы; сумма всех видов энергии для начального и конечного состояния системы соответственно.
– полная энергия системы; сумма всех видов энергии для начального и конечного состояния системы соответственно. и
и  – полная механическая энергия системы; сумма всех видов потенциальной и кинетической энергии для начального и конечного состояния системы соответственно (
– полная механическая энергия системы; сумма всех видов потенциальной и кинетической энергии для начального и конечного состояния системы соответственно (  ).
).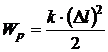 ,
, – абсолютная деформация.
– абсолютная деформация. ,
, ,
, , где R – радиус Земли.
, где R – радиус Земли.