Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Формула повної ймовірності та формула Байеса.Нехай подія А може відбутися тільки за умови настання однієї із несумісних подій
де Наведена залежність називається формулою повної ймовірності. Подія А може відбутись одночасно з деякою із подій
Означення повторних незалежних випробувань. Нехай проводяться n випробувань, у кожному з яких подія А може як відбутись, так і не відбутись. Якщо ця ймовірність у кожному випробуванні не залежить від того, відбулась вона в інших випробуваннях чи ні, то такі випробування називаються незалежними щодо події А. Згідно з означенням випробування також незалежні, якщо в кожному з них імовірність настання події А однакова, тобто дорівнює тому самому числу. Імовірність того, що подія А відбудеться в кожному з незалежних випробувань, позначають
Формула Бернуллі для обчислення ймовірності і наймовірнішого числа. Імовірність того, що в n незалежних випробуваннях, у кожному з яких імовірність Р(А) = р, подія А відбудеться m раз, подається так:
Імовірність того, що в результаті n незалежних експериментів подія А з’явиться від mi до mj раз, обчислюється так: Локальна та інтегральна теореми Мавра-Лапласа. Локальна теорема Лапласа. Імовірність того, що в n незалежних випробуваннях, у кожному з яких Р(А) = р, подія А відбудеться m раз, подається такою наближеною залежністю: 
Локальна теорема Лапласа дає змогу обчислювати ймовірності Інтегральна теорема Лапласа. Імовірність того, що подія А відбудеться від
Значення функції Лапласа наводяться у спеціальних таблицях. Формула Пуассона малоймовірних випадкових подій.
Точність асимптотичних формул для великих значень n- числа повторних незалежних експериментів за схемою Бернуллі – знижується з наближенням p- до нуля .Тому при n → R, p- 0 за умови np=a=const імовірність появи випадкової події m раз (0<=m <=n),обчислюється за такою асимптотичною формулою: Якщо в кожному з n незалежних повторних випробувань
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 648. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
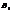 (i = 1, 2,…, n), які утворюють повну групу. Тоді ймовірність події А подається формулою:
(i = 1, 2,…, n), які утворюють повну групу. Тоді ймовірність події А подається формулою: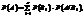
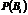 — імовірність події
— імовірність події 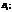
 — умовні ймовірності настання події А.
— умовні ймовірності настання події А. Відомі ймовірності подій
Відомі ймовірності подій 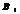 та умовні ймовірності того, що подія А відбудеться. Відомо, що в результаті випробування подія А відбулась. Потрібно з огляду на це переоцінити ймовірності гіпотез
та умовні ймовірності того, що подія А відбудеться. Відомо, що в результаті випробування подія А відбулась. Потрібно з огляду на це переоцінити ймовірності гіпотез 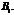 Для цього застосовують формулу Баєса:
Для цього застосовують формулу Баєса: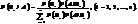
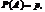 а ймовірність настання протилежної події
а ймовірність настання протилежної події 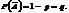
 Формула застосовується, якщо
Формула застосовується, якщо 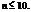
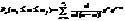
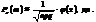

 , якщо n > 10 i p > 0,1.
, якщо n > 10 i p > 0,1.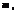 до
до  раз при проведенні n незалежних випробувань, у кожному з яких подія А відбувається з імовірністю р, подається формулою:
раз при проведенні n незалежних випробувань, у кожному з яких подія А відбувається з імовірністю р, подається формулою: —функція Лапласа;
—функція Лапласа;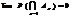
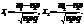

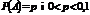 , а n велике, то
, а n велике, то