Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема Мэя: нормативная оценка правила большинства.Наиболее важная теорема о правиле большинства была доказана полвека назад Мэем (May, 1952). Строгое предпочтение альтернативы х альтернативе у имеет место в тех и только тех случаях, когда субъект выбора оценивает первую возможность выше второй. Соответствующее строгое предпочтение i-го индивида записывается хР1у, а аналогичный результат коллективного выбора — хРу. Нестрогое предпочтениеальтернативы х альтернативе у означает, что, с точки зрения делающего выбор субъекта, первая альтернатива лучше или равноценна второй. Нестрогие индивидуальное и коллективное предпочтения обозначаются xR1у и xRy. Равноценностьдвух альтернатив для i-го индивида записывается хI1у, а соответствующий результат коллективного выбора — xIy. Пусть F1 — индивидуальная функция решения, которая определяется сле- дующим образом: Fi(x,y) =1, когда хРi у, Fi (х,у) = 0, когда уIiх, Fi (x,y) = -1, когда хРiу. F= F(F1 , F2,..., Fn) — групповая функция решения, значения которой зависят от результатов коллективного выбора в группе, состоящей из п членов. Если применяется правило простого большинства, то: F = 1, когда Σ Fi > 0, F = 0, когда Σ Fi = 0, F = -1, когда Σ Fi < 0. Американский исследователь Кеннет Мэй доказал, что применение правила простого большинства — единственная процедура коллективного выбора, удовлетворяющая сле- дующим четырем условиям: однозначность, анонимность, нейтральность, положительное реагирование. 1. Однозначность: для заданного набора предпочтений, функция решения группы означает выбор x или y как наилучшего элемента либо указывает на равнозначность обоих вариантов. Групповая функция решения принимает одно и только одно значение для каждой пары альтернатив.  2. Анонимность: "сдвиг" предпочтений одного из членов сообщества, скажем, от xPi, y к yPi, x и обратный сдвиг любого другого члена (от yPj, x к xPj, y) оставляет конечный результат для сообщества неизменным. Значение F зависит от числа положительных, нулевых и отрицательных значений индивидуальных функций решения, но не зависит от того, кто именно из членов группы принял то или иное индивидуальное решение. 3. Нейтральность: Если для какого-то набора индивидуальных предпочтений верно хРу, и всем участникам выбора присущи те же порядковые (ординальные) предпочтения по отношению к паре z и w, что и по отношению к паре х и у (т. е. для всякого i имеет место zRiw, когда xRiy), то zPw. 4. Свойство положительного реагирования: если результатом конечного решения является xRy, и предпочтения одного из избирателей изменяются от yRi,x к xRi,y или от xi,y к xPi,y при неизменности предпочтений всех прочих избирателей, то в результате коллективного решения должно содержать xPy. На основании теоремы Мэя мы можем прийти к выводу о том, что при установлении данных четырех условий число возможных правил голосования сокращается до одного, а именно, правила простого большинства. Идентичность правила большинства этим четырем условиям предполагает, что все нормативные черты, которые присущи правилу большинства, (справедливости равенства) - заключены в этих четырех аксиомах, поскольку последние представляют его оборотную сторону. Нормативное ядро теоремы заключено прежде всего в аксиомах анонимности и нейтральности. Нейтральность представляет собой независимость предпочтений от других предпочтений. Когда речь идет о некоторой паре вариантов, рассматриваются только те предпочтения, которые относятся к этой паре. Информация, касающаяся других предпочтений избирателей, исключается, что устраняет одну из возможностей сравнить интенсивности предпочтений. Нейтральность предполагает, что подход к каждому выбору одинаков, независимо от того, о чем конкретно идет речь. Таким образом, вопрос о том, какого цвета должны быть лампочки на рождественской елке, красного или голубого, решается таким же образом, как и вопрос о том, следует ли конфисковать имущество Джона Доу и распределить его между остальными членами общества, а именно, на основе взвешивания индивидуальных шкал предпочтений. В то время как аксиома нейтральности означает, что все выборы рассматриваются одинаковым образом, анонимность предполагает одинаковый подход к самим избирателям. Можно представить множество проблем, в отношении которых это целесообразно. Когда речь идет о том, какого цвета должны быть рождественские лампочки, изменение предпочтений одного из избирателей от красного к голубому при одновременном изменении предпочтений другого от голубого к красному, вероятно, не должно повлиять на конечный результат. Неявно здесь предполагается, что цвет елочных огней имеет примерно одно и то же значение для всех избирателей. Данная предпосылка о равных интенсивностях предпочтений встроена в процедуру голосования. Требование анонимности исключает влияние на выбор индивидуальных признаков голосующего, а требование нейтральности — уникальных признаков конкретной альтернативы (в ходе доказательства единственными признаками альтернатив выступают их имена, которые, однако, можно изменять, не вступая в противоречие с условиями). Тем самым формально закрепляется значимость одного только числа голосов, поданных за ту или иную альтернативу. В то же время требование достижимости результата исключает различные варианты правила квалифицированного большинства. Две аксиомы: анонимность и нейтральность, предполагают абстрагирование от интенсивности предпочтений. В самом деле, анонимность, по сути, означает, что, даже если предпочтения двух индивидов существенно различаются по интенсивности (скажем, один готов заплатить за победу наиболее желательной для него альтернативы намного больше, чем другой), они в одинаковой мере влияют на коллективное решение. Фактически в этом заключается принцип "один человек — один голос". Нейтральность предполагает, что две пары альтернатив трактуются единообразно, если касающиеся их предпочтения всего лишь однонаправлены, тогда как интенсивность этих предпочтений не принимается во внимание.
33. Цикличность (парадокс Кондорсе). Теорема о медианном избирателе. Парадокс Кондорсе́ заключается в том, что при наличии более двух альтернатив и более двух избирателей коллективная ранжировка альтернатив может быть цикличной, даже если ранжировки всех избирателей не являются цикличными Согласно принципу Кондорсе, для определения истинной воли большинства необходимо, чтобы каждый голосующий проранжировал всех кандидатов в порядке их предпочтения. Таким образом, по Кондорсе воля большинства выражается в виде трех суждений C > B > A и если необходимо выбрать одного из кандидатов, то, согласно принципу Кондорсе, следует предпочесть кандидата С. Парадокс Кондорсе 1 человек:
1 человек: 1 человек: по итогам голосования выделяются три утверждения:
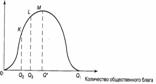
Теорема о «медианном избирателе». При симметричном распределении предпочтений относительно конкретного общественного блага, максимизация голосов избирателей достигается при ориентации на количество общественного блага Q*, предпочтительное с точки зрения «медианного избирателя». Название теоремы связано с тем, что позиция Q* соответствует медиане политического спектра; иными словами, варианты Q < Q* и Q > Q* поддерживаются одинаковым количеством избирателей.
Если Q1 = 100 и Q* = 50, то партии 1 целесообразно заявить предвыборную платформу, ориентированную на предоставление 50 единиц общественного блага, а партии 2 целесообразно анонсировать предоставление 51 единицы общественного блага. Тогда партия 1 получит число голосов, соответствующее площади фигуры ОМQ*, а число голосов, полученных партией 2, будет представлено площадью фигуры Q*МQ1. Отклонение от ориентации на медианного избирателя ведет к потере голосов. Если партия 1 анонсирует предоставление количества общественного блага Q2, то ее позиция окажется привлекательной лишь для тех избирателей, которые предпочитают производство не более количества Q3 общественного блага. Таким образом, партия 2 получит число голосов, соответствующее площади фигуры Q3LМQ1, в то время как число голосов, полученное партией 1, окажется гораздо меньше (оно будет соответствовать площади фигуры QКLQ3).Можно видеть, что справедливость теоремы о «медианном избирателе» зависит от специфической формы распределения предпочтений избирателей.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 1021. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
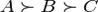
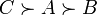
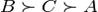
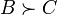 ,
,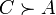 ,
,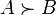 . Но вместе эти утверждения противоречивы. В этом и состоит парадокс (эффект) Кондорсе (или парадокс голосования). В этом случае оказывается невозможным принять какое-то согласованное решение и определить волю большинства. ПРИМЕРПусть у нас имеются три голосующих человека. Первый из них голосует «да» по первому вопросу, «да» по второму и «нет» по третьему («да»/«да»/«нет»), второй — «да»/«нет»/«да», третий — «нет»/«да»/«да». Суммарный итог голосования подсчитывается как соотношение сумм голосов «да» и «нет» по каждому из вопросов. В рассмотренном случае суммарный итог голосования будет «да»/«да»/«да». Этот итог не отражает мнения ни одного из голосовавших и, естественно, не удовлетворяет никого.
. Но вместе эти утверждения противоречивы. В этом и состоит парадокс (эффект) Кондорсе (или парадокс голосования). В этом случае оказывается невозможным принять какое-то согласованное решение и определить волю большинства. ПРИМЕРПусть у нас имеются три голосующих человека. Первый из них голосует «да» по первому вопросу, «да» по второму и «нет» по третьему («да»/«да»/«нет»), второй — «да»/«нет»/«да», третий — «нет»/«да»/«да». Суммарный итог голосования подсчитывается как соотношение сумм голосов «да» и «нет» по каждому из вопросов. В рассмотренном случае суммарный итог голосования будет «да»/«да»/«да». Этот итог не отражает мнения ни одного из голосовавших и, естественно, не удовлетворяет никого.