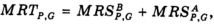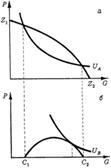
Эффективный объем общественных благ в модели общего равновесия.

Если, выбирая объем их предоставления, мы будем основываться только на решениях отдельных индивидов, принятых исходя из гипотезы о максимизации полезности, очевидно, что, с точки зрения всей совокупности индивидов, общественных благ будет предоставлено недостаточно. Индивид при покупке блага не принимает во внимание выгод (внешних эффектов), которые могут получить другие потребители, пользующиеся благом бесплатно. По этой причине общественное благо будет предоставлено в меньшем объеме, чем следовало бы, с учетом всех возможных выгод.

Модель оптимального размещения ресурсов в экономике при наличии двух типов благ (частного и общественного) была предложена П. Самуэльсоном в середине 1950-х гг.

Рассмотрим сначала графическое решение проблемы оптимального размещения ресурсов при наличии общественного блага.

Предположим, что в экономике производятся только два потребительских блага - частное (P) и общественное (G). Имеются два потребителя (A и B) со своими функциями полезности, которым соответствуют кривые безразличия UA и UB. Функция трансформации представлена на графике кривой производственных возможностей Z1Z2

Для вывода условия парето-оптимальности зафиксируем полезность, получаемую индивидом A на уровне UA. Тогда при заданной кривой производственных возможностей Z1Z2 можно найти количество частного блага P, доступного второму индивиду, B (по определению весь объем общественного блага доступен обоим индивидам, соперничества за его потребление не возникает). На рис. 4,б граница набора потребительских возможностей индивида B обозначена C1C2. Она получена как вертикальная разность между кривой производственных возможностей Z1Z2 и зафиксированной кривой безразличия потребителя A.

Иначе говоря, линия Z1Z2 показывает различные наборы частного и общественного блага, которые могут быть произведены при полном использовании всех имеющихся ресурсов; кривая UA отражает множество наборов тех же благ, которые может выбрать потребитель A при фиксированном уровне полезности; линия C1C2 (разница между Z1Z2 и UA) показывает, что осталось потребителю B, т. е. какие наборы благ ему доступны.

Если предпочтения потребителя B заданы множеством кривых безразличия UB, то оптимальным для него будет набор E, где его полезность максимизируется при заданных потребительских возможностях. Поскольку кривая потребительских возможностей C1C2 получена как вертикальная разность между Z1Z2 и UA, то и ее наклон будет равен разности наклонов этих кривых. В свою очередь в точке оптимума E наклон кривой безразличия индивида B равен наклону C1C2. Таким образом, получаем, что предельная норма замены между частным (P) и общественным (G) благом для индивида B равна:

Отсюда получаем условие парето-оптимума для экономики с общественным благом:

или в случае множества потребителей: 

где I - число потребителей.

Исходя из аналогичных предположений, можно вывести условие оптимума по Парето при наличии общественных благ аналитически.

Пусть общее количество частных благ равно

где Pi - количество блага, потребленное i-тым индивидом.

В случае общественных благ:

G = Gi (i = 1,..., I),

где Gi - количество блага, потребленное i-тым индивидом.

Предпочтения индивидов заданы функциями полезности: Ui = Ui(Pi, G).                   

Предположим, что выполняется условие эффективности в производстве, и производственные возможности экономики могут быть описаны следующим уравнением кривой трансформации: F(P, G) = 0.          

Из всех решений (способов размещения ресурсов), удовлетворяющих этому уравнению, требуется выбрать такое решение, которое приведет к максимизации полезности данного потребителя (пусть это будет индивид B, как и в приведенном выше примере) при заданном уровне полезности всех остальных потребителей и заданных производственных возможностях экономики.