
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Алгебраические критерии устойчивости
Необходимое условие устойчивости
Характеристическое уравнение системы с помощью теоремы Виета может быть записано в виде
D(p) = aopn + a1pn-1 + a2pn-2 + ... + an = ao(p-p1)(p-p2)...(p-pn) = 0,
где p1, p2, ..., pn - корни этого уравнения. Если система устойчива, значит все корни левые, то есть вещественные части всех корней отрицательны, что можно записать какai = -|ai| < 0. Подставим их в уравнение:
a0
Перемножая комплексно сопряженные выражения, получим:
a0 После раскрытия скобок должно получиться выражение
a0
Так как в скобках нет ни одного отрицательного числа, то ни один из коэффициентов a0,a1,...,an не будет отрицательным. Поэтому необходимым условием устойчивости САУ является положительность всех коэффициентов характеристического уравнения: a0> 0, a1 > 0, ... , an > 0. В дальнейшем будем рассматривать только уравнения, где a0> 0. В противном случае уравнение домножается на -1. Рассмотренное условие является необходиным, но не достаточным условием. Необходимые и достаточные условия дают алгебраические критерии Рауса и Гурвица.
Критерий Рауса
Раус предложил критерий устойчивости САУ в виде алгоритма, по которому заполняется специальная таблица с использованием коэффициентов характеристического уравнения: 1) в первой строке записываются коэффициенты уравнения с четными индексами в порядке их возрастания; 2) во второй строке - с нечетными; 3) остальные элементы таблицы определяется по формуле: ck,i = ck+ 1,i - 2 - ri  4) Число строк таблицы Рауса на единицу больше порядка характеристического уравнения.
Критерий Рауса: для того, чтобы САУ была устойчива, необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса c11, c12, c13,... были положительными. Если это не выполняется, то система неустойчива, а количество правых корней равно числу перемен знака в первом столбце. Достоинство - критерий прост в использовании независимо от порядка характеристического уравнения. Он удобен для использования на ЭВМ. Его недостаток - малая наглядность, трудно судить о степени устойчивости системы, на сколько далеко отстоит она от границы устойчивости.
Критерий Гурвица
Гурвиц предложил другой критерий устойчивости. Из коэффициентов характеристического уравнения строится определитель Гурвица 1) по главной диагонали слева направо выставляются все коэффициенты характеристического уравнения от a1 до an; 2) от каждого элемента диагонали вверх и вниз достраиваются столбцы определителя так, чтобы индексы убывали сверху вниз; 3) на место коэффициентов с индексами меньше нуля или больше n ставятся нули. Критерий Гурвица: для того, чтобы САУ была устойчива, необходимо и достаточно, чтобы все n диагональных миноров определителя Гурвица были положительны. Эти миноры называются определителями Гурвица. Рассмотрим примеры применения критерия Гурвица: 1) n = 1 => уравнение динамики: a0p + a1 = 0. Определитель Гурвица: 2)n = 2 => уравнение динамики: a0p2 + a1p + a2 = 0. Определители Гурвица: 3) n = 3 =>уравнениединамики: a0p3 + a1p2 + a2p + a3 = 0. ОпределителиГурвица: Таким образом при n Критерий Гурвица применяют при n
Недостаток критерия Гурвица - малая наглядность. Достоинство - удобен для реализации на ЭВМ. Его часто используют для определения влияния одного из параметров САУ на ее устойчивость. Так равенство нулю главного определителя
Лекция 9. Частотные критерии устойчивости Это графоаналитические методы, позволяющие по виду частотных характеристик САУ судить об их устойчивости. Их общее достоинство в простой геометрической интерпретации, наглядности и в отсутствии ограничений на порядок дифференциального уравнения.
Принцип аргумента
Запишем характеристический полином САУ в виде
D(p) = a0
Егокорни pi =
гдеarg(pi) = arctg(
Каждый корень можно изобразить вектором на комплексной плоскости (рис.68а), тогда разность p - pi изобразится разностью векторов (рис.68б), где p- любое число. Еcли менять значение p произвольным образом, то конец вектора p - pi будет перемещаться по комплексно плоскости, а его начало будет оставаться неподвижным, так как pi - это конкретное неизменное значение. В частном случае, если на вход системы подавать гармонические колебания с различной частотой D(j
При этом концы векторов j Характеристический полином можно представить в виде
D(j где |D(j arg(D(j
Пусть из nкорней m - правые, а n - m - левые, тогда угол поворота вектора D(j
или при изменении
Отсюда вытекает правило: изменение аргумента вектора b при изменении частоты Это и есть принцип аргумента. Он положен в основе всех частотных критериев устойчивости. Мы рассмотрим два наиболее распространенных критерия: критерий Михайлова и критерий Найквиста.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 541. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (p + |a1|)
(p + |a1|)  2)
2) 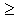 3 - номер строки, k - номер столбца.
3 - номер строки, k - номер столбца.
 по алгоритму:
по алгоритму: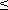 2 положительность коэффициентов характеристического уравнения является необходимым и достаточным условием устойчивости САУ. При n > 2 появляются дополнительные условия.
2 положительность коэффициентов характеристического уравнения является необходимым и достаточным условием устойчивости САУ. При n > 2 появляются дополнительные условия.

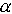 i + j
i + j  ,
, .
.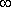 до +
до + 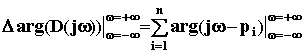 = (n - m)
= (n - m)  = (n - 2m)
= (n - 2m)