
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Инерционные звенья второго порядка
Его уравнение: T12p2y + T2py + y = ku. Передаточная функция:W(p) = Решение уравнения зависит от соотношения постоянных времени T1 и T2, которое определяет коэффициент затуханияr = Если r
T2p2 + 2rTp + 1 = T2
Такое звено можно разложить на два апериодических звена первого порядка, поэтому оно не является элементарным.
При r<1 корни полинома знаменателя W(p) комплексно сопряженные: p1,2 =
Дифференцирующее звено Различают идеальное и реальное дифференцирующие звенья. Уравнение динамики идеального звена: y(t) = Идеальное дифференцирующее звено реализовать невозможно, так как величина всплеска выходной величины при подаче на вход единичного ступенчатого воздействия всегда ограничена. На практике используют реальные дифференцирующие звенья, осуществляющие приближенное дифференцирование входного сигнала.  Его уравнение: Tpy + y = kTpu. Передаточная функция: W(p) = При малых Тзвено можно рассматривать как идеальное дифференцирующее. Переходную характеристики можно вывести с помощью формулы Хевисайда:
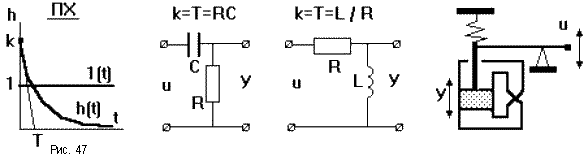
здесь p1 = - 1/T- корень характеристического уравненияD(p) = Tp + 1 = 0; кроме того, D’(p1) = T. При подаче на вход единичного ступенчатого воздействия выходная величина оказывается ограничена по величине и растянута во времени (рис.47). По переходной характеристике, имеющей вид экспоненты, можно определить передаточный коэффициентk и постоянную времени Т. Примерами таких звеньев могут являться четырехполюсник из сопротивления и емкости или сопротивления и индуктивности, демпфер и т.п. Дифференцирующие звенья являются главным средством, применяемым для улучшения динамических свойств САУ.
Кроме рассмотренных имеется еще ряд звеньев, на которых подробно останавливаться не будем. К ним можно отнести идеальное форсирующее звено (W(p) = Tp + 1, практически не реализуемо), реальное форсирующее звено (W(p) = Лекция 6. Частотные характеристики |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 632. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
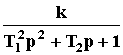 .
.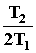 . Можно записать W(p) =
. Можно записать W(p) = 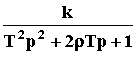 , где T = T1.
, где T = T1.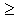 1, то знаменатель W(p) имеет два вещественных корня p1 и p2 и раскладывается на два сомножителя:
1, то знаменатель W(p) имеет два вещественных корня p1 и p2 и раскладывается на два сомножителя: (p - p1).(p - p2).
(p - p1).(p - p2).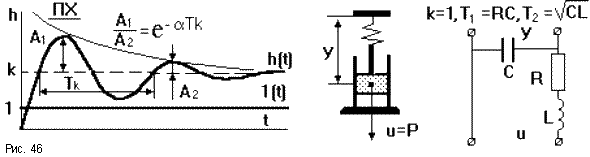
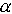 ± j
± j  . Переходная характеристика представляет собой выражение, характеризующее затухающий колебательный процесс с затуханием
. Переходная характеристика представляет собой выражение, характеризующее затухающий колебательный процесс с затуханием 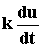 , или y = kpu. Здесь выходная величина пропорциональна скорости изменения входной величины. Передаточная функция: W(p) = kp. При k = 1 звено осуществляет чистое дифференцирование W(p) = p. Переходная характеристика:h(t) = k
, или y = kpu. Здесь выходная величина пропорциональна скорости изменения входной величины. Передаточная функция: W(p) = kp. При k = 1 звено осуществляет чистое дифференцирование W(p) = p. Переходная характеристика:h(t) = k 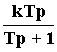 .
.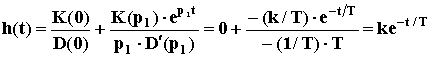 ,
,
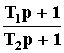 , при T1 >> T2), запаздывающее звено (W(p) = e - pT), воспроизводящее входное воздействие с запаздыванием по времени и другие.
, при T1 >> T2), запаздывающее звено (W(p) = e - pT), воспроизводящее входное воздействие с запаздыванием по времени и другие.