Основные определения и аксиомы статики

В статике изучаются условия равновесия и методы преобразования одних силовых систем в другие, эквивалентные данным.

Определение 1.

 Множество приложенных к телу сил называется                            системой сил.

Определение 2.

Две системы сил называются эквивалентными, если                             приложение каждой из них к одному и тому же                             покоящемуся свободному твёрдому телу приводит к                            одному и тому же движению:

Определение 3.  

Определение 4.   

Если система сил эквивалентна одной силе, то эта сила                            называется равнодействующей системы сил:

Аксиомы устанавливают простейшие правила действия над силами и системами сил.

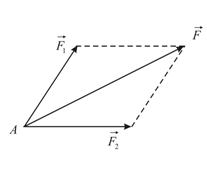
Аксиома 1.    

Две силы, приложенные в одной точке тела, эквивалентны одной силе, приложенной в той же точке и равной геометрической сумме этих сил

(Рис. 1.3).

	Рис. 1.3		Рис. 1.4

Аксиома 2.  

Не изменяя действия системы сил на тело, к ней можно добавить                   или от неё отнять уравновешенную систему сил.

Аксиома 3.  

Система двух сил, приложенных к абсолютно твёрдому телу,                  эквивалентна нулю тогда и только тогда, когда эти силы равны по                  модулю и действуют по одной прямой в противоположные стороны (Рис. 1.4).

Сформулированные аксиомы позволяют рассматривать систему сил, приложенную к абсолютно твёрдому телу, как систему скользящих векторов. В самом деле, аксиома 1 позволяет рассматривать силу как вектор. Покажем, что это вектор скользящий.

Рис.1.5

   Пусть в точке A абсолютно твёрдого тела приложена сила . Выберем на линии действия силы любую точку B, в которой приложим силы  и  (Рис.1.5), причём . На основании аксиом 1 и 2 получаем:                                                                                                                                                                                                                           так как   Но силы  и   также образуют уравновешенную систему сил и, следовательно, могут быть отброшены.

  Таким образом,