
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Смешанное произведение и его свойства.Определение. Смешанным произведением векторов а, в и с называется число, равное скалярному произведению вектораа на вектор, равный векторному произведению векторов в и с. Обозначается а*в*с или (а, в,с). Свойства смешанного произведения 1. Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е. (а х b )•с=(b х с)•а=(с ха)•b . Действительно, в этом случае не изменяется ни объем параллелепипеда, ни ориентация его ребер 2. Смешанное произведение не меняется при перемене местами знаков вкторного и скалярного умножения, т. е. (ахb)•с=а*(bx с). Действительно, (ахb )•с=±V и а•(b хс)=(b хс)•а=±V . Знак в правой части этих равенств берем один и тот же, так как тройки векторов а , b , с и b , с , а — одной ориентации. Следовательно, (a хb )•с=a (b хс). Это позволяет записывать смешанное произведение векторов (а х b )с в виде abc без знаков векторного, скалярного умножения. 3. Смешанное произведение меняет свой знак при перемене мест любых вух векторов-сомножителей, т. е. abc =-acb , abc=-bac , abc =-cba . Действительно, такая перестановка равносильна перестановке сомножителей в векторном произведении, меняющей у произведения знак. 4.Смешанное произведение ненулевых векторов а, b и сравно нулю огда и только тогда, когда они компланарны. Если abc =0 , то а, b и с— компланарны. Допустим, что это не так. Можно было бы построить параллелепипед с объемом V¹ 0. Но так как abc =±V , то получили бы, что abc¹0 . Это противоречит условию: abc =0. Обратно, пусть векторы а, b , с — компланарны. Тогда векторd =ахb будет перпендикулярен плоскости, в которой лежат векторы а, b ,с, и следовательно, d ^с. Поэтому d •с=0, т. е.abc =0. 
Уравнение прямой на плоскости (условие параллельности, перпендикулярности, угол между прямыми). общее уравнение прямой на плоскости:Ах+Ву+С=0,где С=-Ах₀-Bу₀ В зависимости от значений постоянных А,В и С возможны следующие частные случаи: • C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат • А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох • В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу • В = С = 0, А ≠0 – прямая совпадает с осью Оу • А = С = 0, В ≠0 – прямая совпадает с осью Ох Условие параллельности: Если прямые заданы уравнениями xcosα+ysinα-ρ=0(нормальное ур-ие прямой) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов: k1 = k2. Условие перпендикулярности: В случае, когда прямые заданы уравнениямиx cosα+y sinα-ρ=0 с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.
Угол между прямыми Углом междупрямыми A и B называется угол, на который надо повернуть первую прямую A вокруг точки пересечения этих прямых против движения часовой стрелки до совпадения ее со второй прямой B. Если две прямые заданы уравнениями с угловым коэффициентом. y=kx+m
Уравнение спроса.ур-е предложения.точкаравновес.цены Деление отрезка в заданном отношении. Если точка М(x; y) лежит на прямой, проходящей через две данные точки
Если точка М является серединой отрезка
Вывод ур-ияокр-ти. Если точка С - центр окружности, R - ее радиус, а M - произвольная точка окружности, то из определения окружности следует, что Пусть на плоскости задана прямоугольная декартова система координат и точка C(a;b)- центр окружности радиуса R. Пусть М(х;у) - произвольная точка этой окружности. Как известно, расстояние
или
Вывод ур-ия эллипса Эллипсом называетсягеометрическое место всехточек плоскости, сумма расстояний от которых до фокусов есть величинапостоянная, большая, чем расстояние между фокусами. Обозначим фокусы эллипса буквами Введем систему координат: Пусть М(х;у) - любая точка эллипса, тогда
Запишем характеристическое уравнение эллипса в координатной форме:
Преобразуем равенство:
Перенесем в левую часть равенства выражение, содержащее корень:
Так как а>с, то
Вывод ур-ия гиперболы Пусть расстояние между фокусами
где
Доказательство. Пусть M(х;у) -- текущая точка гиперболы (рис. 12.9).
Так как разность двух сторон треугольника меньше третьей стороны, то По условию, фокусы --
По определению гиперболы
Это уравнение запишем в виде
Обе части возведем в квадрат:
После приведения подобных членов и деления на 4, приходим к равенству
Опять обе части возведем в квадрат:
Раскрывая скобку и приводя подобные члены, получим
С учетом формулы
Разделим обе части уравнения на
Вывод уравнения параболы Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, Для вывода уравнения параболы выберем систему координат Оху так, чтобы ось Ох проходила через фокус F перпендикулярно директрисе в направлении от директрисы к F, а начало координат О расположим посередине между фокусом и директрисой (см. рис. 60). В выбранной системе фокус F имеет координаты Пусть М(х;у) — произвольная точка параболы. Соединим точку Μ с F. Проведем отрезок ΜΝ перпендикулярно директрисе. Согласно определению параболы MF = ΜΝ. По формуле расстояния между двумя точками находим:
Следовательно,
Возведя обе части уравнения в квадрат, получим
т. е.
Уравнение называется каноническим уравнением параболы. Парабола есть линия второго порядка.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 236. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |



 (
(  ,
, 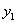 ) и
) и  (
(  ,
,  ), и дано отношение
), и дано отношение  , в котором точка М делит отрезок
, в котором точка М делит отрезок  , то координаты точки М определяются по формулам
, то координаты точки М определяются по формулам ,
,  .
. , то ее координаты определяются по формулам
, то ее координаты определяются по формулам ,
, 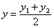 .
. . Последнее равенство есть характеристическое уравнение окружности радиуса R с центром в точке C.
. Последнее равенство есть характеристическое уравнение окружности радиуса R с центром в точке C. , поэтому уравнение можно записать так:
, поэтому уравнение можно записать так:


 и
и 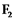 . Расстояние между ними - фокальное расстояние
. Расстояние между ними - фокальное расстояние  ,
,  и
и  . Если М(х;у) - произвольная точка эллипса, то по определению эллипса
. Если М(х;у) - произвольная точка эллипса, то по определению эллипса  - характеристическое уравнение эллипса .
- характеристическое уравнение эллипса . ,
,  и
и  . Тогда фокусами будут точки
. Тогда фокусами будут точки  и
и  .
.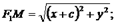











 . Пусть
. Пусть  , то
, то - каноническое уравнение эллипса .
- каноническое уравнение эллипса .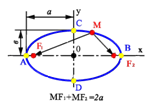
 и
и  гиперболы равно 2с , а абсолютная величина разности расстояний от точки гиперболы до фокусов равна
гиперболы равно 2с , а абсолютная величина разности расстояний от точки гиперболы до фокусов равна  . Тогда гипербола в выбранной выше системе координат имеет уравнение
. Тогда гипербола в выбранной выше системе координат имеет уравнение 


 , то есть
, то есть  ,
,  . В силу последнего неравенства вещественное число b , определяемое формулой
. В силу последнего неравенства вещественное число b , определяемое формулой  существует.
существует. ,
,  . По формуле
. По формуле  для случая плоскости получаем
для случая плоскости получаем






 уравнение принимает вид
уравнение принимает вид
 и получим уравнение
и получим уравнение 
 называемой директрисой. Расстояние от фокуса F до директрисы называется параметром параболы и обозначается через p (p > 0).
называемой директрисой. Расстояние от фокуса F до директрисы называется параметром параболы и обозначается через p (p > 0). , а уравнение директрисы имеет вид х=-р/2.
, а уравнение директрисы имеет вид х=-р/2.


