
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Системы линейных алгебраических уравненийРассмотрим СЛУ, у которой m уравнений и n неизвестных
-две системы линейных уравнений равносильны, если их множество решений совпадает -решением СЛУ является совокупность чисел от 1 до n, которое обращает каждое уравнение в тождество -СЛУ совместна, если имеет хотя бы 1 решение(опредеоенная;если больше1-го реш-неопредеенная), иначе несовместна
Решение СЛУ с помощью обратной матрицы. Запишем СЛУ в матричном виде:АХ=В(где А-матрица системы,сост.изкоэф.,стоящих пред неизвестными;В-матрица- столбец,состоящая из элементов,стоящи в правой части СЛАУ;Х-матрица-столбец,сотст-ая из неизвестных Х1,Х2,Х3) Для решения СЛАУ мат.мет: 1.выпишем матрицу системыА 2.найдем опр-ль а)если опр-ль =0,то решений нет б)если опр-ль≠0,то: 3.находим обратную матрицу Аˉ¹ к матрице системы 4.и т.к. справделиво АХ=В <=>Аˉ¹=АХ=Аˉ¹В<=>ЕХ=Аˉ¹В<=>Х=Аˉ¹В,то мы нашли матрицу-столбец Х,а след-но и неизвестные ПРИМЕР:
Решение: Запишем систему в матричной форме:
если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице А нужно было бы поставить нули. Обратную матрицу найдем по формуле:
Согласно формуле нужно найти обратную матрицуАˉ¹ и выполнить матричное умножение Аˉ¹b . Обратную матрицу найдем по формуле:
Сначала разбираемся с определителем:
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Т.о:
 Теперь записываем обратную матрицу:
А вот внести минус в матрицу в данном случае очень даже нужно, это, наоборот – упростит дальнейшие вычисления. Осталось провести матричное умножение
Решение СЛАУ по фор-амКрамера.
Метод джордна-гауса Решить методом Жордана-Гаусса систему уравнений:
Решение
Составим сначала соответствующую таблицу:
3. Заполняем вторую строку таблицы, используя формулу.
Получив таким образом коэффициенты bkl, запишем их в таблицу ниже от первой горизонтальной черточки. На пересечении второй строки и четвертого столбца этой таблицы стоит 1. Выберем ее за новый разрешающий элемент. Выполнив процедуру нахождения , получим окончательную таблицу коэффициентов 1. Разрешающим элементом изберем коэффициент при х3 в первом уравнении. Он единственный равняется единице (в рамке). 2. Разрешающая строка (первый) и разрешающий столбец сразу записываем в таблицу. 3. Заполняем вторую строку таблицы, используя формулу . Начнем с элемента b21. В предыдущей таблице находим элементы, которые стоят на пересечении первой и второй строк с первым и третьим столбцами и образовываем из них определитель: . Напомним, что произведение разрешающего элемента на тот, что стоит на его диагонали, всегда берется со знаком «+». Аналогично для нахождения b22 имеем определитель ; для ; . Дальше делаем проверку. Находим по аналогичному правилу элемент, который должны стоять во второй строке и в столбце ∑. Это будет . Записываем это значение в столбец contr. Вычисляем сумму элементов, которые стоят во второй строке к столбцу ∑: 0+0+1+1=2. Добытая сумма совпадает с соответствующим элементом столбца contr, поэтому коэффициенты второй строки таблицы найдено правильно. 5. Аналогично предыдущему находим элементы третьей строки: Получив таким образом коэффициенты bkl, запишем их в таблицу ниже от первой горизонтальной черточки. На пересечении второй строки и четвертого столбца этой таблицы стоит 1. Выберем ее за новый разрешающий элемент. Выполнив процедуру нахождения , получим окончательную таблицу коэффициентов
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 244. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

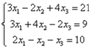
 ,где
,где

 ,где
,где  -транспонированная матрица алгебраических дополнений соответствующих элементов матрицы А .
-транспонированная матрица алгебраических дополнений соответствующих элементов матрицы А .



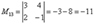
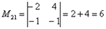





 -матрица миноров соответствующих элементов матрицы А.
-матрица миноров соответствующих элементов матрицы А. -матрица алг.доп.
-матрица алг.доп. -транспон.маталг.доп.
-транспон.маталг.доп.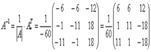




 образовываем из них определитель:.
образовываем из них определитель:.  определитель; для
определитель; для  ;
;  .
. . Записываем это значение в столбец contr.
. Записываем это значение в столбец contr. 