ОДНОКАНАЛЬНАЯ СМО С НЕОГРАНИЧЕННОЙ ОЧЕРЕДЬЮ

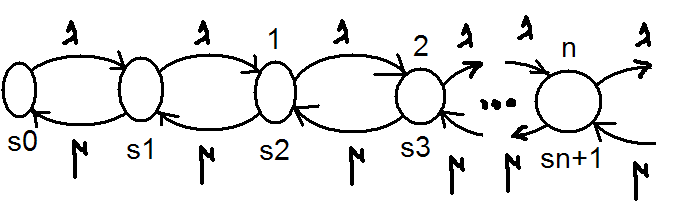
λ – интенсивность поступления заявок, Тобс = 1/ μ – время обслуживания.

S0 - система в режиме ожидания; S1 – канал занят, очередь пустая; S2 – канал занят, 1 заявка в очереди; S3 - …; Sn+1 – канал занят , n заявок в очереди;

р= λ/μ = λ* tобсл - приведенная интенсивность входного потока (кол-во заявок приходящих в систему в среднем за среднее время обслуживания одной заявки)

Р₀ - геометрическая прогрессия , сходимость будет если р <1 , т.е. очередь стабилизируется.

Если р >=1, то система не имеет стабильного режима, очередь удаляется в бесконечность.

р < 1 => λ < μ =>

Рn= Р_0* рⁿ - геометрическое распределение вероятностей. В системе установится стационарный режим.

A – число обслуженных заявок в единицу времени.

.

A xi – возможные значения случайной величины.

pi – вероятность принятия этих значений

М(числа заявок в канале) = Р₀*0+(1- Р₀)*1 =р.        

М – среднее число занятых каналов

Lоч – длина очереди. A = λ, λ - эквивалентна скорости.

(когда р<1)